2022-07-21 14:59:01 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәИAҲDҪМУэ
ОДХВҒнФҙЈәИAҲDҪМУэ
ПИҒнҝҙҝҙПВГжЯ@өАо},Ј¬Дг•юИзәОЗуҪв?
Аэо}
Ңў10ӮҖОеЗ§ГЧЩҗЕЬөДГыо~·ЦҪoТ»Ўў¶ю,ЎўИэ3ӮҖ°ајүЈ¬ЖдЦРТ»°аЦБЙЩ·ЦөҪ1ӮҖГыо~,Ј¬¶ю°аЦБЙЩ·ЦөҪ3ӮҖГыо~,ЎЈҶ–№ІУР¶аЙЩ·NІ»Н¬өД·ЦЕд·Ҫ·Ё?
A.28 B.36 C.45 D.51
ЎҫҪвОцЎҝ10ӮҖЩҗЕЬГыо~·ЦҪo3ӮҖ°аЈ¬Т»°аәН¶ю°аҫщУРТӘЗу,Ј¬„tҝЙПИҪoТ»°а·Ц1ӮҖ,Ј¬Ҫo¶ю°а·Ц3ӮҖ,Ј¬ҙЛ•rКЈУа10-1-3=6ӮҖГыо~Ј¬ФЩИҘ·ЦЕд,Ј¬УРТФПВИэоҗЗйӣrЈәўЩ·ЦҪoТ»ӮҖ°а,ЎЈТтУРИэӮҖ°ајү,Ј¬№І3·NЗйӣr;ўЪ·ЦҪoғЙӮҖ°аЎЈПИҸДИэӮҖ°ајүЦРЯxғЙӮҖ°ајүіцҒнКЗ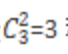 Зйӣr,Ј¬6ӮҖГыо~ҝЙ°ҙХХ(1Ј¬5)(2,Ј¬4)(3Ј¬3)(4,Ј¬2)(5,Ј¬1)·ЦөҪғЙӮҖ°ајүЦР,Ј¬№І5·NЗйӣrЈ¬№І3×5=15·NЗйӣr”ө(shЁҙ);ўЫ·ЦҪoИэӮҖ°а,ЎЈҝЙ°ҙХХ(1,Ј¬2,Ј¬3)(1Ј¬1,Ј¬4)(2Ј¬2,Ј¬2)·ЦҪoИэӮҖ°ајү,Ј¬ҝј‘]өҪКЗІ»Н¬°ајү,Ј¬ЛщТФ
Зйӣr,Ј¬6ӮҖГыо~ҝЙ°ҙХХ(1Ј¬5)(2,Ј¬4)(3Ј¬3)(4,Ј¬2)(5,Ј¬1)·ЦөҪғЙӮҖ°ајүЦР,Ј¬№І5·NЗйӣrЈ¬№І3×5=15·NЗйӣr”ө(shЁҙ);ўЫ·ЦҪoИэӮҖ°а,ЎЈҝЙ°ҙХХ(1,Ј¬2,Ј¬3)(1Ј¬1,Ј¬4)(2Ј¬2,Ј¬2)·ЦҪoИэӮҖ°ајү,Ј¬ҝј‘]өҪКЗІ»Н¬°ајү,Ј¬ЛщТФ ЧоәуЈ¬ИэоҗЗйӣr”ө(shЁҙ)ПајУ,Ј¬№І3+15+10=28·N,Ј¬ЯxAЎЈ
ЧоәуЈ¬ИэоҗЗйӣr”ө(shЁҙ)ПајУ,Ј¬№І3+15+10=28·N,Ј¬ЯxAЎЈ
ТФЙПҫНКЗҙујТФЪЧцо}•rіЈУГөДҪво}ЛјВ·,Ј¬Я@Т»ЛјВ·РиТӘЯMРР·ЦоҗУ‘Х“,Ј¬УГ•rйLЗТҝЙДЬҙжФЪЯzВ©»тЦШҸН(fЁҙ)УӢЛгөДЗйӣr,Ј¬ИЭТЧіцеeЎЈЯ@өАо}ДҝқMЧгБЛёф°еДЈРНөДК№УГ—lјю,Ј¬ОТӮғҝЙТФАыУГёф°еДЈРНҒнёьҝмёьңКҙ_ҢҰҙЛо}ЯMРРЗуҪвЎЈЧҢОТӮғТ»ЖрҢW(xuЁҰ)Б•(xЁӘ)Т»ПВёф°еДЈРН°Й!
Т»,Ўўёф°еДЈРНөДУӢЛ㹫КҪ
°СnӮҖПаН¬ФӘЛШ·ЦҪomӮҖІ»Н¬өДҢҰПу,Ј¬ГҝӮҖҢҰПуЦБЙЩ1ӮҖФӘЛШ,Ј¬№ІУР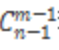
¶юЎўёф°еДЈРНөД‘Ә(yЁ©ng)УГ—lјю
АыУГёф°еДЈРНЗуҪв,Ј¬о}ДҝұШнҡН¬•rқMЧгТФПВ3ӮҖ—lјю:
1.ЛщТӘ·ЦөДФӘЛШұШнҡНкИ«ПаН¬;
2.ЛщТӘ·ЦөДФӘЛШұШнҡ·ЦНк,Ј¬ӣQІ»ФКФSУРКЈУа;
3.ГҝӮҖҢҰПуЦБЙЩ·ЦөҪ 1 ӮҖФӘЛШ,ЎЈ
ИэЎўёф°еДЈРНөД‘Ә(yЁ©ng)УГХ№Кҫ
Аэо}1
УР7үKПаН¬өДМЗ№ы,Ј¬·ЦҪo3ӮҖРЎЕуУСЈ¬ГҝИЛЦБЙЩ·ЦТ»үK,Ј¬УР¶аЙЩ·N·ЦЕд·Ҫ°ё?
ЎҫҪвОцЎҝЯ@өАо}ҫНқMЧгёф°еДЈРНөДЛщУР—lјюЈ¬ЛщТФҝЙТФЦұҪУМЧУГ№«КҪ
Аэо}2
УР7үKПаН¬өДМЗ№ы,Ј¬·ЦҪo3ӮҖРЎЕуУС,Ј¬РЎЬҠЦБЙЩ·ЦғЙүK,Ј¬ЖдУаГҝИЛЦБЙЩ·ЦТ»үKЈ¬УР¶аЙЩ·N·ЦЕд·Ҫ°ё?
ЎҫҪвОцЎҝҙЛо}І»қMЧгёф°еДЈРНөДөЪ3ӮҖ—lјюЈ¬ө«КЗҝЙТФНЁЯ^ЮD(zhuЁЈn)“QК№Ц®қMЧг,Ј¬ПИҪoРЎЬҠ·Ц1үK,Ј¬РЎЬҠЧғ?yЁӯu)йЦБЙЩ·ЦТ»үK,ЎЈКЈПВ6үKЈ¬·ЦҪo3ӮҖРЎЕуУСЗТГҝӮҖРЎЕуУСЦБЙЩ1үK,Ј¬АыУГ№«КҪ,Ј¬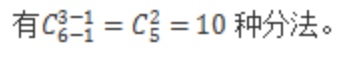
Аэо}3
УР7үKПаН¬өДМЗ№ы,Ј¬·ЦҪo3ӮҖРЎЕуУСЈ¬РЎгеҝЙТФІ»іФ,Ј¬ЖдУаГҝИЛЦБЙЩ·ЦТ»үK,Ј¬УР¶аЙЩ·N·ЦЕд·Ҫ°ё?
ЎҫҪвОцЎҝҙЛо}І»қMЧгёф°еДЈРНөДөЪ3ӮҖ—lјю,Ј¬ҝЙАыУГПИҪиәуЯҖФӯАнјЩФO(shЁЁ)°l(fЁЎ)·ЕХЯПИПтРЎгеҪи1үKМЗ№ыЈ¬ІўұЈЧCФЪ°l(fЁЎ)·ЕМЗ№ыөДЯ^іМЦР°СҪиЯ^ҒнөДМЗ№ыФЩ°l(fЁЎ)ЯҖ»ШИҘ,Ј¬ДЗГҙЯ@Ҷ–о}ҫНЧғіЙКЗ8үKМЗ№ы,Ј¬·ЦҪo3ӮҖРЎЕуУСЗТГҝИЛЦБЙЩДГ1үK,Ј¬АыУГ№«КҪЈ¬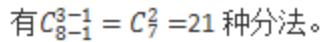

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБПЈ¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ