2021-12-09 14:24:47 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәәюұұ·ЦФә
ОДХВҒнФҙЈәәюұұ·ЦФә
№«ҝј”ө(shЁҙ)БҝкP(guЁЎn)ПөЦРУРР©оҗРНөДо}№«КҪ¶аЈ¬Чғ»Ҝ¶а,Ј¬ПлЗеіюөДХЖОХЯ@Р©оҗРНөДо}РиТӘҙуБҝөДҫ«БҰ,Ј¬ө«КЗУРТ»Р©оҗРНөДо}ПаҢҰҒнХf·Ҫ·ЁұИЭ^№М¶ЁЈ¬Э^ТЧХЖОХ,Ј¬ ұИИз№ӨіМҶ–о},Ј¬ ИЭівҶ–о} ЎЈ ҪсМмҫНҪoҙујТҪйҪBкP(guЁЎn)УЪИЭівҶ–о}өДПакP(guЁЎn)ғИ(nЁЁi)ИЭ ,ЎЈ
Т» ,Ўўо}РНМШьcЈәо}ёЙЦРіц¬F(xiЁӨn)ҝӮ?cЁЁ)Л”?shЁҙ)Ј¬ қMЧгA—lјюөДИЛ”ө(shЁҙ),Ј¬қMЧгB—lјюөДИЛ”ө(shЁҙ),Ј¬қMЧгC—lјюөДИЛ”ө(shЁҙ)Ј¬қMЧгAB—lјюөДИЛ”ө(shЁҙ),Ј¬қMЧгBCөДИЛ”ө(shЁҙ),Ј¬қMЧгACөДИЛ”ө(shЁҙ)Ј¬қMЧгABCөДИЛ”ө(shЁҙ),Ј¬ҝӮ?cЁЁ)Л”?shЁҙ)өИЯ@Р©БҝЦРөДІҝ·ЦБҝ,Ј¬ЗуЖдЦРДіӮҖОҙЦӘБҝЎЈ
¶ю,Ўў Ҫво}·Ҫ·Ё : ҝЙЦұҪУНЁЯ^№«КҪ»т®ӢҲDЗуҪв
¶ю јҜәПИݳ⹫КҪ Јә
A+B-A∩B=A∪B=ҝӮ”ө(shЁҙ)-¶јІ»қMЧгөДЗйӣr”ө(shЁҙ)
ИэјҜәПҳЛңКРН№«КҪЈә
A+B+C-A∩B-A∩C-B∩C+A∩B∩C=A∪B∪C=ҝӮ”ө(shЁҙ)-¶јІ»қMЧгөДЗйӣr”ө(shЁҙ)
ИэјҜәП·ЗҳЛңКРН№«КҪЈә
A+B+C-Ц»қMЧгғЙӮҖ—lјю-қMЧгИэӮҖ—lјю×2=A∪B∪C=ҝӮ”ө(shЁҙ)-¶јІ»қMЧгөДЗйӣr”ө(shЁҙ)
®”(dЁЎng)о}ёЙ ЦРЛщҪoөД”ө(shЁҙ)“ю(jЁҙ)І»Чг»тЛщЗуБҝ·ЗТФЙП№«КҪЦРөДБҝ•r,Ј¬ҝј‘]ЩxЦө·ЁЎЈ
Иэ,ЎўХжо}ёРЦӘ
ЎҫАэ 1 Ўҝ 240 ГыҢW(xuЁҰ)ЙъЦРҲуОД»ҜХnЭoҢ§(dЁЈo)°аөДЕcОҙҲуОД»ҜХnЭoҢ§(dЁЈo)°аөДИЛ”ө(shЁҙ)ұИКЗ 5:3 ,Ј¬ ҲуЛҮРg(shЁҙ) ЭoҢ§(dЁЈo)°аөДЕcОҙҲуЛҮРg(shЁҙ)ЭoҢ§(dЁЈo)°аөДИЛ”ө(shЁҙ)ұИКЗ 7:5 Ј¬ғЙоҗЭoҢ§(dЁЈo)°а¶јҲуөДУР 86 ИЛ,Ј¬„tғЙоҗЭoҢ§(dЁЈo)°а¶јӣ]УРҲуөДИЛ”ө(shЁҙ)КЗ?
A.36 ИЛ B.42 ИЛ
C.48 ИЛ D.54 ИЛ
Ўҫҙр°ёЎҝ A
ЎҫҪвОцЎҝ өЪТ»ІҪ,Ј¬ұҫо}ҝј Ій ¶ю јҜәП ИЭівҶ–о} Ј¬ҝЙЦұҪУАыУГ№«КҪ·ЁЗуҪв,ЎЈ
өЪ¶юІҪ,Ј¬ёщ“ю(jЁҙ)о}ёЙҝӮ?cЁЁ)Л”?shЁҙ)һй 2 40 ИЛ,Ј¬ Ҳу ОД»ҜХnЭoҢ§(dЁЈo)°аөДЕcОҙҲуОД»ҜХnЭoҢ§(dЁЈo)°аөДИЛ”ө(shЁҙ)ұИКЗ 5:3 Ј¬ ҲуЛҮРg(shЁҙ) ЭoҢ§(dЁЈo)°аөДЕcОҙҲуЛҮРg(shЁҙ)ЭoҢ§(dЁЈo)°аөДИЛ”ө(shЁҙ)ұИКЗ 7:5 ,�,ЈҝЙөГҲуОД»� Хn ЭoҢ§(dЁЈo)°аөДУР (ИЛ)Ј¬ Ҳу ЛҮРg(shЁҙ) ЭoҢ§(dЁЈo)°аөД УР (ИЛ),ЎЈ
өЪИэІҪ,Ј¬ФO(shЁЁ) ғЙоҗЭoҢ§(dЁЈo)°а¶јӣ]УРҲуөДИЛ”ө(shЁҙ) һй x Ј¬ЦұҪУҙъИ빫КҪ 1 50+140-86 = 240- x ,Ј¬ҪвөГ x= 36 ,ЎЈ
ТтҙЛЈ¬Яx“с A Яxн—,ЎЈ
ЙПо} КЗ ЦұҪУ АыУГҳЛңК№«КҪЗуҪвөД,Ј¬ҪУПВҒнОТӮғҝҙТ»ӮҖАыУГ·ЗҳЛңКРН№«КҪЗуҪвөД Аэо}ЎЈ
ЎҫАэ 2 Ўҝ ДіҢЈҳI(yЁЁ) 55 ГыН¬ҢW(xuЁҰ)¶јҲуГы…ўјУБЛҙуҢW(xuЁҰ)ЙъЙзҲF,Ј¬УР 35 ИЛ…ўјУБЛ»¬ұщЙз,Ј¬ 28 ИЛ…ўјУБЛ•ш·ЁЙзЈ¬ 31 ИЛ…ўјУБЛјӘЛыЙз,Ј¬ТФЙПИэӮҖЙзҲF¶ј…ўјУөДУР 6 ИЛ,Ј¬Ц»…ўјУТ»ӮҖЙзҲFөДУР ( ) ИЛЎЈ
A.22 B.29
C.33 D. 5
Ўҫҙр°ёЎҝ A
ЎҫҪвОцЎҝ өЪТ»ІҪ,Ј¬ұҫо}ҝјІйИэ јҜәПИЭівҶ–о} ,ЎЈ
өЪ¶юІҪЈ¬о}ёЙЗуЦ»…ўјУТ»ӮҖ ЙзҲF өД ИЛ”ө(shЁҙ),Ј¬УЙУЪӣ]УР¶јІ»…ўјУөД,Ј¬о}ёЙЛщЗујҙһйПВҲDЦРИэӮҖҲAЦРөДҝХ°ЧІҝ·Ц ЎЈ ҲDЦР ўЪ ұнКҫ Ц»қMЧг 2 ·NЗйӣrөДҝӮ ИЛ ”ө(shЁҙ) ,Ј¬ ўЫ ұнКҫ Н¬•rқMЧг 3 ·NЗйӣrөД ИЛ ”ө(shЁҙ) јҙ 6 ИЛ ,ЎЈ
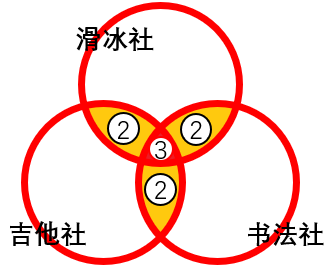
өЪИэІҪЈ¬ҙъИл·ЗИэјҜәПҳЛңКРН№«КҪ,Ј¬ 35+28+31 - ўЪ - 2 × 6= 55-0 ,Ј¬өГ ўЪ = 27 (ИЛ)Ј¬№КЛщЗуһй 55-27-6 = 22 (ИЛ),ЎЈ
ТтҙЛ,Ј¬Яx“с A Яxн—ЎЈ
ПаРЕҙујТНЁЯ^Я@ғЙөА о}ҝЙТФ ЗеіюөД БЛҪвөҪ,Ј¬лmИ» ИЭівҶ–о} ЦРҪoөД”ө(shЁҙ)“ю(jЁҙ)ұИЭ^¶а,Ј¬ө«КЗПаҢҰ ҒнХfЧц·Ё ұИЭ^№М¶Ё Ј¬ ДЬУГ№«КҪөДЦұҪУМЧУГ№«КҪ,Ј¬ І»ДЬЦұҪУНЁЯ^№«КҪөДҪY(jiЁҰ)әП®ӢҲDҪвӣQ ,ЎЈ ТтҙЛ ҙујТТ»¶ЁТӘңКҙ_өДУӣ‘ӣ№«КҪ,Ј¬ Я@ҳУІЕДЬ м`»оөДЯ\УГ өҪИЭівҶ–о} ЦР ЎЈ


ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә
ЙПТ»ЖӘЈә№«„Х(wЁҙ)ҶTРРңy”ө(shЁҙ)БҝкP(guЁЎn)ПөӮдҝјЦ®ЗЙҪв”ө(shЁҙ)БРҳӢ(gЁ°u)Фмо}РН
ПВТ»ЖӘЈә№«„Х(wЁҙ)ҶTРРңyӮдҝјЦ®К®ЧЦҪ»Іж·ЁЗЙҪв”ө(shЁҙ)БҝкP(guЁЎn)Пө

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ