2021-12-29 09:01:34 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁșBéT·ÖÔș
ÎÄŐÂíÔŽŁșBéT·ÖÔș
ŚșÎî}ÊÇ”(shšŽ)ÁżêP(gušĄn)Ï”ÖĐżŒČéîlÂÊ·ÇłŁžß”ÄÒ»îî}ĐÍŁŹĂżÄêŸùÓĐżŒČé,ŁŹ�,ŁżŒî}ĐÍÓĐ“ŚșÎÓ(jšŹ)Ë㔥ą“ŚșÎ(gš°u)Ôì”,ĄŁŚșÎî}Őûówëy¶ÈÖĐ”ÈÆ«žß,ŁŹÆäÖĐ“ŚșÎÓ(jšŹ)Ëă”ëy¶ÈßmÖĐŁŹ“ŚșÎ(gš°u)Ôì”ëy¶ÈÉÔžß,ĄŁ
ŚșÎÓ(jšŹ)Ëă·ÖéÒ(guš©)tŚșÎDĐÎÓ(jšŹ)ËăÒÔŒ°Č»Ò(guš©)tŚșÎDĐÎÓ(jšŹ)Ëă,ĄŁŠ(dušŹ)ÓÚÒ(guš©)tŚșÎDĐÎÓ(jšŹ)Ëăî}ŁŹĐèÒȘżŒÉúŠ(dušŹ)łŁÒ”ÄÆœĂæÒÔŒ°Áąów”ÄŚșÎč«ÊœÊìŸŐÆÎŐ,ŁŹČąÇÒÔÚżŒÔ”Äß^łÌÖĐ,ŁŹÓö”œłŁÒ”ÄŚșÎî}”Är(shšȘ)șòŁŹÄÜżìËٔķŽȘ(yš©ng)ß^í,ŁŹÇÒÖ±œÓÌŚÓĂč«ÊœŒŽżÉ,ĄŁ¶űŠ(dušŹ)ÓÚČ»Ò(guš©)tŚșÎDĐÎÓ(jšŹ)Ëăî}ŁŹœâQß@îŚșÎî}žü¶à”ÄÊÇČÉÓĂžîŃa(bšł)ÆœÒÆ”ÄËŒÏë,ŁŹÍšß^žîŃa(bšł)ÆœÒÆ”ÄÊÖ¶Î,ŁŹ°ŃČ»Ò(guš©)t”ÄŚșÎî}ȚD(zhušŁn)»ŻéÒ(guš©)t”ÄŚșÎî},ŁŹÔÙČÉÓĂÒ(guš©)t”ÄŚșÎč«ÊœÓ(jšŹ)ËăŒŽżÉ,ĄŁ
ŚșÎ(gš°u)Ôì”Äî}ŁŹÊÇÔÚŚșÎÓ(jšŹ)Ëă”Ä»ù”A(chšł)ÉÏŃĘ»Ż¶űí,ŁŹÒČŸÍÊÇÔÚî}ÖĐ,ŁŹ]ÓĐÖ±œÓœołöDĐÎșÍč«ÊœŁŹĐèÒȘżŒÉúŚÔŒșÈ„(gš°u)ÔìłöĆcî}ÒâÏàÆ„Ćä”ÄŚșÎDĐλòĐÔÙ|(zhšŹ),ŁŹÈ»șóÔÙÌÀí,ĄŁÆäĐèÒȘżŒÉúÒȘÓĐÒ»¶š”ÄżŐégÏëÏóÄÜÁŠŁŹÓĐÒ»¶š”Äëy¶È,ŁŹżŒÉúżÉÒÔÍšß^V·ș”ÄŸÁ(xšȘ),ŁŹÌážßŚÔŒș”Ä(gš°u)ÔìÄÜÁŠĄŁÏÂĂæÎÒíżŽÉ”ÀÀęî}Łș
ĄŸÀę1ĄżÒÒ”ŰÔÚŒŚ”Ű”ÄŐę|·œ26ǧÌÌ,ŁŹ±û”ŰÔÚŒŚ,ĄąÒÒÉ”ŰßBŸ”ı±·œŁŹÇÒĆcŒŚ,ĄąÒҔğàëx·Öeé24ǧÌșÍ10ǧÌ,ĄŁÒ»ĘvÜÄŒŚĄąÒÒÉ”ŰÖĐüc(dišŁn)λÖĂłö°l(fšĄ)ÏòŐę±±·œĐĐń,ŁŹÔÚœ(jš©ng)ß^ŒŚ±ûßBŸr(shšȘ),ŁŹĆc±û”Ű”ÄŸàëxÔÚÒÔÏÂÄÄ(gšš)·¶úÈ(nšši)?
A.Č»”œ8ǧÌ
B.8—9ǧÌ
C.9—10ǧÌ
D.10ǧÌÒÔÉÏ
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéÆœĂæŚșÎÓ(jšŹ)Ë㥣
”Ú¶țČœ,ŁŹÈçDŁș
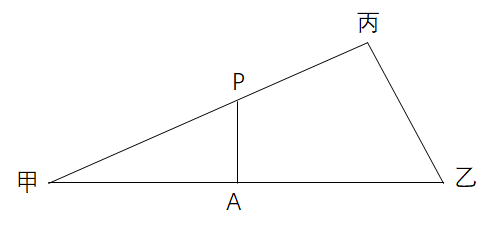
ŒŚÒÒ±ûÈęŐßêP(gušĄn)Ï”ÈçD,ŁŹAüc(dišŁn)éŒŚÒÒ”ÄÖĐüc(dišŁn)ŁŹPüc(dišŁn)éŒŚ±û”Äœ»üc(dišŁn),ĄŁÓÉlŒțżÉÖȘŒŚÒÒ=26ǧÌ,ŁŹŒŚ±û=24ǧÌŁŹ±ûÒÒ=10ǧÌ,ŁŹMŚăčŽčÉ”(shšŽ),ŁŹÒòŽËœÇ±ûéÖ±œÇĄŁžùț(jšŽ)î}Òâ,ŁŹPAŽčÖ±ŒŚÒÒËùÔÚÖ±Ÿ,ŁŹÒòŽËÉ(gšš)ÈęœÇĐÎÏàËÆŁŹÔO(shšš)Püc(dišŁn)”œŒŚ”ÄŸàëxéx,ŁŹtxĄĂ26=13:24,ŁŹżÉ”Ăx≈14.08ŁŹtPüc(dišŁn)”œ±û”ÄŸàëxé24-14.08=9.92,ŁŹÔÚ9—10ǧÌ֟ég,ĄŁ
ÒòŽËŁŹßxńCßxí(xiš€ng),ĄŁ
ĄŸÀę2ĄżÒ»(gšš)”ŚĂæ°ëœé10ÀćĂŚ,ŁŹów·eéV”Ä(shšȘ)ĐÄŐęAćFówÄŁŸßËźÆœ·ĆÖĂÔÚĆ_(tšąi)ĂæÉÏŁŹČąÓĂÒ»(gšš)ă@żŚ°ëœé2ÀćĂŚ”Äă@î^ÔÚÄŁŸßÉÏă@łöÒ»(gšš)ŽčÖ±ÓÚ”ŚĂæ”ĶŽÖ±ß_(dšą)”ŚČż,ĄŁÄÇĂŽÄŁŸßÊŁÓàČż·Ö”Äów·eÖÁÉÙéŁș
A.0.868V
B.0.876V
C.0.892V
D.0.896V
ĄŸŽđ°žĄżD
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéŚșÎî}ŁŹÙÓÚÁąówŚșÎî,ĄŁ
”Ú¶țČœ,ŁŹAćFów”Äów·eV=![]() πr²hŁŹ”ŚĂæ°ëœé10ÀćĂŚ,ŁŹtžßh(yušŁn)=
πr²hŁŹ”ŚĂæ°ëœé10ÀćĂŚ,ŁŹtžßh(yušŁn)=![]() ,ŁŹÏÈąă@żŚ”ÄĐÎ îœüËÆżŽéAÖùówŁŹžùț(jšŽ)AÖùówów·eπr²h,ŁŹă@żŚ°ëœé2ÀćĂŚ,ŁŹÆäów·eé
,ŁŹÏÈąă@żŚ”ÄĐÎ îœüËÆżŽéAÖùówŁŹžùț(jšŽ)AÖùówów·eπr²h,ŁŹă@żŚ°ëœé2ÀćĂŚ,ŁŹÆäów·eé![]() ŁŹÊŁÓàów·eé
ŁŹÊŁÓàów·eé![]() ,ĄŁ
,ĄŁ
”ÚÈęČœ,ŁŹă@żŚŚîÉÏ·œéAćFówŁŹžùț(jšŽ)ów·e±È”ÈÓÚß
éL±È(°ëœ±Èé2Łș10=1Łș5)”ÄÁą·œ,ŁŹżÉ”ĂŚîÉÏ·œAćFówów·eé![]() ,ŁŹžùț(jšŽ)AćFówów·eé
,ŁŹžùț(jšŽ)AćFówów·eé![]() πr²h,ŁŹżÉÖȘ֟ǰÓ(jšŹ)Ëăr(shšȘ)¶àpÈ„ÁË
πr²h,ŁŹżÉÖȘ֟ǰÓ(jšŹ)Ëăr(shšȘ)¶àpÈ„ÁË![]() πr²h”Äów·eŁŹÄÇĂŽÄŁŸßÊŁÓàČż·Ö”Äów·eÖÁÉÙé
πr²h”Äów·eŁŹÄÇĂŽÄŁŸßÊŁÓàČż·Ö”Äów·eÖÁÉÙé![]() =0.896V,ĄŁ
=0.896V,ĄŁ
ÒòŽË,ŁŹßxńDßxí(xiš€ng)ĄŁ
ŚșÎî}Ăżîî}Đ͔Ĝâî}·œ·šșÍČœóEČ»Ì«č̶š,ŁŹĐèÒȘżŒÉúÊìŸŐÆÎŐ»ù±Ÿ”ÄŚșÎč«Êœ,ŁŹČąÍšß^ŸÁ(xšȘ)ÌáÉęŠ(dušŹ)DĐΔÄĂôžĐ¶ÈĄŁœüÄêíŚșÎî}żŒČéîlÂÊłÊßfÔöÚ Ę,ŁŹÏŁÍûžśÎ»żŒÉúÒęÆđžß¶ÈÖŰÒ,ĄŁ

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș
ÉÏÒ»ÆȘŁșÊĄżŒĐĐyäżŒŁș”(shšŽ)ÁżêP(gušĄn)Ï”ÖźĐĐłÌî}
ÏÂÒ»ÆȘŁș2022Äêß|ÊĄżŒĐĐy”(shšŽ)ÁżêP(gušĄn)Ï”ÄăŒÒČĘÔÀï”ÄČĘòłÔá

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏ,ŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉżČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒŽđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé