2021-12-09 17:46:05 ЙЋе(wЈД)TПМдОW(wЈЃng) 
 ЮФеТэ(lЈЂi)дДЃККўББЗждК
ЮФеТэ(lЈЂi)дДЃККўББЗждК
еf(shuЈ)Ц№вЛдЊЖўДЮКЏЕ(shЈД)ЯраХДѓМвВЂВЛФАЩњ,ЃЌп@зЮвЛиЦ№СЫаЃ@r(shЈЊ)Йт,ЃЌКкАхЩЯЕФЮяООЭКУЯёr(shЈЊ)ЙтвЛгТ§Т§СїЪХ,ЁЃШчНёЮвИцeСЫаЃ@ЃЌЬЄЩЯСЫЙЋе(wЈД)TЕФПМдеїЭО,ЃЌдйДЮгів(jiЈЄn)СЫЪьЯЄгжФАЩњЕФвЛдЊЖўДЮКЏЕ(shЈД),ЁЃдкЙЋе(wЈД)TПМджаЕ(shЈД)СПъP(guЈЁn)ЯЕў(huЈЌ)ЩцМАЕНДЫюПМќc(diЈЃn)ЃЌЬиeЪЧдкН(jЈЉng)њ(jЈЌ)Рћ(rЈДn)(wЈЈn)ю}КЭзКЮ(wЈЈn)ю}жа,ЁЃЖјп@Щюю}аЭЪЧБиПМю}аЭ,ЃЌДѓМввЊЗ(wЈЇn)дњЗ(wЈЇn)ДђФУИпЗжЃЌФЧУДвЛдЊЖўДЮКЏЕ(shЈД)ЕФЊ(yЈЉng)гУОЭБиэеЦЮеРЮЙЬ,ЁЃ
ЁОW(xuЈІ)ЧАЂУЩЁП ЃКЪзЯШЮвэ(lЈЂi)ЛивЛЯТвЛдЊЖўДЮКЏЕ(shЈД)ЕФЛљБОжЊзR(shЈЊ)ЃЌПДПДЯТУцЕФКЏЕ(shЈД)DЯё,ЃЌФупФмЯыЦ№аЉЪВУДФи?
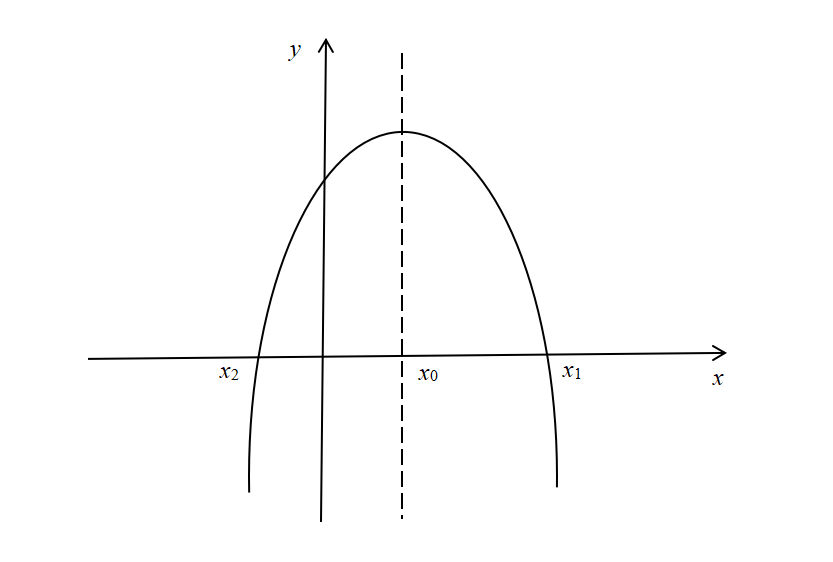
ФDЯёЩЯЮвПЩвдЕУГівдЯТз(gЈЈ)аХЯЂЃК
Ђй п@ЪЧвЛ(gЈЈ)щ_(kЈЁi)ПкЯђЯТЕФЮяО,ЃЌПЩвдШЁЕУзюДѓжЕЁЃ
Ђк x= x0 ЪЧКЏЕ(shЈД)ЕФІ(duЈЌ)ЗQнS ,ЃЌ дк x = x 0 ЬКЏЕ(shЈД)ШЁЕУзюДѓжЕ,ЁЃ
Ђл x1ЁЂx2ЗжeЪЧКЏЕ(shЈД)ЕФЩ(gЈЈ)Иљ,ЃЌЧв![]()
РћгУвдЩЯЛљБОаХЯЂ,ЃЌЮвПЩвдПьЫйЕУЕНаЮШчy=(x-m)(n-x)ЕФзюДѓжЕЃЌЗНЗЈШчЯТЃК
Ђй ЗжeСю x - m =0,ЃЌ n - x =0,ЃЌtДЫКЏЕ(shЈД)ЕФЩ(gЈЈ)ИљЗжeЪЧ m ЁЂ n,ЁЃ
Ђк Ў(dЈЁng)![]() r(shЈЊ),ЃЌКЏЕ(shЈД)ШЁЕУзюДѓжЕЁЃ
r(shЈЊ),ЃЌКЏЕ(shЈД)ШЁЕУзюДѓжЕЁЃ
ЁОеnЬУW(xuЈІ)С(xЈЊ)ЁП ЃКНгЯТэ(lЈЂi)ИаЪмвЛЯТецю}ЕФПМВщаЮЪН,ЃЌдкW(xuЈІ)С(xЈЊ)жаЂжЊзR(shЈЊ)Ш(nЈЈi)ЛЏгкаФ,ЁЃ
1ЁЂН(jЈЉng)њ(jЈЌ)Рћ(rЈДn)(wЈЈn)ю}Нy(tЈЏng)ЛIюЃКРћ(rЈДn)зюДѓЛЏ
ЁОР§ЁП ФГЩЬЦЗЕФпM(jЈЌn)иЮr(jiЈЄ)щ80дЊ,ЃЌфNЪлЮr(jiЈЄ)щ100дЊ,ЃЌУПЬьПЩЪлГі120Мў,ЁЃвбжЊфNЪлЮr(jiЈЄ)УПНЕЕЭ1дЊЃЌУПЬьПЩЖрЪлГі20Мў,ЁЃШєвЊ(shЈЊ)ЌF(xiЈЄn)дЩЬЦЗЕФфNЪлРћ(rЈДn)зюДѓЛЏ,ЃЌtфNЪлЮr(jiЈЄ)Њ(yЈЉng)НЕЕЭЕФН№ю~ЪЧ ЃК
A.5дЊ B.6дЊ
C.7дЊ D.8дЊ
ЁОД№АИЁП C
ЁОНтЮіЁПЕквЛВНЃЌБОю}ПМВщН(jЈЉng)њ(jЈЌ)Рћ(rЈДn)(wЈЈn)ю} жаЕФНy(tЈЏng)ЛIю ,ЁЃ
ЕкЖўВН,ЃЌдO(shЈЈ) фNЪлЮr(jiЈЄ) НЕЕЭЕФН№ю~щ x дЊЃЌМДНЕСЫ x (gЈЈ)1дЊ,ЃЌtУПМўРћ(rЈДn)з?yЈu)?00-80- x =20- x ,ЃЌ фNСПз?yЈu)?20+20 x ЁЃ Иљў(jЈД)ПРћ(rЈДn)=ЮМўРћ(rЈДn) × фNСП,ЃЌtПРћ(rЈДn)щ (20- x ) (120+20 x ) =20(20- x ) ( 6+ x ) ,ЁЃ ЗжeСю20- x =0ЃЌ6+ x =0,ЃЌЕУЕНДЫКЏЕ(shЈД)ЕФЩ(gЈЈ)ИљЗжeщ20КЭ-6,ЃЌФЧУДЎ(dЈЁng)![]() r(shЈЊ)ЃЌДЫКЏЕ(shЈД)ШЁЕУзюДѓжЕ ,ЁЃ вђДЫфNЪлЮr(jiЈЄ)Њ(yЈЉng)НЕЕЭ7дЊ,ЁЃ
r(shЈЊ)ЃЌДЫКЏЕ(shЈД)ШЁЕУзюДѓжЕ ,ЁЃ вђДЫфNЪлЮr(jiЈЄ)Њ(yЈЉng)НЕЕЭ7дЊ,ЁЃ
вђДЫЃЌБОю}пxё Cпxэ(xiЈЄng),ЁЃ
2,ЁЂзКЮ(wЈЈn)ю}г(jЈЌ)ЫуюЃКУцЗeзюДѓЛЏ
ЁО Р§ЁП ДхУёЬеФГГаАќвЛKщL(zhЈЃng)ЗНаЮЗNжВЕиЃЌЫћЂЕиЗжИюГЩШчDЫљЪОЕФ4(gЈЈ)аЁщL(zhЈЃng)ЗНаЮ,ЃЌдкA,ЁЂBЁЂC,ЁЂDЫФKщL(zhЈЃng)ЗНаЮЭСЕиЩЯЗжeЗNжВЮїЙЯ,ЁЂЛЈЩњЁЂЕиЙЯ,ЁЂЫЎЕО,ЁЃЦфжащL(zhЈЃng)ЗНаЮAЁЂB,ЁЂCЕФжмщL(zhЈЃng)ЗжeЪЧ20Уз,ЁЂ24УзЁЂ28Уз,ЃЌФЧУДщL(zhЈЃng)ЗНаЮDЕФзюДѓУцЗeЪЧЃК
A.42ЦНЗНУз B .49ЦНЗНУз
C.64ЦНЗНУз D .81ЦНЗНУз
ЁОД№АИЁП C
ЁОНтЮіЁП ЕквЛВН,ЃЌБОю}ПМВщзКЮ(wЈЈn)ю} жаЕФ ЦНУцзКЮ г(jЈЌ)Ыу ЁЃ
ЕкЖўВН,ЃЌдO(shЈЈ)AЕФщL(zhЈЃng)КЭЗжeщ x Уз ,ЁЂ y Уз ,ЃЌгЩщL(zhЈЃng)ЗНаЮAжмщL(zhЈЃng)щ20УзЃЌПЩЕУ x + y =10;гЩщL(zhЈЃng)ЗНаЮBжмщL(zhЈЃng) щ 24Уз,ЃЌЧвщL(zhЈЃng)ЗНаЮBХcщL(zhЈЃng)ЗНаЮAЕФщL(zhЈЃng)ЯрЭЌ,ЃЌПЩЕУBЕФщL(zhЈЃng)КЭЗжeщ x Уз ЁЂ y +2 Уз ;гЩщL(zhЈЃng)ЗНаЮCжмщL(zhЈЃng) щ 28Уз,ЃЌЧвщL(zhЈЃng)ЗНаЮCХcщL(zhЈЃng)ЗНаЮAЕФЯрЭЌ,ЃЌПЩЕУCЕФщL(zhЈЃng)КЭЗжeщ x +4 Уз ЁЂ y Уз ,ЁЃФЧУДщL(zhЈЃng)ЗНаЮDЕФУцЗeS=( x +4)( y +2)=( x +4)(10- x +2)=( x +4)(12- x ) ,ЃЌ ЗжeСю x +4 =0 ЃЌ12- x =0,ЃЌЕУЕНДЫКЏЕ(shЈД)ЕФЩ(gЈЈ)ИљЗжeЪЧ-4КЭ12,ЃЌФЧУДЎ(dЈЁng)![]() r(shЈЊ)ЃЌщL(zhЈЃng)ЗНаЮDЕФУцЗeзюДѓ,ЃЌ ДЫr(shЈЊ)S= ( 4+4)(12-4)= 64,ЃЌЙЪщL(zhЈЃng)ЗНаЮDЕФзюДѓУцЗeщ64ЦНЗНУзЁЃ
r(shЈЊ)ЃЌщL(zhЈЃng)ЗНаЮDЕФУцЗeзюДѓ,ЃЌ ДЫr(shЈЊ)S= ( 4+4)(12-4)= 64,ЃЌЙЪщL(zhЈЃng)ЗНаЮDЕФзюДѓУцЗeщ64ЦНЗНУзЁЃ
вђДЫ,ЃЌ БОю} пxёCпxэ(xiЈЄng),ЁЃ
ЁОеnКѓПНY(jiЈІ)ЁП гЩвдЩЯецю}ПЩвдПДГіЃЌвЛдЊЖўДЮКЏЕ(shЈД)юЕФПМВщжївЊМЏжадкзюДѓжЕЕФг(jЈЌ)Ыу,ЃЌгЩю}ИЩКмШнвзЕУЕНаЮШчy=(x-m)(n-x)ЕФБэп_(dЈЂ)ЪН,ЁЃМДЪЙаЮЪНЩЯгавЛаЉВюeЃЌЮввВПЩвдЭЈп^(guЈА)ЬсШЁЙЋвђЪНЕШЦфЫћЗНЪНЕУЕНy(tЈЏng)=(x-m)(n-x) ЕФаЮЪН,ЃЌШЛКѓСю![]() ЃЌДЫr(shЈЊ)КЏЕ(shЈД)ПЩвдШЁЕУзюДѓжЕ,ЃЌгЩДЫБуПЩвдК(jiЈЃn)ЛЏВЂПьЫйНтQ(wЈЈn)ю},ЁЃ
ЃЌДЫr(shЈЊ)КЏЕ(shЈД)ПЩвдШЁЕУзюДѓжЕ,ЃЌгЩДЫБуПЩвдК(jiЈЃn)ЛЏВЂПьЫйНтQ(wЈЈn)ю},ЁЃ

ЯръP(guЈЁn)Ш(nЈЈi)ШнЭЦЫ]ЃК
ЩЯвЛЦЊЃКЙЋе(wЈД)Tааy(cЈЈ)Е(shЈД)йYфПМИЩижЎШ§НЧаЮЯрЫЦдРэ
ЯТвЛЦЊЃК2022ФъЪЁПМпнХарфПМИЩижЎ?dЈЁng)?shЈД)СПюШчКЮПьЫйШыю}

ѓ(bЈЄo)УћlМў?
ЮЛпxё?
ЙPдПЦФП?
УцдЗНЪН?
......

 дкОПЭЗўЁС
дкОПЭЗўЁС

ќc(diЈЃn)єЫљашйYСЯ,ЃЌпДaюI(lЈЋng)ШЁ








еаПМЙЋИцПМдДѓОVТЮЛБэѓ(bЈЄo)УћШыПкЪ(zhЈГn)ПМзCДђгЁПМдr(shЈЊ)щgГЩП(jЈЉ)ВщдУцдУћЮфгУЙЋЪОПМдПьг
ѓ(bЈЄo)ПМСїГЬѓ(bЈЄo)ПМ(wЈЈn)Д№ѓ(bЈЄo)ПМlМўТФмНщНBеўВпЗЈв(guЈЉ)ѓ(bЈЄo)ПМЕ(shЈД)ў(jЈД)ЗжЮіvФъПМЧщ
Е(shЈД)СПъP(guЈЁn)ЯЕбдеZ(yЈГ)РэНтХарЭЦРэйYСЯЗжЮіГЃзR(shЈЊ)Харааy(cЈЈ)ММЧЩ