2021-05-26 14:52:45 č«ŐTżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁș°Č»Ő·ÖÔș
ÎÄŐÂíÔŽŁș°Č»Ő·ÖÔș
œüÄêíŁŹč«żŒÖДČșÎî}oŐÊÇî}ÁżßÊÇëy¶È¶ŒÓĐŽó·ùÌáÉę,ŁŹÓÈÆäÊÇÒ»Đ©żŽÆđíĘ^éÍës”ÄŚșÎî}Äż,ŁŹĐèÒȘßMĐĐŽóÁż”ÄÓË㣏”«żŒÉúÔÚëHżŒÔß^łÌÖĐÍùÍù]ÓĐłäŚă”ÄrégßMĐĐÔŒÓËă,ŁŹËùÒÔÔÚß@ÀïœoŽóŒÒœéœBÒ»·NżÉÒÔÓĐЧżs¶Ìœâî}ČœóE,ŁŹœ””ÍÓËăëy¶È”Ä·œ·š:±ÈÀę·šŁŹÏŁÍûÍšß^ß@ß ÎÄŐÂ,ŁŹżÉÒÔŚŽóŒÒówț”œ±ÈÀę·š”ÄĂîÓĂ,ĄŁ
ÔÚč«żŒÖĐ,ŁŹŚșÎî}ÖśÒȘ·ÖËÄîŁș
1.çRÏń¶ÌŸàî}
2.ÍŹ”Ś”Èžßî}
3.ÏàËÆDĐÎî}
4.čŽčɶšÀíî}ĄŁ
Śöî}rșòțÉæŒ°Ò»Đ©»ù±Ÿ”ÄĂæ·e,Ąąów·eč«Êœ,ĄŁÔÚÏàËÆDĐÎî}ÖĐŁŹÓĐŚÖŰÒȘ”ÄĐÔÙ|ĐèÒȘŽóŒÒÓ�,ĄŁ�
1.ÍŹÒ»î”ÄŐę¶àß ĐαˎËÏàËÆ,ŁŹËùÓĐAÏໄÏàËÆ;
2.ÏàËƱÈ=ŠȘß ”Ä±ÈŁŹ±ÈÈç,ŁŹÉA”İ뜱È,ĄąÖ±œ±È»òÖÜéL±ÈŸÍÊǶțŐßÏàËƱÈ;
3.Ăæ·e±È=ÏàËƱȔÄÆœ·œŁŹów·e±È=ÏàËƱȔÄÁą·œ,ĄŁ
łęÁËÏàËƱÈĆc±ÈÀęÓĐêPĂæ·e,Ąąów·e”ÄÇóœâÍùÍùÒČżÉÒÔÓñÈÀę·šżìËÙș»ŻÓË㣏ËùÓĐĐÎÈçA=B×CĐÎÊœ”Äč«Êœ,ŁŹ¶ŒÄÜßmźȘÓñÈÀę·š¶űÎÒÒ»°ă”ÄĂæ·e,Ąąów·eč«Êœ¶Œ»ù±Ÿ·ûșÏß@·NĐÎÊœ±ÈÈçŁșÆœĐĐËÄß ĐÎĂæ·e=”Ś×žß;Ò»°ăÖùówów·e=”ŚĂæ·eמß;Ò»°ăŚ”ówów·e=”ŚĂæ·eמß÷3ŁŹŠȘÉÏÊöč«Êœ,ŁŹŸÍÓĐŁșów·eĆc”ŚĂæ·e,Ąąžß·ÖełÉŐę±È;žßĆc”ŚĂæ·ełÉ·Ž±È
ĄŸÀ꥿(2020Äê°Č»ŐŁŹ)ÔÚÎĘÈŠœÇÌ¶Ń·Ć”ŸčÈ(ÈçD,ŁŹčȶŃéÒ»AćF”ÄËÄ·ÖÖźÒ»),ŁŹčÈ¶Ń”ŚČż”Ä»ĄéLé6ĂŚŁŹžßé2ĂŚ,ŁŹœ(jš©ng)ß^Ò»Òč°l(fšĄ)ŹF(xiš€n)čȶŃÔÚÖŰÁŠŚśÓĂÏ”ŚČż”Ä»ĄéLŚ?yšu)?ĂŚ,ŁŹÈôčÈ¶Ń”ÄčÈÁżČ»Ś,ŁŹÄÇĂŽŽËrčÈ¶Ń”ÄžßéŁș
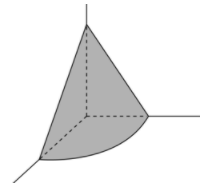
A.9/8ĂŚ B.8/9ĂŚ C.9/16ĂŚ D.4/9ĂŚ
ĄŸËŒÂ·Œ°œâî}ß^łÌĄż
żŽÒ“ÈçD”ŸÍżÉÒÔĆжšéŚșÎî}î},ŁŹ“ÈôčÈ¶Ń”ÄčÈÁżČ»ŚŁŹÄÇĂŽŽËrčÈ¶Ń”Äžßé”čÈÁżČ»Ś,ŁŹŸÍÊÇÖžów·eČ»ŚžßŚ?yšu)é¶àÉ�,ŁŹ¶űDœołö”ÄÊÇÒ»AćF”Ä1/4ŁŹÄÇĂŽ,ŁŹńRÉÏżÉÒÔÏ딜AćFów·eč«ÊœŁșów·e=”ŚĂæ·eמß÷3,ŁŹÈçčû°Žč«ÊœÏÈËăłöów·eŁŹÔÙËăłöșóí”Ä”ŚĂæ·eÀ^¶űÏàłę”Ă”œĐ”Ğß,ŁŹß@ˌ·ŚÔÈ»ÊÇżÉÒÔĐĐ”ĂÍš”Ä,ĄŁ”«ÊÇß@ÓÇóœâ±Ÿî}ŁŹČ»żÉ±ÜĂâ”ÄŸÍțŒÓŽóÓËăÁż,ŁŹów·eč«Êœ”ÄĐÎÊœÒÔŒ°“ów·eČ»Ś”ßÊDZÈĘ^ÈĘÒŚÏ딜±ÈÀę·š,ŁŹÄÇĂŽ,ŁŹŸÍżÉÒÔ±ÜĂâÓËăów·eÉőÖÁ”ŚĂæ·e¶ŒČ»ĐèÒȘÓË㣏ï@È»±ÈłŁÒ(guš©)ˌ·żìșܶà,ĄŁ
ÔÙżŽDĐÎ,ŁŹëmȻǰșóÉčȶŃČ»ÊÇÏàËÆAćFŁŹ”«ÊÇłöŹF(xiš€n)ÁË“A””ÄžĆÄîÏàêP”ÄżÉÒÔÏ딜“ËùÓĐ”ÄA¶ŒÏàËÆ”¶űčÈ¶Ń”ŚĂæ,ŁŹëmÈ»Č»ÊÇA,ŁŹ”«¶ŒÊÇ1/4AŁŹÉÈĐÎŚÔÈ»ÒČÊÇÏàËÆ”Ä,ĄŁÄÇĂŽÇ°șó”ŚĂæ·e”ıȟÍéËûÏàËƱȔÄÆœ·œ,ŁŹ¶űÏàËƱȟÍÊÇŠȘß ”ıÈÀꥣŠŐŐî}žÉ,ŁŹêPÓÚ”ŚĂæœołö”ĶŒÊÇ»ĄéL,ŁŹÒČŸÍÊÇŠȘ”Äß ŁŹËùÒÔ,ŁŹčȶŃÇ°șóÏàËƱÈéÇ°Łșșó=6:8=3:4,ŁŹtčȶŃÇ°șóĂæ·e±ÈéÇ°Łșșó=(3×3):(4×4)=9:16ĄŁÒòéčȶŃów·eČ»Ś,ŁŹËùÒÔžßșÍ”ŚĂæ·ełÉ·Ž±È,ŁŹËùÒÔŁŹčÈ¶Ńžß”Ä±ÈéÇ°Łșșó=16:9=(16×8)Łș(9÷8)=2Łș(9/8),ŁŹŒŽÔížßé2ĂŚ,ŁŹtŁŹșóížßé9/8ĂŚ,ŁŹčʱŸî}ßxA,ĄŁ
ß@Ò»î}ÖśÒȘÊÇœoŽóŒÒŐčÊŸÁËÏàËƱÈÔÚŸßówî}ÄżÖДČReșÍȘÓĂŁŹÒÔŒ°±ÈÀę·š”ÄÊčÓĂ,ĄŁß@î}Èçčû°ŽČżŸÍ°à”ÄßMĐĐÓËă,ŁŹÏÈÍšß^»ĄéLÇóÇ°șó”ŚĂæÉÈĐÎ°ëœĄąĂæ·e,ŁŹčâÍƧß^łÌčÀÓ¶ŒÒȘ»šșÜéLrég,ŁŹżŒörégÙFŁŹËùÒÔÒ»¶šÒȘWțŸCșÏȘÓĂËùWÖȘŚR,ĄŁÉÏÊöÖvœâżŽÆđí·±Ź,ŁŹ”«ÊÂÉÏÇ°ĂæÎÄŚÖČż·ÖČ»ß^ÊÇÔÚŽóÄXÖĐŸÍżÉÒÔÍêłÉ”ÄËŒŸSß^łÌŁŹëHŚöî}”Äß^łÌÖĐ,ŁŹÖ»ÒȘżÉÒÔÊìŸß\ÓñÈÀę·š,ŁŹÏàĐĆŽóŒÒÒ»¶šżÉÒÔÔÚșܶ̔ÄrégÈąß@îî}żìËÙÊŽ_”ÄÇóœâłöíĄŁ

ÏàêPÈÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț

óĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ