2021-05-26 14:27:57 ЙЋе(wЈД)TПМдОW(wЈЃng) 
 ЮФеТэдДЃКАВЛеЗждК
ЮФеТэдДЃКАВЛеЗждК

ѓ(bЈЄo)ПМю}НтЛѓ,ЃП
ЭЌW(xuЈІ)пДaзЩд

ХХСаНMКЯХcИХТЪю}ЪЧЕ(shЈД)W(xuЈІ)п\(yЈДn)Ыужа�,ЃПМЕФжиыyќc(diЈЃn)ЁЃКмЖрПМЩњІ(duЈЌ)п@вЛФЃKжЊзR(shЈЊ)ќc(diЈЃn)БШн^ФАЩњ,ЃЌгXЕУп@вЛФЃKГщЯѓ,ЃЌВЛжЊдѕУДЪ(zhЈГn)фЃЌБОЮФдМ(xЈЌ)НoДѓМвНщНBХХСаНMКЯХcИХТЪ�,ЃПМжЊзR(shЈЊ)ќc(diЈЃn),ЁЃ
Ў(dЈЁng)ЗћКЯlМўЕФЧщrБШн^ЩйЮвПЩвдЭЈп^УЖХeЕФЗНЗЈэНтQю}ЃЌБШШч2(gЈЈ)РЯдк3(gЈЈ)ЗПщgРяШЮпxЩщgзЁпM(jЈЌn)ШЅ,ЃЌвЊЧѓУПШЫзЁ1щgЙВ6ЗNЧщr;ЕЋЪЧШчЙћЗћКЯlМўЕФЧщrБШн^Жр,ЃЌШч5(gЈЈ)РЯдк10(gЈЈ)ЗПщgРяШЮпx5щgзЁпM(jЈЌn)ШЅЃЌУПШЫзЁ1щg,ЁЃп@r(shЈЊ)дйгУвЛвЛУЖХeЕФЗНЗЈ,ЃЌПМі(chЈЃng)ЩЯr(shЈЊ)щgЪЧВЛдЪдSЕФЁЃЫљвдЮвВЩгУХХСаНMКЯэг(jЈЌ)Е(shЈД),ЁЃЫќЪЧвЛЗNПЦW(xuЈІ)ЕФг(jЈЌ)Е(shЈД)ЙЄОп,ЃЌМШШЛЪЧг(jЈЌ)Е(shЈД)ФЧОЭў(huЈЌ)ЩцМАЕНМгЁЂp,ЁЂГЫ,ЁЂГ§ЁЃ
ХХСаНMКЯРягУЕФБШн^ЖрЕФЪЧМгЗЈКЭГЫЗЈ,ЁЃЗжюгУМгЗЈЁЂЗжВНгУГЫЗЈ,ЁЃХХСагУ“A”БэЪО,ЃЌНMКЯгУ“C”БэЪОЁЃНMКЯЪЧФn(gЈЈ)дЊЫижапxГіm(gЈЈ)ЗћКЯlМўЕФдЊЫи;ХХСаГ§СЫвЊпxпвЊІ(duЈЌ)пxГіэЕФдЊЫипM(jЈЌn)ааШЋХХСа,ЃЌЫљвдЃК
![]()
ЯТУцЮвЭЈп^ЛљЕA(chЈГ)ЕФХХСаНMКЯю}ФПэдЪіЃК
ЁОР§1ЁП(2019Фъј(guЈЎ)ПМ-Ек69ю}) ФГЮЮЛвЊЧѓТЙЄ ЂМг20еnr(shЈЊ)ОЩЯНЬг§еnГЬ,ЃЌАќКЌеўжЮРэе10еnr(shЈЊ)ЃЌЃI(yЈЈ)ММФм10еnr(shЈЊ),�,ЃПЩЙЉпxёЕФеўжЮРэееnЙВ8щTЃЌУПщT2еnr(shЈЊ);ПЩЙЉпxёЕФЃI(yЈЈ)ММФмеnЙВ10щT,ЃЌЦфжа2еnr(shЈЊ)ЕФга5щT,ЃЌ1еnr(shЈЊ)ЕФга5щTЁЃПЩпxёЕФеnГЬНMКЯЙВгаЖрЩйЗN?
A.5656 B.5600 C.1848 D.616
ЁОД№АИЁПA
ЁОНтЮіЁПБОю}ПМВщЛљЕA(chЈГ)ХХСаНMКЯЁЃеўжЮРэе10еnr(shЈЊ),ЁЂЃI(yЈЈ)ММФм10еnr(shЈЊ),ЃЌЕквЛВНеўжЮеnШЮпx5щTЃЌЕкЖўВНпxЃI(yЈЈ)ММФм10еnr(shЈЊ)ПЩЗжШ§юЂйпx5щT2еnr(shЈЊ)ЕФЂкпx4щT2еnr(shЈЊ)ЕФ,ЃЌ2щT1еnr(shЈЊ)ЕФЂлпx3щT2еnr(shЈЊ)ЕФ,ЃЌ4щT1еnr(shЈЊ)ЕФЁЃЗжВНгУГЫЗЈ,ЁЂЗжюгУМгЗЈ,ЃЌПЩЕУПЧщrщЃК![]()
ЙЪБОю}пxAЁЃ
ЁОР§2ЁП(2021ФъТ(liЈЂn)ПМ-АВЛеОэЕк24ю})ФГИпаЃщ_дO(shЈЈ)AюпxаоеnЫФщT,ЃЌBюпxаоеnШ§щT,ЃЌаЁЂФжаЙВпxШЁЫФщTеnГЬЃЌШєвЊЧѓЩюеnГЬИїжСЩйпxвЛщT,ЃЌtпxЗЈгаЃК
A.18ЗN B.22ЗN C.26ЗN D.34ЗN
ЁОД№АИЁПD
ЁОНтЮіЁПБОю}ПЩвдЯёР§1вЛгШЅЗжюЧѓНт,ЁЃвВПЩвдФцЯђЫМОS(ПЧщr-ВЛЗћКЯlМўЕФЧщr)ЃЌМД7щTеnГЬжаШЮпx4щTеnГЬpШЅЫФщTеnГЬШЋЪЧAюЕФЧщrЃК![]() ,ЁЃ
,ЁЃ
ХХСаНMКЯРяГ§СЫЛљЕA(chЈГ)ЕФю}аЭпгаЕфаЭЕФНтю}ММЧЩКЭЗНЗЈ,ЃЌАќРЈРІНЁЂВхПе,ЁЂѕАхЗЈЕШ,ЁЃ РІНЗЈЃКШчЙћю}ФПвЊЧѓвЛВПЗждЊЫиБиэдквЛЦ№ЃЌашвЊЯШЂвЊЧѓдквЛЦ№ЕФВПЗжвщвЛ(gЈЈ)ећѓw,ЃЌдйХcЦфЫћдЊЫивЛЦ№пM(jЈЌn)ааХХСа(зЂвтЃКРІНШ(nЈЈi)ВПЪЧЗёгаэађ
^(qЈБ)e);ВхПеЗЈЃКШчЙћю}ФПвЊЧѓвЛВПЗждЊЫиВЛФмдквЛЦ№,ЃЌtашвЊЯШХХСаЦфЫћжїѓwЃЌШЛКѓАбВЛФмдквЛЦ№ЕФдЊЫиВхПеЕНвбН(jЈЉng)ХХСаКУЕФдЊЫижащg(зЂвтЃКЩЖЫЪЧЗёЗтщ]);ѕАхЗЈЃКn(gЈЈ)ЯрЭЌЕФдЊЫиЗжГЩmНM,ЃЌвЊЧѓУП(gЈЈ)НMжСЩйга1(gЈЈ)дЊЫи,ЃЌПЩФмЕФЗNюЕ(shЈД)щ![]() ЁЃ
ЁЃ
ЁОР§3ЁП(2020ј(guЈЎ)ПМ-Ек62ю})ЗіиИЩВПФГШеашвЊзпдLДхШ(nЈЈi)6(gЈЈ)иРЇєМз,ЁЂвв,ЁЂБћЁЂЖЁ,ЁЂЮьКЭМК,ЁЃвбжЊМзКЭввЕФзпдLДЮађвЊЯррЃЌБћвЊдкЖЁжЎЧАзпдL,ЃЌЮьвЊдкБћжЎЧАзпдL,ЃЌМКжЛФмдкЕквЛ(gЈЈ)ЛђзюКѓвЛ(gЈЈ)зпдLЁЃзпдLэађгаЖрЩйЗNВЛЭЌЕФАВХХЗНЪН?
A.32 B.48 C.16 D.24
ЁОД№АИЁПC
ЁОНтЮіЁПЕквЛВН,ЃЌБОю}ПМВщХХСаНMКЯЕфаЭММЧЩРІН,ЁЂВхПе,ЁЃ
ЕкЖўВНЃЌЯШЂЮь,ЁЂБћ,ЁЂЖЁЯШКѓэађХХКУЃЌМКгаЩЗNпxё,ЃЌЂМзввРІНдквЛЦ№,ЃЌВхПеЕНжЎЧААВХХдЊЫиЫљаЮГЩЕФ4(gЈЈ)ПеРяЁЃМзввШ(nЈЈi)ВПЪЧгаэађ ^(qЈБ)eЕФ,ЁЃ
ЕкШ§ВН,ЃЌПЧщrщ2×4×2=16(ЗN)ЁЃ
ЙЪБОю}пxC,ЁЃ
ЁОР§4ЁП(2020ФъТ(liЈЂn)ПМ-АВЛеОэ13ю})ФГГЧЪавЛlЕРТЗЩЯга4(gЈЈ)ЪЎзжТЗПк,ЃЌУП(gЈЈ)ЪЎзжТЗПкжСЩйгавЛУћНЛЭЈ f(xiЈІ)ЙмTЃЌЌF(xiЈЄn)Ђ8(gЈЈ) f(xiЈІ)ЙмTУћю~ЗжХфЕНп@4(gЈЈ)ТЗПк,ЃЌtУП(gЈЈ)ТЗПк f(xiЈІ)ЙмTУћю~ЕФЗжХфЗНАИгаЃК
A. 35ЗN B. 70ЗN C. 96ЗN D. 114ЗN
ЁОД№АИЁПA
ЁОНтЮіЁПБОю}ПМВщѕАхЗЈ,ЁЃПЧщrщ![]() (ЗN),ЁЃЙЪБОю}пxA,ЁЃ
(ЗN),ЁЃЙЪБОю}пxA,ЁЃ
ДЫЭтХХСаНMКЯпН(jЈЉng)ГЃХcИХТЪю}НY(jiЈІ)КЯдквЛЦ№ПМЃЌР§ШчЃК
ЁОР§5ЁП(2012Фъј(guЈЎ)ПМ-Ек70ю})га5 І(duЈЌ)ЗђD ЂМгвЛі(chЈЃng)Лщбч,ЃЌЫћБЛАВХХдквЛ10 (gЈЈ)зљЮЛЕФAзРОЭВЭ,ЃЌЕЋЪЧЛщЖYВйоkепВЂВЛжЊЕРЫћБЫДЫжЎщgЕФъP(guЈЁn)ЯЕЃЌжЛЪЧыSC(jЈЉ)АВХХзљЮЛ,ЁЃ5 І(duЈЌ)ЗђDЧЁКУЖМБЛАВХХдквЛЦ№ЯррЖјзјЕФИХТЪЪЧЖрЩй?
A. дк1‰ЕН5‰жЎщg B. дк5‰ЕН1%жЎщg
C. ГЌп^1% D. ВЛГЌп^1‰
ЁОД№АИЁПA
ЁОНтЮіЁПБОю}ПМВщИХТЪ,ЁЃ
ЗНЗЈвЛЃКгУЗжВНИХТЪЧѓНтЁЃМйдO(shЈЈ)AзРэr(shЈЊ)сЗжeщ1-10Ь(hЈЄo)ЮЛ�,ЃЌF(xiЈЄn)дк1Ь(hЈЄo)ЮЛЩЯАВХХвЛ(gЈЈ)ШЫ,ЃЌШЮпxвЛШЫМДПЩЃЌИХТЪщ1;ЕкЖўВН,ЃЌДЫШЫЕФХфХМЯывЊКЭЦфзјвЛЦ№жЛФмзј2Ь(hЈЄo)Лђ10Ь(hЈЄo),ЃЌИХТЪщ![]() ;ЕкШ§ВНЃЌдкЪЃЯТЕФ8ШЫжаШЮпxвЛШЫзјдк3Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкЫФВНЃЌзјдк3Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк4Ь(hЈЄo)ЮЛЕФИХТЪщ
;ЕкШ§ВНЃЌдкЪЃЯТЕФ8ШЫжаШЮпxвЛШЫзјдк3Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкЫФВНЃЌзјдк3Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк4Ь(hЈЄo)ЮЛЕФИХТЪщ![]() ;ЕкЮхВН,ЃЌдкЪЃЯТЕФ6ШЫжаШЮпxвЛШЫзјдк5Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкСљВНЃЌзјдк5Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк6Ь(hЈЄo)ЮЛЕФИХТЪщ
;ЕкЮхВН,ЃЌдкЪЃЯТЕФ6ШЫжаШЮпxвЛШЫзјдк5Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкСљВНЃЌзјдк5Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк6Ь(hЈЄo)ЮЛЕФИХТЪщ![]() ;ЕкЦпВН,ЃЌдкЪЃЯТЕФ4ШЫжаШЮпxвЛШЫзјдк7Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкАЫВНЃЌзјдк7Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк8Ь(hЈЄo)ЮЛЕФИХТЪщ
;ЕкЦпВН,ЃЌдкЪЃЯТЕФ4ШЫжаШЮпxвЛШЫзјдк7Ь(hЈЄo)ЮЛ,ЃЌИХТЪщ1;ЕкАЫВНЃЌзјдк7Ь(hЈЄo)ЮЛЕФШЫЦфХфХМФмзјдк8Ь(hЈЄo)ЮЛЕФИХТЪщ![]() ЃЌЪЃЯТЕФЩ(gЈЈ)ШЫздШЛщвЛІ(duЈЌ)ЗђD,ЁЃЫљвдИХТЪщ
ЃЌЪЃЯТЕФЩ(gЈЈ)ШЫздШЛщвЛІ(duЈЌ)ЗђD,ЁЃЫљвдИХТЪщ![]() ,ЃЌТдДѓгкЧЇЗжжЎЖўЁЃ
,ЃЌТдДѓгкЧЇЗжжЎЖўЁЃ
ЗНЗЈЖўЃКПЩгУh(huЈЂn)аЮХХСаЕФЙЋЪНЧѓНт,ЁЃN(gЈЈ)ШЫХХГЩвЛШІКЭN-1(gЈЈ)ШЫХХГЩвЛСаЧщrЕ(shЈД)ЯрЭЌОљщ![]() ЗN,ЃЌЂ5І(duЈЌ)ЗђDРІНГЩ5(gЈЈ)ећѓwЃЌРІНЕФШ(nЈЈi)ВПгаэађ,ЁЃЫљвдЦфИХТЪщ
ЗN,ЃЌЂ5І(duЈЌ)ЗђDРІНГЩ5(gЈЈ)ећѓwЃЌРІНЕФШ(nЈЈi)ВПгаэађ,ЁЃЫљвдЦфИХТЪщ![]() ,ЁЃ
,ЁЃ
ЙЪБОю}пxAЁЃ
Г§СЫh(huЈЂn)аЮХХСа,ЃЌПМЩњпашвЊСЫНтхe(cuЈА)ЮЛХХСаЯръP(guЈЁn)жЊзR(shЈЊ)ќc(diЈЃn)ЃКгаn(gЈЈ)дЊЫиКЭn(gЈЈ)ЮЛжУ,ЃЌШчЙћвЊЧѓУП(gЈЈ)дЊЫиЕФЮЛжУХcдЊЫиБОЩэЕФађЬ(hЈЄo)ЖМВЛЭЌЃЌtn(gЈЈ)дЊЫиІ(duЈЌ)Њ(yЈЉng)ЕФХХСаЧщrЗжeщ,ЃЌD1=0ЗN,ЃЌD2=1ЗNЃЌD3=2ЗN,ЃЌD4=9ЗN,ЃЌD5=44ЗNЃЌ……Dn=(n-1)×(Dn-2+Dn-1)ЗN;ДЫЭтпашвЊжЊЕРЦНОљЗжНMЕФю}ФПвЊгЕУШЅжиЭ(fЈД),ЁЃ
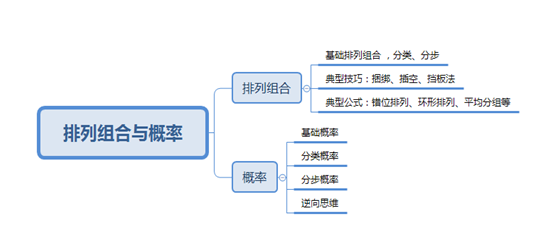
ИНЃКХХСаНMКЯХcИХТЪЫМОSЇ(dЈЃo)D
ЯЃЭћПМЩњФмЖрМгОС(xЈЊ),ЃЌИќЖрЯръP(guЈЁn)ПМдаХЯЂе(qЈЋng)МАr(shЈЊ)ъP(guЈЁn)зЂШADНЬг§ЙйОW(wЈЃng)!

ЯръP(guЈЁn)Ш(nЈЈi)ШнЭЦЫ]ЃК

йNаФПМЙЋПЭЗў

йNаФЃйПЭЗў
ЩЯвЛЦЊЃКааy(cЈЈ)фПМИЩиЃКдіщL(zhЈЃng)СПг(jЈЌ)Ыую}аЭНтЮі
ЯТвЛЦЊЃКааy(cЈЈ)фПМИЩиЃКзюжЕю}жЎ?dЈЁng)?shЈД)Са(gЈАu)дь

ѓ(bЈЄo)УћlМў?
ЮЛпxё?
ЙPдПЦФП?
УцдЗНЪН?
......

 дкОПЭЗўЁС
дкОПЭЗўЁС

ќc(diЈЃn)єЫљашйYСЯЃЌпДaюI(lЈЋng)ШЁ








еаПМЙЋИцПМдДѓОVТЮЛБэѓ(bЈЄo)УћШыПкЪ(zhЈГn)ПМзCДђгЁПМдr(shЈЊ)щgГЩП(jЈЉ)ВщдУцдУћЮфгУЙЋЪОПМдПьг
ѓ(bЈЄo)ПМСїГЬѓ(bЈЄo)ПМД№ѓ(bЈЄo)ПМlМўТФмНщНBеўВпЗЈв(guЈЉ)ѓ(bЈЄo)ПМЕ(shЈД)ў(jЈД)ЗжЮіvФъПМЧщ