2022-01-17 10:09:06 č«ŐTżŒÔŸW 
 ÎÄŐÂíÔŽŁșșț±±·ÖÔș
ÎÄŐÂíÔŽŁșșț±±·ÖÔș
ŚșÎî}ĆcÆäËûîĐÍî}ësôÛ,ŁŹżŽËÆÍës,ŁŹtŐÆÎŐłŁżŒ”ÄîĐÍ,ŁŹ°ŃÎŐ·œ·šÒČŸÍČ»ëyÁË,ŁŹÄÇĂŽœńÌìÖśÒȘœéœBÈę·NżŒîlžßŁŹÌŚÂ·,ŁŹĘ^ÈĘÒŚŐÆÎŐ”Äî}ĐÍ,ĄŁ
Ò»ĄąŚșÎ+œúÀûŚîÖ”î}
ŚșÎĆcœúÀûŚîÖ”î},ŁŹ±MčÜŸCșÏÁËÉî}ĐÍ,ŁŹ”«î}Äżëy¶È”ÍŁŹÌŚÂ·č̶š,ŁŹÖ»ĐèÉÔŒÓżœY,ŁŹșóÀm(xšŽ)ß@·NîĐÍî}Äż¶ŒżÉÒÔËÙœâĄŁ
ĄŸÀ꥿ijÉÌÆ·”ÄßMŰÎré80ÔȘ,ŁŹäNÊÛÎré100ÔȘ,ŁŹĂżÌìżÉÊÛłö120Œț,ŁŹÒŃÖȘäNÊÛÎrĂżœ””Í1ÔȘŁŹĂżÌìżÉ¶àÊÛłö20Œț,ĄŁÈôÒȘŹF(xiš€n)ÔÉÌÆ·”ÄäNÊÛÀûŚîŽó»Ż,ŁŹtäNÊÛÎrȘœ””͔Ĝđî~ÊÇŁș
A.5ÔȘ
B.6ÔȘ
C.7ÔȘ
D.8ÔȘ
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»ČœŁŹ±Ÿî}żŒČéœúÀûî},ĄŁ
”Ú¶țČœ,ŁŹÔOżÀûéyÔȘŁŹœ””͔Ĝđî~énÔȘ,ŁŹŒŽœ”ÁËn1ÔȘ,ŁŹtĂżŒțÀûŚ?yšu)?00-80-n=20-nĄŁžùț(jšŽ)żÀû=ÎÀûäNÁż,ŁŹty=(20-n)×(120+20n),ŁŹß@ÊÇÒ»Ò»ÔȘ¶țŽÎ·œłÌŁŹșŻ”(shšŽ)DÏńÊÇÒ»é_żÚÏòÏ”ÄÎïŸ,ŁŹÄǔóöÉÁăüc,ŁŹŠȘÖĐégÖ””Äy±ăÊÇŚîžßücŁŹÒČŸÍÊÇÎÒËùÇó”ÄÀûŚîŽó»Ż,ĄŁ
”ÚÈęČœ,ŁŹ20-n=0ŁŹn=20;120+20n=0,ŁŹn=-6,ŁŹtÖĐégÖ”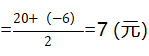 ĄŁ
ĄŁ
ÒòŽË,ŁŹßxńCßxí,ĄŁ
¶țĄąŚșÎ+ĐĐłÌî}
ĐĐłÌî}ÊÇșܶàÍŹWÔÚäżŒß^łÌÖĐÓX”Ăëy¶ÈĘ^žß”Äî}ĐÍ,ŁŹÔÙœYșÏŚșÎ,ŁŹÄÇŸÍÍû¶ű sČœÁËŁŹÆäČ»È»,ŁŹĆcŚșÎœYșÏ”ÄĐĐłÌî}ÍšłŁ¶ŒșÜșÎ,ŁŹżŒČìÉÔëyÒ»ücÒČŸÍÊÇß\ÓñÈÀę·šŁŹÀûÓĂÄłÒ»ÁżČ»Ś,ŁŹÆäËûÉÁżłÉŐę±È»ò·Ž±È”ÄêPϔȄœâî}ĄŁ
ĄŸÀ꥿ȿê Ç°ÉÚŐŸ”ÄÀŚß_±O(jišĄn)y·¶úé100ǧÌ,ĄŁÄłÈŐÇ°ÉÚŐŸÉy”œŐę|Æ«±±30°100ǧÌÌ,ŁŹÒ»ŒÜżÉÒÉoÈËCŐęòËÙÏòŐęÎś·œÏòïwĐĐĄŁÇ°ÉÚŐŸÍšÖȘŐęÄÏ·œÏò150Ç§ĂŚÌ”ÄČżê ÁąŒŽÏòŐę±±·œÏò°l(fšĄ)ÉäoÈËCrœŰ,ŁŹòËÙïwĐĐÒ»¶Îrégșó,ŁŹŐęșĂÔÚÄłücĆcżÉÒÉoÈËCÏàÓö,ĄŁÎÒ·œoÈËCËÙ¶ÈÊÇżÉÒÉoÈËC”ĶàÉÙ±¶?
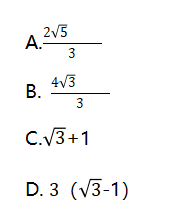
ĄŸŽđ°žĄżB
ĄŸœâÎöĄż”ÚÒ»ČœŁŹ±Ÿî}żŒČéŚșÎî},ĄŁ
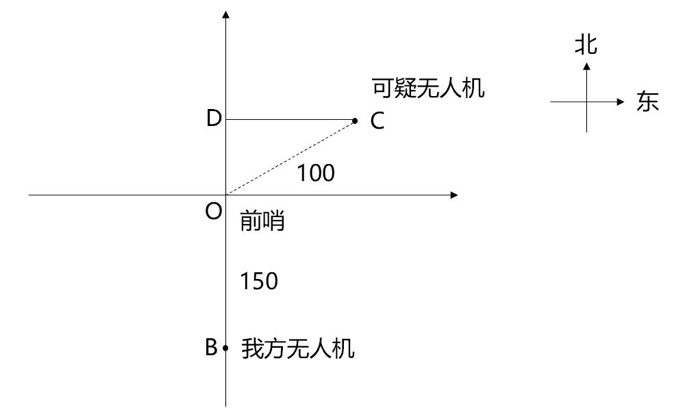
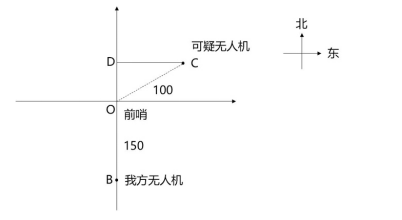
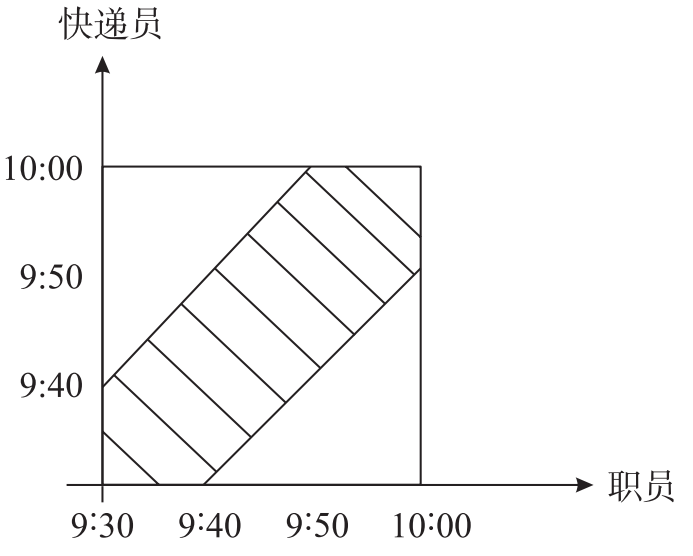
”Ú¶țČœ,ŁŹžùț(jšŽ)î}Ò⣏ÎÒ·œoÈËCĆcżÉÒÉoÈËCÏàÓör,ŁŹïwĐĐŸàëx,ŁŹÈçDËùÊŸŁș
ÎÒ·œoÈËC”ÄïwĐĐŸàëxéBD=BO+ODŁŹżÉÒÉoÈËC”ÄïwĐĐŸàëxéCD,ŁŹœYșÏÖ±œÇÈęœÇĐΔÄÌŰĐÔ,ŁŹOD=OC/2=50ŁŹCD=![]() ,ŁŹtBD=200,ĄŁœYșϱÈÀęĐĐłÌŁșrégÒ»¶š”ÄrșòŁŹËÙ¶ÈĆc·łÌłÊŐę±È,ŁŹtÎÒ·œoÈËC”ÄËÙ¶ÈŁșżÉÒÉoÈËC”ÄËÙ¶È
,ŁŹtBD=200,ĄŁœYșϱÈÀęĐĐłÌŁșrégÒ»¶š”ÄrșòŁŹËÙ¶ÈĆc·łÌłÊŐę±È,ŁŹtÎÒ·œoÈËC”ÄËÙ¶ÈŁșżÉÒÉoÈËC”ÄËÙ¶È
ÒòŽË,ŁŹßxńBßxíĄŁ
Èę,ĄąŚșÎ+žĆÂÊî}
žĆÂÊŚșő·êżŒ±Űłö,ŁŹœüŚÄêî}ĐÍÉÏÒČÊÇ°l(fšĄ)ÉúÁËÒ»Đ©Ś»ŻŁŹÓÈÆäÊÇœüÉÄêÌŰeÏČgĆcŚșÎî}œYșÏÔÚÒ»ÆđżŒČì,ŁŹÒČŸÍÊÇŚșΞĆÂÊî},ŁŹÏà±ÈÓÚ֟ǰżŒČì”Äśœy(tšŻng)žĆÂÊíÖvŁŹÆäëy¶ÈÊÇœ””ÍÁËÒ»Đ©,ŁŹ±ÈÈçÏÂĂæß@”Àî}ÄżŁș
ĄŸÀ꥿ijč«ËŸÂTîAŒsÄłżìßfTÉÏÎç9üc30·Ö”œ10ücÔÚč«ËŸŽóÇÇ°ÈĄŒț,ŁŹŒÙÔOÉÈËŸùÔÚß@¶ÎrégÈ”œß_ŁŹÇÒÔÚß@¶Îrég”œß_”ÄžĆÂÊÏà”È,ĄŁŒs¶šÏÈ”œŐß”Èșó”œŐß10·Öç,ŁŹß^rœ»ÒŚÈĄÏû�,ŁżìßfTÈĄŒțłÉ芔ĞĆÂÊéŁș
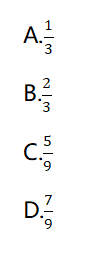
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéžĆÂÊî}ŁŹÓĂDÏń·šœâî},ĄŁ
”Ú¶țČœ,ŁŹÔOč«ËŸÂT”œß_régéxŁŹżìßfT”œß_régéY,ŁŹÉÈËÏàČîČ»łŹß^10·Ö甜ß_żÉœ»ÒŚłÉčŠ,ŁŹtżÉ”Ă”œ|X-Y|ŁŹżÉÀLÖÆłöÆäșŻ”(shšŽ)DÏńÈçÏÂŁș
ÄÇĂŽêÓ°ÊÇÈĄŒțłÉ芔ÄČż·ÖŁŹtÆäŐŒ±Èé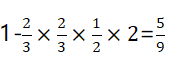
ÒòŽË,ŁŹßxńCßxí,ĄŁ
ÒÔÉÏÊÇœoŽóŒÒżœYÁËÈę·NÏČgĆcŚșÎœYșÏ”Äî}ĐÍŁŹ¶ŒÊÇ“ŒÀÏ»ą”,ŁŹżŽÖűșÜÈË,ŁŹtșÜșÎŁŹËùÒÔŽóŒÒĐèÒȘÔÚÆœłŁŸÁÖĐ,ŁŹČ»ÒȘһζ”ÄËąî},ŁŹ¶űÊÇÒȘÈ„¶àżœY·ÖÎöî}Äż”ÄÚ ĘŁŹß@ÓČĆÄÜòÓĐáŠĐԔğÁ,ŁŹČĆÄÜ“ŸíËÀeÈË,ŁŹłÉŸÍŚÔŒș”ĄŁ

ÏàêPÈÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț

óĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ