2021-11-12 13:29:43 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәәюұұ·ЦФә
ОДХВҒнФҙЈәәюұұ·ЦФә

ҲуҝјҶ–о}Ҫв»у,Јҝ
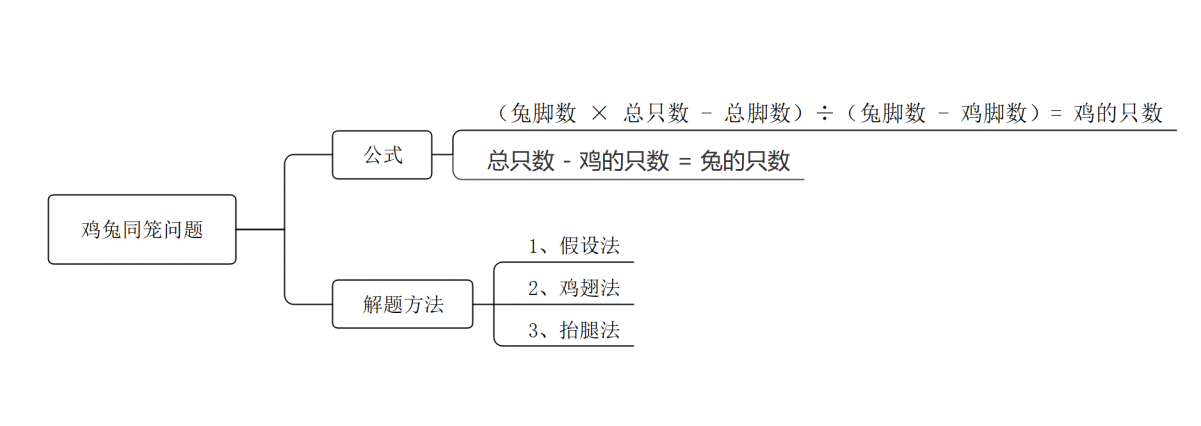
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

лuНГН¬»\КЗЦРҮш№ЕҙъөД”ө(shЁҙ)ҢW(xuЁҰ)Гыо}Ц®Т» ,Ј¬ФзФЪ Ў¶ ҢOЧУЛгҪӣ(jЁ©ng) Ў· ЦРҫНУРБЛЯ@ҳУөД”ўКцЈәҪсУРпфНГН¬»\Ј¬ЙПУРИэК®Оео^,Ј¬ПВУРҫЕК®ЛДЧг,Ј¬Ҷ–пфНГёчҺЧәОЈҝ ТвЛјКЗУРлuәННГЧУФЪТ»ӮҖ»\ЧУАп,Ј¬ДЬҝҙөҪУР35ӮҖо^әН94 —lНИ,Ј¬Ҷ–УРлuәННГЧУёчҺЧЦ»ЎЈ Я@ӮҖҶ–о}ұҫЩ|(zhЁ¬)ЙПКЗТ»·N¶юФӘ·ҪіМ,Ј¬о}ФO(shЁЁ)—lјю°ьАЁБЛІ»Н¬”ө(shЁҙ)БҝөДо^әННИ,Ј¬ДЗЯ@·NҶ–о}ИзәОҝмЛЩҪвӣQДШЈҝ Я@АпОТӮғІЙУГјЩФO(shЁЁ)·Ё,ЎЈјЩФO(shЁЁ)35ӮҖо^И«Іҝ¶јКЗНГЧУ,Ј¬ДЗГҙ‘Ә(yЁ©ng)Ф“УР35×4=140—lНИЎЈө«КЗ¬F(xiЁӨn)ФЪҢҚлHЦ»УР94 —lНИ,Ј¬јЩФO(shЁЁ)ұИҢҚлH¶аБЛ46 —lНИ,ЎЈТ»Ц»лuЧғіЙТ»Ц»НГЧУ•ю¶аіц2—lНИЈ¬ДЗГҙ¶аіцөД46 —lНИ,Ј¬‘Ә(yЁ©ng)Ф“КЗ46 ÷ 2 = 23 Ц»лuФЪјЩФO(shЁЁ)өД•rәтЧғіЙБЛНГЧУ,Ј¬ТтҙЛКЗУР23 Ц»лuЈ¬¶шНГЧУ”ө(shЁҙ)БҝҫНКЗ35-23=12Ц»,ЎЈ
УЙҙЛОТӮғҢҰлuНГН¬»\Ҷ–о}ЧчіцТэЙк,Ј¬®”(dЁЎng)о}ДҝЦРіц¬F(xiЁӨn)ғЙӮҖІ»Н¬өДҢҰПу ,Ј¬¶шЯ@ғЙӮҖІ»Н¬өДҢҰПуУЦН¬•r“нУРғЙ·N І»Н¬МШРФ•rЈ¬ОТӮғҫНҝЙТФК№УГлuНГН¬»\өДЛјПлҒнҪвӣQҶ–о},ЎЈИзТФПВғЙөААэо},ЎЈ
ЎҫХжо}1Ўҝ ДіЩҗКВҢҚРР·e·ЦЩҗЦЖЈ¬«@„Щ·e5·Ц,Ј¬ҙтЖҪ·e2·Ц,Ј¬К§”ЎҝЫ1·ЦЎЈТСЦӘРЎЭxФЪ20Ҳц·e·ЦЩҗәу·e61·ЦЗТУР3ҲцұИЩҗҙтЖҪ,Ј¬ДЗГҙРЎЭxөД„ЩВКһй ЈЁ Ј© Јә
A. 48% B. 55%
C. 60% D. 75%
Ўҫҙр°ёЎҝC
ЎҫҪвОцЎҝ өЪТ»ІҪ,Ј¬ұҫо}ҝјІй»щөA(chЁі)‘Ә(yЁ©ng)УГо}Ј¬ ҝЙУГлuНГН¬»\ЛјПлҪво},ЎЈ
өЪ¶юІҪ,Ј¬УЙо}ТвҝЙөГЈ¬«@„ЩөДҲцҙОәНК§”ЎөДҲцҙОҝӮ№ІУР20Јӯ3ЈҪ17Ҳц,Ј¬өГ·Цһй61Јӯ2×3ЈҪ55·Ц,ЎЈ ұҫо}ҝҙЛЖУРИэӮҖЦчуwЈ¬ҢҚ„tТтһйҪoіцЖҪҲц”ө(shЁҙ),Ј¬ТтҙЛЦ»КЈ„ЩҲцәНШ“ҲцғЙӮҖІ»Н¬өДҢҰПу,Ј¬јҙ„ЩҲцәНШ“Ҳц·Ц„eКЗ“лu”Еc“НГ”ЎЈ¶ш„ЩҲцәНШ“ ҲцөДҲцҙО”ө(shЁҙ)әНҝЙ«@өГ·e·Ц„tКЗЯ@ғЙӮҖҢҰПу№ІН¬“нУРөДМШРФ,Ј¬·Ц„eһйлuНГН¬»\Ҷ–о}ЦРөД“о^”әН“НИ”,ЎЈУЙҙЛјЩФO(shЁЁ)17 ҲцИ«КЗ„ЩҲцЈ¬ЗуіцҙЛ•r·e·Цһй5×17 =85 ,Ј¬ ұИҢҚлH¶аөГБЛ85-55ЈҪ30·Ц ,ЎЈ¶шЯ@ӮҖ30 ·ЦөДІоҫаКЗУЙШ“ҲцөГөҪЈ¬ТтҙЛУГ30 өД·e·ЦІоіэТФҶОҙО„ЩШ“ҲцөД·e·ЦІо6,Ј¬өГөҪШ“Ҳц”ө(shЁҙ)Бҝһй5,Ј¬ФЩУГҝӮҲц”ө(shЁҙ)17-5 өГөҪ„ЩҲц”ө(shЁҙ)һй12 ЎЈ јҙРЎЭxөД„ЩВКһй12÷20ЈҪ60%,ЎЈ
ТтҙЛ,Ј¬Яx“сCЯxн—ЎЈ
ЎҫХжо} 2 Ўҝ РЎГчШ“Шҹ(zЁҰ)ҢўДіЮr(nЁ®ng)ҲцөДлuө°Я\ЛНөҪРЎЩuІҝ,ЎЈ°ҙХХТҺ(guЁ©)¶Ё,Ј¬ГҝЛНөҪ1Г¶НкХыҹo“pөДлuө°Ј¬ҝЙөГЯ\ЩM0.1ФӘ,Ј»Ифлuө°УР“p,Ј¬І»ғHөГІ»өҪФ“лuө°өДЯ\ЩMЈ¬ГҝЖЖ“pТ»Г¶лuө°ЯҖТӘЩrғ”0.4ФӘЎЈРЎГч10ФВ·Э№ІЯ\ЛНлuө°25000Г¶,Ј¬«@өГЯ\ЩM2480ФӘ,ЎЈДЗФЪЯ\ЛНөДЯ^іМЦР,Ј¬лuө°ЖЖ“pБЛ ЈЁ Ј©
A.20Г¶ B.30Г¶
C.40Г¶ D.50Г¶
ЎҫҪвОцЎҝ өЪТ»ІҪ,Ј¬ұҫо}ҝјІй»щөA(chЁі)‘Ә(yЁ©ng)УГо}Ј¬ ҝЙУГлuНГН¬»\ЛјПлҪво},ЎЈ
өЪ¶юІҪ,Ј¬УЙо}ТвҝЙөГЈ¬ұҫо}·ЦһйәГлuө°әНүДлuө°ғЙӮҖҢҰПу,Ј¬ јҙлuНГН¬»\Ҷ–о}ЦРөД“лu“Еc”НГ” ¶шЯ@ғЙӮҖҢҰПуУЦУРӮҖ”ө(shЁҙ)әНЯ\ЩMғЙӮҖІ»Н¬өДМШРФ ,Ј¬јҙлuНГН¬»\Ҷ–о}ЦРөД“о^”Еc“НИ”ЎЈПИјЩФO(shЁЁ)2 5000 Г¶лuө°¶јКЗәГлuө°,Ј¬ДЗ№І‘Ә(yЁ©ng)өГөҪЯ\ЩM25000 × 0.4 = 2500 ФӘ,Ј¬ЕcҢҚлHөДЯ\ЩM2 480ФӘІоҫа2500-2480 = 20 ФӘЎЈЯ@20 ФӘөДІоҫаУЙүДлuө°әНәГлuө°өДІоҫаөГөҪ,ЎЈГҝӮҖүДлuө°ЕcәГлuө°өДЯ\ЩMІоҫаһй0 .4- ЈЁ- 0.1 Ј©= 0.5 ФӘ,Ј¬ТтҙЛүДлuө°”ө(shЁҙ)Бҝһй Г¶ЎЈ
ТтҙЛ,Ј¬Яx“сCЯxн—,ЎЈ
Ўҫ РЎҪY(jiЁҰ) Ўҝ
ёщ“ю(jЁҙ)Я@ғЙөАо}ДҝОТӮғ°l(fЁЎ)¬F(xiЁӨn)Ј¬ҢҰУЪғЙӮҖЦчуw№ІН¬“нУРғЙӮҖМШРФөДо}Дҝ,Ј¬ОТӮғҝЙТФАыУГлuНГН¬»\өДЛјПл,Ј¬НЁЯ^јЩФO(shЁЁ)·ЁЈ¬І»ФO(shЁЁ)ОҙЦӘ”ө(shЁҙ)БР·ҪіМҝмЛЩҪвҙрҶ–о},ЎЈ¶шҪвҙрөДкP(guЁЎn)жIФЪУЪ,Ј¬ңКҙ_…^(qЁұ)·ЦІДБПЦРөДІ»Н¬ЦчуwЕcМШРФЈ¬ҙ_¶ЁҝЙТФІЙУГлuНГН¬»\өДЛјПлҪвӣQҶ–о},ЎЈ
Ўҫ ЛјҫSҢ§(dЁЈo)ҲD Ўҝ

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ