2021-11-12 13:09:03 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒн(lЁўi)ФҙЈәәюұұ·ЦФә
ОДХВҒн(lЁўi)ФҙЈәәюұұ·ЦФә

Ҳу(bЁӨo)ҝјҶ–о}Ҫв»у,Јҝ
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

өИІо”ө(shЁҙ)БРКЗРРңy(cЁЁ)ЦРПІҡgҝјІмөДЦӘЧR(shЁӘ)ьc(diЁЈn),Ј¬ОТӮғёЯЦР•r(shЁӘ)әт?qЁұ)WЯ^(guЁ°)Ј¬өИІо”ө(shЁҙ)БРКЗЦёҸДөЪ¶юн—(xiЁӨng)Жр,Ј¬ГҝТ»н—(xiЁӨng)ЕcЛьөДЗ°Т»н—(xiЁӨng)өДІоөИУЪН¬Т»ӮҖ(gЁЁ)іЈ”ө(shЁҙ)өДТ»·N”ө(shЁҙ)БР,Ј¬Из1Ј¬3,Ј¬5,Ј¬7Ј¬9ҫНКЗТ»ӮҖ(gЁЁ)өИІо”ө(shЁҙ)БРөДЗ°Оен—(xiЁӨng),ЎЈКЧн—(xiЁӨng)УӣЧчa1,Ј¬Гҝн—(xiЁӨng)Ц®йgөДІоҫаУӣһ鹫ІоdЈ¬„tөЪnн—(xiЁӨng)Ң‘Ччan,Ј¬an= a1+(n-1)×d,ЎЈЗ°Гжnн—(xiЁӨng)өДәНҢ‘ЧчSnЈ¬.png) ,Ј¬НЁіЈЗйӣrПВ,Ј¬өИІо”ө(shЁҙ)БРҝјІмҢҰ(duЁ¬)НЁн—(xiЁӨng)№«КҪәНЗ°nн—(xiЁӨng)әН№«КҪөД‘Ә(yЁ©ng)УГЎЈОТӮғҒн(lЁўi)НЁЯ^(guЁ°)ҺЧөААэо}Ғн(lЁўi)ҢW(xuЁҰ)Б•(xЁӘ)өИІо”ө(shЁҙ)БР,ЎЈ
,Ј¬НЁіЈЗйӣrПВ,Ј¬өИІо”ө(shЁҙ)БРҝјІмҢҰ(duЁ¬)НЁн—(xiЁӨng)№«КҪәНЗ°nн—(xiЁӨng)әН№«КҪөД‘Ә(yЁ©ng)УГЎЈОТӮғҒн(lЁўi)НЁЯ^(guЁ°)ҺЧөААэо}Ғн(lЁўi)ҢW(xuЁҰ)Б•(xЁӘ)өИІо”ө(shЁҙ)БР,ЎЈ
ЎҫХжо}1ЎҝДілAМЭ•ю(huЁ¬)ЧhКТУР16ЕЕЧщО»,Ј¬әуТ»ЕЕұИЗ°Т»ЕЕ¶а2ӮҖ(gЁЁ)Ј¬ЧоәуТ»ЕЕУР40ӮҖ(gЁЁ)ЧщО»,ЎЈЯ@ӮҖ(gЁЁ)лAМЭ•ю(huЁ¬)ЧhКТ№ІУР()ӮҖ(gЁЁ)ЧщО»?
A.300 B.350
C.400 D.440
Ўҫҙр°ёЎҝC
ЎҫҪвОцЎҝөЪТ»ІҪ,Ј¬ұҫо}ҝјІй”ө(shЁҙ)БРҶ–о}ЎЈөЪ¶юІҪЈ¬өЪ16ЕЕУР40ӮҖ(gЁЁ)ЧщО»ЗТәуТ»ЕЕҫщұИЗ°Т»ЕЕ¶а2ӮҖ(gЁЁ)ЧщО»,Ј¬ёщ“ю(jЁҙ)НЁн—(xiЁӨng)№«КҪЈәan= a1+(n-1)×d,Ј¬ҝЙөГөЪТ»ЕЕУР40-(16-1)×2=10(ӮҖ(gЁЁ))ЧщО»Ј¬ёщ“ю(jЁҙ)ЗуәН№«КҪЈә.png) ,Ј¬ДЗГҙЯ@ӮҖ(gЁЁ)лAМЭҪМКТ№ІУРЧщО»(10+40)×16÷2=400(ӮҖ(gЁЁ)),ЎЈ
,Ј¬ДЗГҙЯ@ӮҖ(gЁЁ)лAМЭҪМКТ№ІУРЧщО»(10+40)×16÷2=400(ӮҖ(gЁЁ)),ЎЈ
ТтҙЛЈ¬Яx“сCЯxн—(xiЁӨng),ЎЈ
ЎҫХжо}2ЎҝДі№ӨҸSҢҰ(duЁ¬)13Гы№ӨИЛЯM(jЁ¬n)РРјјДЬФu(pЁӘng)ұИ,Ј¬13Гы№ӨИЛөДіЙҝғ(jЁ©)ЗЎәГіЙөИІо”ө(shЁҙ)БРЈ¬ЛщУРИЛөДЖҪҫщіЙҝғ(jЁ©)?yЁӯu)?7·Ц,Ј¬әу7ГыөДіЙҝғ(jЁ©)Ц®әНһй567·Ц,Ј¬„tөЪ1ГыөДіЙҝғ(jЁ©)КЗ()·ЦЎЈ
A.100 B.99
C.98 D.97
Ўҫҙр°ёЎҝB
ЎҫҪвОцЎҝөЪТ»ІҪ,Ј¬ұҫо}ҝјІй”ө(shЁҙ)БРҶ–о},ЎЈ
өЪ¶юІҪЈ¬УЙөИІо”ө(shЁҙ)БР№«КҪЈәөИІо”ө(shЁҙ)БРәН=(КЧн—(xiЁӨng)+Д©н—(xiЁӨng))×н—(xiЁӨng)”ө(shЁҙ)÷2=ЖҪҫщ”ө(shЁҙ)×н—(xiЁӨng)”ө(shЁҙ)=ЦРО»”ө(shЁҙ)×н—(xiЁӨng)”ө(shЁҙ),Ј¬УЙЛщУРИЛөДЖҪҫщіЙҝғ(jЁ©)?yЁӯu)?7·ЦҝЙөГөЪ7ГыөДіЙҝғ(jЁ©)?yЁӯu)?7·Ц,Ј¬әу7ГыөДіЙҝғ(jЁ©)Ц®әНһй567·ЦЈ¬ЖдЦРөДөЪТ»н—(xiЁӨng)јҙКЗөЪ7ГыіЙҝғ(jЁ©)87·Ц,Ј¬ҝЙөГөЪ13ГыөДіЙҝғ(jЁ©)?yЁӯu)?567×2÷7)-87=75(·Ц),Ј¬„tөЪ1Гыһй87+(87-75)=99(·Ц)ЎЈ
ТтҙЛ,Ј¬Яx“сBЯxн—(xiЁӨng),ЎЈ
ЎҫХжо}3ЎҝРЎАоТ»јТ3ИЛЯM(jЁ¬n)РР“Ңјt°ьУО‘тЈ¬ГҝИЛ°l(fЁЎ)1ӮҖ(gЁЁ)јt°ь,ЎЈҪY(jiЁҰ)№ыГҝИЛ“ҢөГҪро~ҝӮо~Т»ЦВ,Ј¬ҫщһй100ФӘЈ¬„ӮЗЙ3ИЛЛщ°l(fЁЎ)јt°ьҪро~һй»ҘІ»ПаН¬Хы”ө(shЁҙ)ЗТіЙөИІо”ө(shЁҙ)БР,ЎЈҶ–3ИЛЦРЛщ°l(fЁЎ)јt°ьҪро~Чо¶аөДҝЙДЬКЗ( )ФӘ?
A.197 B.198
C.199 D.200
Ўҫҙр°ёЎҝC
ЎҫҪвОцЎҝ
Ҫв·ЁТ»ЈәөЪТ»ІҪ,Ј¬ұҫо}ҝјІй”ө(shЁҙ)БРҶ–о}ЎЈ
өЪ¶юІҪ,Ј¬ГҝИЛ“ҢөҪөДјt°ьҪро~һй100ФӘҝЙЦӘИэИЛЛщ°l(fЁЎ)јt°ьҝӮҪро~һй300ФӘ,Ј¬ЗТҪро~өЪ¶ю¶аөДјt°ьјҙЖҪҫщ”ө(shЁҙ)100ФӘЎЈДЗГҙПлТӘЧоҙуөДјt°ьГжо~Чо¶а,Ј¬РиТӘЧоРЎөДјt°ьГжо~ЧоРЎ,Ј¬ЧоРЎһй1ФӘЈ¬ДЗГҙЧоҙуһй300-100-1=199(ФӘ),ЎЈ
ТтҙЛ,Ј¬Яx“сCЯxн—(xiЁӨng),ЎЈ
Ҫв·Ё¶юЈәөЪТ»ІҪЈ¬ұҫо}ҝјІй”ө(shЁҙ)БРҶ–о},Ј¬УГҙъИлЕЕіэ·ЁЗуҪв,ЎЈ
өЪ¶юІҪЈ¬о}ДҝҶ–Чоҙу,Ј¬ғһ(yЁӯu)ПИҙъИл200ФӘ,ЎЈУЙөИІо”ө(shЁҙ)БРРФЩ|(zhЁ¬)ҝЙЦӘҪро~өЪ¶ю¶аөДјt°ьјҙЖҪҫщ”ө(shЁҙ)100ФӘЈ¬јЩИзЧоҙујt°ьКЗ200ФӘ,Ј¬„t№«Іоһй100ФӘ,Ј¬ЧоРЎөДјt°ьКЗ0ФӘЈ¬ҹo(wЁІ)·Ё°l(fЁЎ)іцјt°ь;јЩИзЧоҙујt°ьКЗ199ФӘ,Ј¬„t№«Іоһй99ФӘ,Ј¬ЧоРЎөДјt°ьКЗ1ФӘЈ¬·ыәПо}Тв,ЎЈ
ТтҙЛ,Ј¬Яx“сCЯxн—(xiЁӨng)ЎЈ
ЎҫРЎҪY(jiЁҰ)Ўҝ
Я@ИэөАҶ–о},Ј¬өЪТ»о}КЗУГНЁн—(xiЁӨng)№«КҪәНЗуәН№«КҪЗуҪвЈ¬ҙујТФЪЧцо}өД•r(shЁӘ)әтөЪТ»·ҙ‘Ә(yЁ©ng)ТІ•ю(huЁ¬)КЗУГ№«КҪҪвӣQҶ–о},ЎЈөЪ¶юо}КЗПлёжФVҙујТ,Ј¬әЬ¶а•r(shЁӘ)әтЗЙУГЗ°nн—(xiЁӨng)әН=ЖҪҫщ”ө(shЁҙ)×н—(xiЁӨng)”ө(shЁҙ)=ЦРО»”ө(shЁҙ)×н—(xiЁӨng)”ө(shЁҙ)Ј¬ҝЙТФҝмЛЩҪвӣQо}Дҝ,ЎЈ¶шЧоәуТ»о}МбРСОТӮғ,Ј¬ФЪУцөҪҸН(fЁҙ)лsҶ–о}өД•r(shЁӘ)әтЈ¬ҝЙТФБРіц—lјюәуҙъИлЕЕіэЗуҪв,Ј¬јУҝмҪво}ЛЩ¶И,ЎЈ

ЎҫЛјҫSҢ§(dЁЈo)ҲDЎҝ
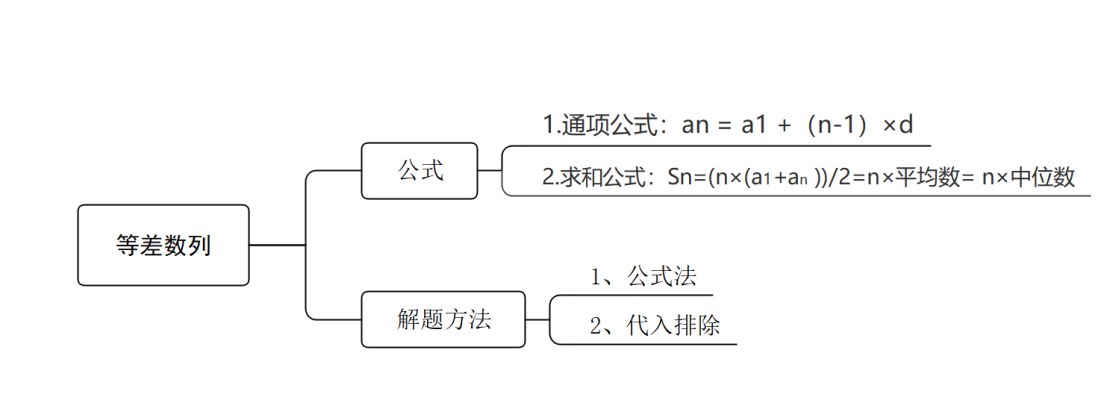

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

Ҳу(bЁӨo)Гы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc(diЁЈn)“фЛщРиЩYБПЈ¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲу(bЁӨo)ГыИлҝЪңК(zhЁіn)ҝјЧCҙтУЎҝјФҮ•r(shЁӘ)йgіЙҝғ(jЁ©)ІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ
Ҳу(bЁӨo)ҝјБчіМҲу(bЁӨo)ҝјҶ–ҙрҲу(bЁӨo)ҝј—lјюВҡДЬҪйҪBХюІЯ·ЁТҺ(guЁ©)Ҳу(bЁӨo)ҝј”ө(shЁҙ)“ю(jЁҙ)·ЦОцҡvДкҝјЗй
”ө(shЁҙ)БҝкP(guЁЎn)ПөСФХZ(yЁі)АнҪвЕР”аНЖАнЩYБП·ЦОціЈЧR(shЁӘ)ЕР”аРРңy(cЁЁ)јјЗЙ