2021-05-26 14:40:38 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁșÈ(nšši)ĂÉčĆ·ÖÔș
ÎÄŐÂíÔŽŁșÈ(nšši)ĂÉčĆ·ÖÔș

ó(bš€o)żŒî}œâ»ó,Łż
ÍŹW(xušŠ)ߎaŚÉÔ

ÔÚĐĐyżŒÔÖĐ,ŁŹÏë±Ű?cšąi)?shšŽ)ÁżêP(gušĄn)Ï”ÄŁKÊÇŽó¶à”(shšŽ)żŒÉú”ÄÀ§ëyüc(dišŁn),ŁŹ¶űÔÚ”(shšŽ)ÁżêP(gušĄn)Ï”ÄŁKÖĐ,ŁŹĆĆÁĐœMșÏÖȘŚR(shšȘ)üc(dišŁn)ÓÖÊDZ»č«ŐJ(rššn)éëyÖĐÖźëy,ŁŹœńÌìŸÍëSÖűĐĄŸÒ»ÆđíżĐÏÂß@KÓČčÇî^°ÉĄŁĐĐyżŒÔÖĐ”ÄĆĆÁĐœMșÏÖȘŚR(shšȘ)üc(dišŁn),ŁŹÖśÒȘ°üșŹÉČż·Ö,ŁŹÒ»é»ù”A(chšł)ĆĆÁĐœMșÏ;¶țéÌŰÊâĆĆÁĐœMșÏŁŹß@ÉČż·ÖłÊßfßM(jšŹn)êP(gušĄn)Ï”,ŁŹŚÎÒÍšß^Éč(jišŠ)Őn,ŁŹœÒé_ÆäÉńĂŰ”ÄĂæŒĄŁœńÌìÎÒÒ»ÆđíW(xušŠ)Á(xšȘ)һϔÚÒ»Čż·Ö,ĄŁ
»ù”A(chšł)ĆĆÁĐœMșÏ,ĄŁÆäÖĐ°üșŹÉüc(dišŁn)ŁŹŒÓ·šÔÀí,ĄąłË·šÔÀíĆcĆĆÁĐ,ĄąœMșÏ,ĄŁ
ŒÓ·šÔÀíŁșÈôÍêłÉÒ»ŒțÊÂŁŹżÉÒÔžùț(jšŽ)Äł(gšš)lŒț·Ö錷NÇér,ŁŹžś·NÇér¶ŒÄÜȘ(dšČ)ÁąÍêłÉÈÎŐ(wšŽ),ŁŹtą¶à·NÇérÓ(jšŹ)Ëăłö”ÄœY(jišŠ)čûÏàŒÓŁŹËù”Ă”ÄșÍéÍêłÉß@ŒțÊ”ķNî”(shšŽ),ĄŁłË·šÔÀíŁșÈôÍêłÉÒ»ŒțÊÂ,ŁŹĐèÒȘ?jišŁng)·ÖłÉ¶à(gšš)ČœóEÒÀŽÎÍêłÉŁŹĂż(gšš)ČœóEÈ(nšši)”ÄÈÎŐ(wšŽ)Öźég]ÓĐœ»Čæ,ŁŹtąĂż(gšš)ČœóEÓ(jšŹ)Ëăłö”ÄœY(jišŠ)čûÏàłË,ŁŹËù”ÔķeéÍêłÉß@ŒțÊ”ķNî”(shšŽ)ĄŁß@ŸÍÊÇÉŐß”Ä ^(qš±)e,ŁŹ¶űÉŽóÔÀíț(hušŹ)ŰŽ©ĆĆÁĐœMșÏÈ«ÆȘ,ŁŹÒòŽËëyüc(dišŁn)ÒČÊÇÒȘ·ÖÇćłțÊČĂŽr(shšȘ)șòÓĂŒÓ·š·ÖÊČĂŽr(shšȘ)șòœY(jišŠ)șÏłË·š·ÖČœ,ĄŁĆe(gšš)ÀęŚÓżŽÒ»ÏÂŁș
ĄŸÀę1ĄżÄłÊĐÄÊĐșÍŻč«@”œÊĐżÆŒŒđ^ÓĐ6·NȻ͏·Ÿ,ŁŹÄÊĐżÆŒŒđ^”œÊĐÉÙÄêmÓĐ5·NȻ͏·ŸŁŹÄÊĐșÍŻč«@”œÊĐÉÙÄêmÓĐ4·NȻ͏·Ÿ,ŁŹtÄÊĐșÍŻč«@”œÊĐÉÙÄêm”Ä·ŸčČÓĐŁș
A.24·N B.36·N
C.34·N D.38·N
ĄŸŽđ°žĄżC
ĄŸœâî}ˌ·ĄżÊŚÏÈ,ŁŹžùț(jšŽ)î}ÖĐÄÊĐșÍŻč«@”œÊĐÉÙÄêm”Ä·ŸÓĐŚ·NŁŹżÉĆĐàéÖ»șŹŒÓ·šÔÀíșͳ˷šÔÀí”Ä»ù”A(chšł)ĆĆÁĐœMșÏî},ĄŁ
ÆäŽÎ,ŁŹ·ÖîÓŐŁŹÈçDËùÊŸŁș
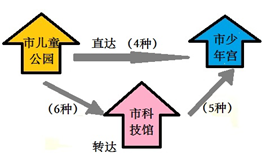
ÄÊĐșÍŻč«@”œÊĐÉÙÄêmÓĐÖ±ß_(dšą)șÍȚD(zhušŁn)ß_(dšą)Éʜ,ŁŹ·ÖîÖźégÓĂŒÓ·š;ÔÚȚD(zhušŁn)ß_(dšą)·œÊœÖĐ,ŁŹÄÊĐșÍŻč«@”œÊĐÉÙÄêm±»·ÖłÉÉČœŁŹÒȘÏÈÄÊĐșÍŻč«@”œÊĐżÆŒŒđ^,ŁŹÓĐ6·NȻ͏·Ÿ,ŁŹÔÙÄÊĐżÆŒŒđ^”œÊĐÉÙÄêmÓĐ5·NȻ͏·ŸŁŹ·ÖČœÖźégłË·š,ŁŹtżÂ·ŸčČÓĐ4+6×5=34(·N),ĄŁÒòŽËŁŹßxńCßxí(xiš€ng),ĄŁ
ĆĆÁĐœMșÏŁșĆĆÁĐ,ŁŹÄm(gšš)Ȼ͏ÔȘËŰÖĐÈÎÈĄn(gšš)ŁŹĆĆłÉÒ»ÁĐ;œMșÏ,ŁŹÄm(gšš)Ȼ͏ÔȘËŰÖĐÈÎÈĄn(gšš),ŁŹČąłÉÒ»œMŁŹÉŐß”Ä
^(qš±)eÔÚÓÚÊÇ·ńžúíĐòÓĐêP(gušĄn)Ï”,ŁŹÇ°ŐßĆcíĐòÓĐêP(gušĄn),ŁŹșóŐßĆcíĐòoêP(gušĄn),ĄŁÓ(jšŹ)Ëăr(shšȘ)ŁŹĆĆÁĐŁș ![]() =5×4,ŁŹ A =5×4×3,ŁŹ A ŁŹ=6×5×4;œMșÏŁșÒ»Æđ
^(qš±)·ÖÉ(gšš)ÀęŚÓ°É!
=5×4,ŁŹ A =5×4×3,ŁŹ A ŁŹ=6×5×4;œMșÏŁșÒ»Æđ
^(qš±)·ÖÉ(gšš)ÀęŚÓ°É!
ĄŸÀę2ĄżÉÏșŁ”œÄÏŸ©čČÓĐ43(gšš)ÜŐŸ,ŁŹèF·ŸÖéŽËĐèÒȘÊ(zhšłn)äÜƱ”Ä·N”(shšŽ)ÊÇŁș
A.43 B.1200
C.1806 D.1849
ĄŸŽđ°žĄżC
ĄŸœâî}ˌ·ĄżÊŚÏÈ,ŁŹÒÔÊŒ°l(fšĄ)ŐŸ”œœKüc(dišŁn)ŐŸéÀ꣏ÄÉÏșŁ”œÄÏŸ©ĆcÄÄÏŸ©”œÉÏșŁ,ŁŹèF·ŸÖĐèÒȘÊ(zhšłn)äÉ·NȻ͏”ÄƱ,ŁŹÉ(gšš)”Űüc(dišŁn)ÖźégĐèÒȘíĐòŁŹéĆĆÁĐî},ĄŁ
ÆäŽÎ,ŁŹÄ43(gšš)ÜŐŸÖĐÈÎßx2(gšš)ÜŐŸíÔO(shšš)ÖĂÜƱŁŹ±»ßxłöí”Ä2(gšš)ÜŐŸÓĐÏÈșóíĐò,ŁŹÓĂA±íÊŸ,ŁŹŒŽÜƱ”Ä·N”(shšŽ)ÊÇ ![]() =43×42=1806(·N)ĄŁÒòŽË,ŁŹßxńCßxí(xiš€ng)ĄŁ
=43×42=1806(·N)ĄŁÒòŽË,ŁŹßxńCßxí(xiš€ng)ĄŁ
ĄŸÀę3ĄżÄŒŚ”Ű”œÒÒ”Ű”ÄÄłŽÎÁĐÜ,ŁŹÖĐÍŸÍŁ10(gšš)ŐŸ,ŁŹtÓĐ( )·NȻ͏ÊÛr(jiš€)ĄŁ
A.55 B.66
C.110 D.132
ĄŸŽđ°žĄżB
ĄŸœâî}ˌ·ĄżÊŚÏÈ,ŁŹÒÔÊŒ°l(fšĄ)ŐŸ”œœKüc(dišŁn)ŐŸéÀę,ŁŹÄŒŚ”Ű”œÒÒ”ŰĆcÄÒÒ”Ű”œŒŚ”ŰŁŹÂ·łÌÏàÍŹ,ŁŹÒòŽËÊÛr(jiš€)ÒČÏàÍŹ,ŁŹÉ(gšš)”Űüc(dišŁn)ÖźégČ»ĐèÒȘíĐòŁŹéœMșÏî},ĄŁ![]() ÆäŽÎ,ŁŹŒŚĄąÒÒÉ”Ű,ŁŹÒÔŒ°ÖĐÍŸ10(gšš)ŐŸ,ŁŹÈ«łÌčČÓĐ12(gšš)ÜŐŸŁŹÄÖĐÈÎßx2ŐŸŒŽźa(chšŁn)ÉúÒ»·NÊÛr(jiš€)”ÄÜƱ,ŁŹŒŽčČÓĐ =66(·N)ÊÛr(jiš€),ĄŁÒòŽËŁŹßxńBßxí(xiš€ng),ĄŁ
ÆäŽÎ,ŁŹŒŚĄąÒÒÉ”Ű,ŁŹÒÔŒ°ÖĐÍŸ10(gšš)ŐŸ,ŁŹÈ«łÌčČÓĐ12(gšš)ÜŐŸŁŹÄÖĐÈÎßx2ŐŸŒŽźa(chšŁn)ÉúÒ»·NÊÛr(jiš€)”ÄÜƱ,ŁŹŒŽčČÓĐ =66(·N)ÊÛr(jiš€),ĄŁÒòŽËŁŹßxńBßxí(xiš€ng),ĄŁ
ÔőĂŽÓ,ŁŹÄăW(xušŠ)ț(hušŹ)ÁËĂŽ?ß@ŸÍÊÇĐĐyżŒÔÖДĻù”A(chšł)ĆĆÁĐœMșÏČż·Ö,ŁŹŚÎÒÒÔÒ»(gšš)ËŒŸS§(dšŁo)DÒ»ÆđżœY(jišŠ)һϻù”A(chšł)ĆĆÁĐœMșÏČż·ÖŁŹÏÂŽÎÒ»ÆđíW(xušŠ)Á(xšȘ)ÌŰÊâĆĆÁĐœMșÏ°É!
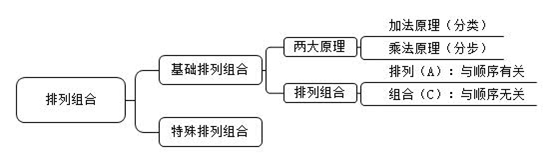

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏ,ŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉżČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ