2022-02-07 10:49:22 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒн(lЁўi)ФҙЈәФЖДП·ЦФә
ОДХВҒн(lЁўi)ФҙЈәФЖДП·ЦФә

Ҳу(bЁӨo)ҝјҶ–(wЁЁn)о}Ҫв»у,Јҝ
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

ҪьҺЧДкҝјФҮ®”(dЁЎng)ЦР,Ј¬ҺЧәОо}ҝјөДФҪҒн(lЁўi)ФҪ¶а,Ј¬ДЬүтКмҫҡҝмЛЩөДҪвҙрҺЧәОҶ–(wЁЁn)о},Ј¬КЗОТӮғұШнҡҫЯӮдөДҝјФҮДЬБҰ,Ј¬¶шҝмЛЩөДҪвҙрҺЧәОҶ–(wЁЁn)о}І»ғHРиТӘОТӮғКмПӨҺЧәОУӢ(jЁ¬)Л㹫КҪЈ¬ТІРиТӘХЖОХТ»Р©�,ЈҝјөДҺЧәОДЈР�,ЎЈФЪҺЧәОҶ–(wЁЁn)о}®”(dЁЎng)ЦРУРТ»·Nо}РНҪРЧц“Чо¶МВ·ҸҪҶ–(wЁЁn)о}”Ј¬Я@оҗо}УРЦш№М¶ЁөДҪво}МЧВ·,Ј¬ҪсМм,Ј¬ИAҲDҪМУэҫНһйҙујТФ”јҡ(xЁ¬)ЦvҪвЯ@оҗо}Ф“ИзәОЯM(jЁ¬n)РРҪвҙр!
ЎҫФӯАнТэИлЎҝУРТ»О»ҢўЬҠтTЦшсRҸДAьc(diЁЈn)өДЬҠ I(yЁӘng)іц°l(fЁЎ)·ө»ШәУҢҰ(duЁ¬)°¶өДBьc(diЁЈn)өДјТЦРЈ¬НҫЦРТӘҪӣ(jЁ©ng)Я^(guЁ°)әУMN,Ј¬ЧҢсRИҘәУАпәИЛ®,Ј¬Ф“ИзәОЯx“сВ·ҫҖЈ¬ЧҢҢўЬҠ»ШјТөДВ·іМЧо¶М?
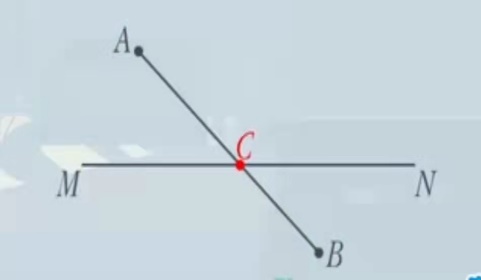
ЛјҝјЈәИзҲD,Ј¬ҢўЬҠТӘҸДAьc(diЁЈn)Ҫӣ(jЁ©ng)әУMNИҘөҪBьc(diЁЈn),Ј¬ТӘК№В·ҸҪЧо¶МЈ¬ЖдҢҚ(shЁӘ)ҫНКЗЗуABЦ®йgөДЧо¶Мҫалx,Ј¬ОТӮғ¶јЦӘөА,Ј¬ғЙьc(diЁЈn)Ц®йgҫҖ¶ОЧо¶МЈ¬ЛщТФ,Ј¬ЦұҪУЯBҪУABҪ»MNУЪCьc(diЁЈn),Ј¬„tCьc(diЁЈn)ҫНКЗҢўЬҠпӢсRөДЧојСО»ЦГЎЈ
ДЗ¬F(xiЁӨn)ФЪ,Ј¬ОТӮғҢўо}ДҝёДТ»ПВ,Ј¬Чғ?yЁӯu)йЈ?/strong>
УРТ»О»ҢўЬҠтTЦшсRҸДAьc(diЁЈn)өДЬҠ I(yЁӘng)іц°l(fЁЎ)Ј¬ПИөҪәУMNЯ…ЧҢсRәИЧгЛ®,Ј¬ФЩ·ө»ШәУ°¶Н¬ӮИ(cЁЁ)өДBьc(diЁЈn)јТЦР,Ј¬Ф“ИзәОЯx“сВ·ҫҖЈ¬ЧҢҢўЬҠ»ШјТөДВ·ҫҖЧо¶М?
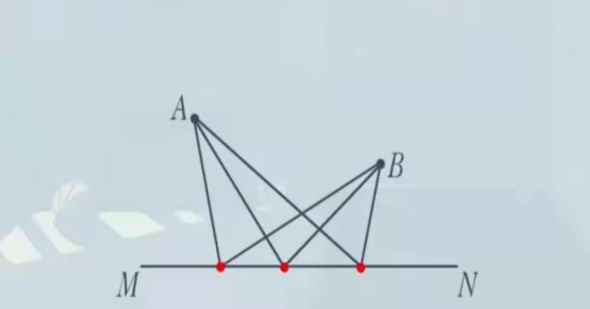
ЕcЙПТ»о}ВФһйІ»Н¬өДКЗ,Ј¬Я@•r(shЁӘ)ЬҠ I(yЁӘng)әНјТ¶јФЪәУБчөДН¬ӮИ(cЁЁ),Ј¬ДЗГҙДД·NВ·ҸҪКЗЧо¶МөДДШ?ФЪЯ@АпЈ¬ОТӮғҝЙТФАыУГЭSҢҰ(duЁ¬)·QөДЦӘЧR(shЁӘ)Ғн(lЁўi)ЯM(jЁ¬n)РРҪвҙр!
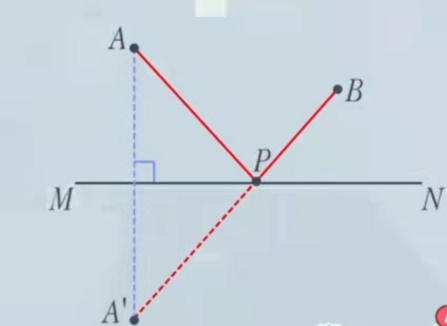

ЎҫАэо}ЎҝAьc(diЁЈn),ЎўBьc(diЁЈn)ЕcүҰөДО»ЦГИзУТҲDЛщКҫ,Ј¬¬F(xiЁӨn)ҸДAьc(diЁЈn)іц°l(fЁЎ)ТФ5ГЧ/ГлөДЛЩ¶ИЕЬПтүҰ,Ј¬ҪУУ|өҪүҰәуФЩЕЬөҪBьc(diЁЈn)Ј¬Ҷ–(wЁЁn)ЧоЙЩТӘ¶аЙЩГлөҪЯ_(dЁў)Bьc(diЁЈn)?
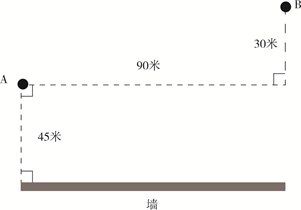
A.30
B.34
C.38
D.42
Ўҫҙр°ёЎҝA
ЎҫҪвОцЎҝҸДAьc(diЁЈn)ЕЬПтүҰГжФЩЕЬПтB,Ј¬Ҷ–(wЁЁn)ЧоЙЩРиТӘ¶аЙЩГл,Ј¬ЛЩ¶ИКЗІ»ЧғөДЈ¬ЛщТФҫНТӘЧҢВ·ҸҪұMҝЙДЬөД¶М,Ј¬ёщ“ю(jЁҙ)З°ГжөДАнХ“ЦӘЧR(shЁӘ),Ј¬ЧцПВҲDЈ¬ИзҲDЛщКҫЈә
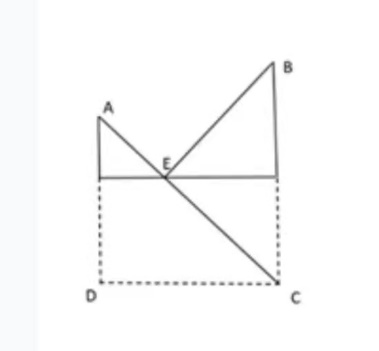

Чоәу,Ј¬ОТӮғҒн(lЁўi)ҝӮҪY(jiЁҰ)Т»ПВЗуЧо¶МВ·ҸҪөДҪво}·Ҫ·ЁЈә
Из№ыAьc(diЁЈn),ЎўBьc(diЁЈn)ФЪЦұҫҖMNөДғЙӮИ(cЁЁ)Ј¬ЗуAьc(diЁЈn)Ҫӣ(jЁ©ng)Я^(guЁ°)MNөҪЯ_(dЁў)Bьc(diЁЈn)өДЧо¶МВ·ҸҪҫНЦұҪУЯBҪУA,ЎўBғЙьc(diЁЈn)йgөДҫҖ¶ОјҙһйЧо¶МВ·ҸҪ;Из№ыAьc(diЁЈn),ЎўBьc(diЁЈn)ФЪЦұҫҖMNөДН¬ӮИ(cЁЁ)Ј¬„tТФMNһйҢҰ(duЁ¬)·QЭSЧцAьc(diЁЈn)»тBьc(diЁЈn)өДҢҰ(duЁ¬)·Qьc(diЁЈn),Ј¬ЯBҪУҢҰ(duЁ¬)·Qьc(diЁЈn)әНБнТ»ьc(diЁЈn)Ц®йgөДҫҖ¶ОјҙһйЧо¶МВ·ҸҪ,ЎЈ
ЎҫЛјҫSҢ§(dЁЈo)ҲDЎҝ
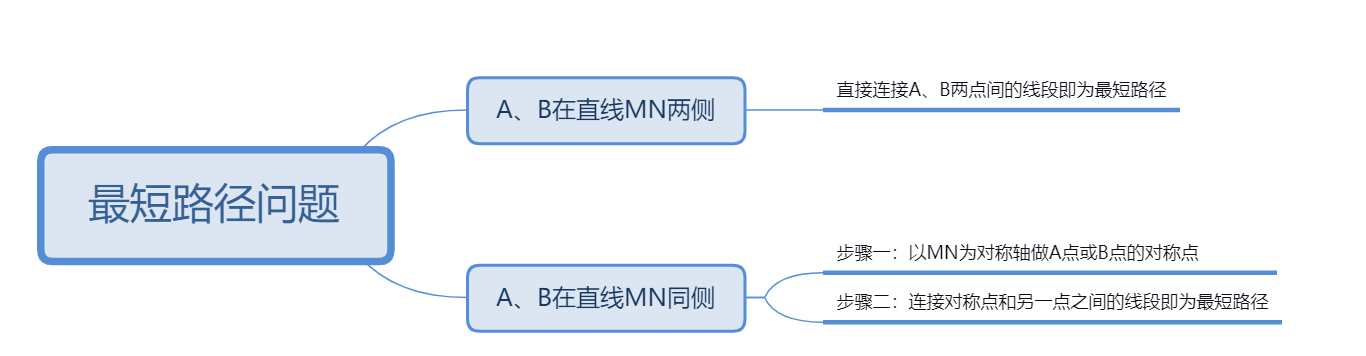

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

Ҳу(bЁӨo)Гы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc(diЁЈn)“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲу(bЁӨo)ГыИлҝЪңК(zhЁіn)ҝјЧCҙтУЎҝјФҮ•r(shЁӘ)йgіЙҝғ(jЁ©)ІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ
Ҳу(bЁӨo)ҝјБчіМҲу(bЁӨo)ҝјҶ–(wЁЁn)ҙрҲу(bЁӨo)ҝј—lјюВҡДЬҪйҪBХюІЯ·ЁТҺ(guЁ©)Ҳу(bЁӨo)ҝј”ө(shЁҙ)“ю(jЁҙ)·ЦОцҡvДкҝјЗй
”ө(shЁҙ)БҝкP(guЁЎn)ПөСФХZ(yЁі)АнҪвЕР”аНЖАнЩYБП·ЦОціЈЧR(shЁӘ)ЕР”аРРңy(cЁЁ)јјЗЙ