2022-01-12 09:55:19 Ļꥒ(w®ī)ÜTŅľ‘áĺW(w®£ng) 
 őń’¬ĀŪ(l®Ęi)‘ī£ļļĢĪĪ∑÷‘ļ
őń’¬ĀŪ(l®Ęi)‘ī£ļļĢĪĪ∑÷‘ļ

ąů(b®§o)ŅľÜĖ(w®®n)Ó}Ĺ‚Ľů,£Ņ
Õ¨ĆW(xu®¶)íŖīa◊…‘É

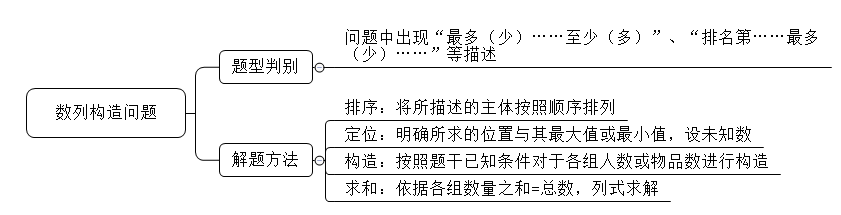
Šėƶ(du®¨)Ŗ@–©”–ĻŐ∂®Ő◊¬∑ĶńÓ},£¨ő“āÉ÷Ľ–Ť“™’∆ő’ļ√ƶ(du®¨)Ď™(y®©ng)Ķń∑Ĺ∑®,£¨”ŲĶĹƶ(du®¨)Ď™(y®©ng)ĶńÓ}ńŅ,£¨÷ĪĹ”Ő◊”√ĺÕŅ…“‘Ńň,£¨ņż»Á£ļ»›≥‚ÜĖ(w®®n)Ó},°ĘĻ§≥ŐÜĖ(w®®n)Ó}£¨◊Ó≤ĽņŻėč(g®įu)‘žÜĖ(w®®n)Ó}“‘ľįĒĶ(sh®ī)Ń–ėč(g®įu)‘žÜĖ(w®®n)Ó},°£Ō¬√śĺÕĹťĹB“ĽŌ¬ÍP(gu®°n)”ŕĒĶ(sh®ī)Ń–ėč(g®įu)‘žÜĖ(w®®n)Ó}ĶńĻŐ∂®Ĺ‚Ó}∑Ĺ∑®,°£
“Ľ°ĘÓ}–ÕŐōŁc(di®£n)£ļÓ}ł… «“™«ůĆĘ»ňĒĶ(sh®ī)ĽÚőÔ∆∑įī’’“Ľ∂®‘≠ĄtŖM(j®¨n)––∑÷ĹMĽÚ∑÷Ňš,£¨ÜĖ(w®®n)Ó}÷–≥Ų¨F(xi®§n)“◊Ó∂ŗ(…Ŕ)……÷Ń…Ŕ(∂ŗ)”,°Ę“ŇŇ√ŻĶŕ……◊Ó∂ŗ(…Ŕ)……”Ķ»√Ť Ų°£
∂Ģ,°ĘĹ‚Ó}∑Ĺ∑®£ļŇŇ–Ú-∂®őĽ-ėč(g®įu)‘ž-«ůļÕ
ŇŇ–Ú£ļĆĘňý√Ť ŲĶń÷ųůwįī’’Ūė–ÚŇŇŃ–,£¨ī_∂®◊Óīů÷ĶŇc◊Ó–°÷ĶĶńőĽ÷√°£
∂®őĽ£ļ√ųī_ňý«ůĶńőĽ÷√,£¨‘O(sh®®)őī÷™ĒĶ(sh®ī),°£
ėč(g®įu)‘ž£ļįī’’Ó}ł…“—÷™ólľĢƶ(du®¨)”ŕłųĹM»ňĒĶ(sh®ī)ĽÚőÔ∆∑ĒĶ(sh®ī)ŖM(j®¨n)––ėč(g®įu)‘ž°£
«ůļÕ£ļ“ņďĢ(j®ī)łųĹMĒĶ(sh®ī)ŃŅ÷ģļÕ=ŅāĒĶ(sh®ī),£¨Ń– Ĺ«ůĹ‚,°£
∑Ĺ∑®Ŗ\(y®īn)”√£ļ
°ĺ ĺņż°ŅőŚőĽĆW(xu®¶)…ķÖĘľ”ń≥īőŅľ‘áļů∆Ĺĺý∑÷ěť90∑÷£¨√ŅāÄ(g®®)»ňĶń∑÷∂ľěť’ŻĒĶ(sh®ī)«“ĺý≤ĽŌŗÕ¨,£¨ÜĖ(w®®n)Ķ√∑÷◊ÓĶÕĶńĆW(xu®¶)…ķ◊Ó∂ŗĶ√∂ŗ…Ŕ∑÷?
ŇŇ–Ú£ļĆĘőŚőĽÕ¨ĆW(xu®¶)įī’’∑÷?j®ęn)?sh®ī)ŹńłŖĶĹĶÕŇŇ–Ú,°£
| Ķŕ“Ľ√Ż | Ķŕ∂Ģ√Ż | Ķ໿√Ż | Ķŕňń√Ż | ĶŕőŚ√Ż |
∂®őĽ£ļÓ}ńŅÜĖ(w®®n)Ķń «Ķń∑÷◊ÓĶÕĶń£¨‘O(sh®®)ĶŕőŚ√ŻĶ√∑÷ěťx,°£
ėč(g®įu)‘ž£ļ“™ ĻĶŕőŚ√ŻĶ√∑÷◊Ó∂ŗ,£¨Ņā∑÷?j®ęn)?sh®ī)ěť90×5=450 «ĻŐ∂®÷Ķ£¨Ąt∆šňŻ»ň–Ť“™ĪMŅ…ń‹Ķń…Ŕ,£¨Ķŕňń√Ż◊Ó…Ŕěťx+1,£¨Ķ໿√Żx+2£¨“‘īňÓźÕ∆,°£
| Ķŕ“Ľ√Ż | Ķŕ∂Ģ√Ż | Ķ໿√Ż | Ķŕňń√Ż | ĶŕőŚ√Ż |
| x+4 | x+3 | x+2 | x+1 | x |
«ůļÕ£ļŅā∑÷?j®ęn)?sh®ī)ěť450,£¨Ątx+4+x+3+x+2+x+1+x=450£¨Ĺ‚Ķ√x=88,£¨ľīĶ√∑÷◊ÓĶÕĶńĆW(xu®¶)…ķ◊Ó∂ŗĶ√88∑÷,°£
»ż°Ę’śÓ}ł–÷™
°ĺņż°Ņń≥Ĺ÷Ķņ∑ĢĄ’(w®ī)÷––ńĶń80√Ż¬öĻ§Õ®Ŗ^(gu®į)ŌŗĽ•Õ∂∆ĪŖx≥Ų6√ŻńÍ∂»Éě(y®≠u)–„¬öĻ§,£¨√Ņ»ň∂ľ÷ĽÕ∂“Ľ∆Ī,£¨◊ÓĹKA°ĘB,°ĘC°ĘD,°ĘE,°ĘFŖ@6»ňģĒ(d®°ng)Ŗx,°£“—÷™A∆ĪĒĶ(sh®ī)◊Ó∂ŗ£¨Ļ≤ę@Ķ√20ŹąŖx∆Ī;B,°ĘCÉ…»ňĶń∆ĪĒĶ(sh®ī)ŌŗÕ¨,£¨≤ĘŃ–Ķŕ2;D°ĘEÉ…»ň∆ĪĒĶ(sh®ī)“≤ŌŗÕ¨,£¨≤ĘŃ–Ķŕ3;Fę@Ķ√10ŹąŖx∆Ī,£¨ŇŇ‘ŕĶŕ4°£ń«√īB,°ĘCę@Ķ√ĶńŖx∆Ī◊Ó∂ŗěť()Źą,°£
A.11B.12
C.13D.14
°ĺīūįł°ŅD
°ĺĹ‚őŲ°ŅĶŕ“Ľ≤Ĺ£¨ĪĺÓ}Ņľ≤ť◊Ó÷ĶÜĖ(w®®n)Ó}÷–ĶńĒĶ(sh®ī)Ń–ėč(g®įu)‘žÜĖ(w®®n)Ó},°£
Ķŕ∂Ģ≤Ĺ,£¨łýďĢ(j®ī)«į ŲĶńĹ‚Ó}∑Ĺ∑®£¨ŇŇ–Ú-∂®őĽ-ėč(g®įu)‘ž-«ůļÕ,£¨“ņÓ}“‚Ō»ŇŇ–Ú,°Ę∂®őĽŃ–≥ŲĪŪłŮ»ÁŌ¬£ļ
| A | B | C | D | E | F |
| 20 | x | x | 10 |
“™ ĻB°ĘCŖx∆Ī◊Ó∂ŗ∆šňŻ»ň–Ť“™ĪMŅ…ń‹Ķń…Ŕ,£¨”÷D,°ĘE∆ĪĒĶ(sh®ī)ŌŗÕ¨«““™Ī»F∂ŗ£¨Ļ ,£¨D,°ĘE◊Ó…Ŕ»°11°£
Ķ໿≤Ĺ,£¨Ņā∆ĪĒĶ(sh®ī)ěť80∆Ī,£¨«ůļÕ£¨20+x+x+11+11+10=80,£¨Ĺ‚Ķ√x=14,£¨ľīD°ĘF◊Ó∂ŗĶ√14∆Ī,°£
“Úīň,£¨ŖxďŮDŖxŪó(xi®§ng)°£
Õ®Ŗ^(gu®į)«į ŲĶń ĺņżļÕ’śÓ},£¨Ōŗ–Ňīůľ“Ď™(y®©ng)‘ď’∆ő’ŃňĹ‚õQĒĶ(sh®ī)Ń–ėč(g®įu)‘žÜĖ(w®®n)Ó}Ķń∑Ĺ∑®,°£∑Ĺ∑®ĶńŽyŁc(di®£n)‘ŕ”ŕėč(g®įu)‘žĶńŖ^(gu®į)≥Ő£¨“™◊–ľö(x®¨)Ķń∑÷őŲ«Ś≥ĢÓ}ł…Ķń“™«ů,£¨»Ű«ů◊Ó∂ŗ,£¨∆šňŻĶńŃŅĺÕĪMŅ…ń‹Ķń…Ŕ;«ů◊Ó…Ŕ£¨∆šňŻŃŅĺÕ–Ť“™ĪMŅ…ń‹Ķń∂ŗ°£Ŗ@ÓźÓ}–Ť“™≥š∑÷ĹY(ji®¶)ļŌÓ}ł…Ķń“™«ůľįólľĢ,£¨Õ®Ŗ^(gu®į)ŇŇ–Ú-∂®őĽ-ėč(g®įu)‘ž-«ůļÕŖ@∑N∑Ĺ∑®«ů≥Ųƶ(du®¨)Ď™(y®©ng)Ķńīūįł,°£

ŌŗÍP(gu®°n)É»(n®®i)»›Õ∆ň]£ļ

ŔN–ńŅľĻęŅÕ∑Ģ

ŔN–ńĆ£ĆŔŅÕ∑Ģ
…Ō“Ľ∆™£ļ2022––úy(c®®)ĒĶ(sh®ī)ŃŅÍP(gu®°n)ŌĶ£ļ∆śŇľŐō–‘∑®°™Ĺoń„–¬ňľ¬∑
Ō¬“Ľ∆™£ļ2022 °Ņľ––úy(c®®)ĒĶ(sh®ī)ŔY÷ģ≤ŚŅ’∑®Ĺ‚ŇŇŃ–ĹMļŌÜĖ(w®®n)Ó}

ąů(b®§o)√ŻólľĢ?
ćŹőĽŖxďŮ?
ĻP‘áŅ∆ńŅ?
√ś‘á∑Ĺ Ĺ?
......

 ‘ŕĺÄŅÕ∑Ģ°Ń
‘ŕĺÄŅÕ∑Ģ°Ń

Łc(di®£n)ďŰňý–ŤŔYŃŌ£¨íŖīaÓI(l®ęng)»°








’–ŅľĻęłśŅľ‘áīůĺV¬öőĽĪŪąů(b®§o)√Ż»ŽŅŕú (zh®≥n)Ņľ◊CīÚ”°Ņľ‘áēr(sh®™)ťg≥…ŅÉ(j®©)≤ť‘É√ś‘á√ŻÜőšõ”√Ļę ĺŅľ‘áŅž”ć
ąů(b®§o)ŅľŃų≥Őąů(b®§o)ŅľÜĖ(w®®n)īūąů(b®§o)ŅľólľĢ¬öń‹ĹťĹB’Ģ≤Ŗ∑®“é(gu®©)ąů(b®§o)ŅľĒĶ(sh®ī)ďĢ(j®ī)∑÷őŲövńÍŅľ«ť
ĒĶ(sh®ī)ŃŅÍP(gu®°n)ŌĶ—‘’Z(y®≥)ņŪĹ‚Ň–ĒŗÕ∆ņŪŔYŃŌ∑÷őŲ≥£◊R(sh®™)Ň–Ēŗ––úy(c®®)ľľ«…