2022-01-04 13:29:36 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәФЖДП·ЦФә
ОДХВҒнФҙЈәФЖДП·ЦФә

ҲуҝјҶ–о}Ҫв»у,Јҝ
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

ёчО»ХэФЪӮдҝјөДРЎ»п°й,Ј¬ҪсМмОТӮғТ»ЖрҒнҢW(xuЁҰ)Б•(xЁӘ)Уа”ө(shЁҙ)МШРФФЪ”ө(shЁҙ)БҝкP(guЁЎn)ПөБҝҪв·ҪіМЦРөД‘Ә(yЁ©ng)УГЎЈ·ҪіМ·ЁКЗ”ө(shЁҙ)БҝкP(guЁЎn)ПөҪво}·Ҫ·ЁөДөЪТ»·Ҫ·Ё,Ј¬ДЬҺНЦъОТӮғҪвӣQәЬ¶ао}Дҝ,Ј¬ө«·ҪіМ·ЁТІУРЖдұЧ¶ЛЈ¬Ҫв·ҪіМРиТӘ»ЁЩMөД•rйgЭ^¶а,Ј¬ҪсМмОТӮғҫНТ»ЖрҒнҢW(xuЁҰ)Б•(xЁӘ)Т»ӮҖ·ЦОц·ҪіМөДјјЗЙ-Уа”ө(shЁҙ)МШРФ,Ј¬ҒнҺНЦъОТӮғёьәГөДИҘ·ЦОц·ҪіМЎЈ
КЧПИОТӮғҒнҝҙЦӘЧRьcЈәУа”ө(shЁҙ)ҫЯУРҝЙјУРФ,ЎўҝЙңpРФ,ЎўҝЙіЛРФ(іЈУГіэТФ3,Ўў9өИ”ө(shЁҙ)“ю(jЁҙ)),ЎЈ
ҝЙјУРФЈә28+16=44,44іэТФ3Уа2,Ј¬ҝЙТФІр·Цһй28іэТФ3Уа1,16іэТФ3Уа1Ј¬Уа1+Уа1=Уа2;
ҝЙңpРФЈә28-16=12,12іэТФ3Уа0,Ј¬ҝЙТФІр·Цһй28іэТФ3Уа1,16іэТФ3Уа1,Ј¬Уа1-Уа1=Уа0;
ҝЙіЛРФЈә28×16=448,448іэТФ3Уа1,Ј¬ҝЙТФІр·Цһй28іэТФ3Уа1,16іэТФ3Уа1,Ј¬Уа1×Уа1=Уа1;
ЧўЈәУа”ө(shЁҙ)КЗҝЙТФЮD(zhuЁЈn)»ҜөДЈ¬ұИИз25іэТФ3,Ј¬ЙМһй8Уа1,Ј¬ЙМһй7Уа4,Ј¬ЙМһй6Уа7,Ј¬јҙіэТФ3Уа1ЎўУа4ЎўУа7КЗөИғrөД
ҪУПВҒнОТӮғНЁЯ^ҺЧӮҖАэо}ҒнҝҙТ»ПВУа”ө(shЁҙ)МШРФөДҫЯуw‘Ә(yЁ©ng)УГЈә
ЎҫАэ1Ўҝ35246×17693=()
A.623637478 B.623627478 C.623617478 D.623607478
ҪвОцЈә35246іэТФ9Уа2,17693іэТФ9Уа8,Ј¬Уа2×Уа8=Уа16Ј¬іэТФ9Уа16өИғrУЪіэТФ9Уа7,Ј¬ТтҙЛҙр°ёЯxн—іэТФ9ұШУа7,ЎЈAЯxн—іэТФ9Уа1Ј¬ЕЕіэ,Ј¬BЯxн—іэТФ9Уа0,Ј¬ЕЕіэЈ¬CЯxн—іэТФ9Уа8,Ј¬ЕЕіэ,Ј¬DЯxн—іэТФ9Уа7Ј¬Хэҙ_,Ј¬ТтҙЛЯx“сDЯxн—,ЎЈ
ЎҫАэ2ЎҝДіЧгЗтұИЩҗКЫіц40ФӘЎў80ФӘ,Ўў120ФӘйTЖұ№І2000ҸҲ,Ј¬ЖдЦР80ФӘөДйTЖұ”ө(shЁҙ)КЗ120ФӘөДйTЖұ”ө(shЁҙ)өД2ұ¶Ј¬ұИЩҗйTЖұКХИл№І12ИfФӘ,ЎЈ„t40ФӘйTЖұКЫіц¶аЙЩҸҲ?
A.1000
B.1150
C.1200
D.1250
ҪвОцЈәұҫо}ҝјІй»щөA(chЁі)‘Ә(yЁ©ng)УГо},Ј¬ФO(shЁЁ)40ФӘөДйTЖұУРxҸҲЈ¬120ФӘөДйTЖұУРyҸҲ,Ј¬„t80ФӘөДйTЖұУР2yҸҲ,Ј¬ёщ“ю(jЁҙ)ҝӮ”ө(shЁҙ)һй2000ҸҲҝЙТФБРіцөИКҪЈ¬x+3y=2000,Ј¬3yіэТФ3Уа0,2000іэТФ3Уа2,Ј¬ёщ“ю(jЁҙ)Уа”ө(shЁҙ)өДҝЙјУРФҝЙ·ЦОціцxіэТФ3Уа2Ј¬јҙУа2+Уа0=Уа2,Ј¬AіэТФ3Уа1,Ј¬ЕЕіэ;BіэТФ3Уа1Ј¬ЕЕіэ;CіэТФ3Уа0ЕЕіэ;DіэТФ3Уа2,Ј¬Хэҙ_,Ј¬ТтҙЛЯx“сDЯxн—,ЎЈ
ЎҫАэ3ЎҝДіҙОМпҸҪЯ\„У•юЦРЈ¬ЯxКЦ…ўјУёчҶОн—ұИЩҗУӢИлЛщФЪҲF(tuЁўn)уwҝӮ·ЦөДТҺ(guЁ©)„tһйЈәТ»өИӘ„өГ9·Ц,Ј¬¶юөИӘ„өГ5·Ц,Ј¬ИэөИӘ„өГ2·ЦЎЈјЧк №ІУР10О»ЯxКЦ…ўЩҗ,Ј¬ҫщ«@Ә„�,Ј¬F(xiЁӨn)ЦӘјЧк ЧоәуҝӮ·Цһй61·ЦЈ¬Ҷ–Ф“к Чо¶аУРҺЧО»ЯxКЦ«@өГТ»өИӘ„?
A.3
B.4
C.5
D.6
ҪвОцЈәұҫо}ҝјІйІ»¶Ё·ҪіМҶ–о},Ј¬ФO(shЁЁ)«@өГТ»өИӘ„өДУРxО»ЯxКЦ,Ўў«@өГ¶юөИӘ„өДУРyО»ЯxКЦЎў«@өГИэөИӘ„өДУРzО»ЯxКЦ,ЎЈёщ“ю(jЁҙ)№І10О»ЯxКЦ…ўЩҗәНҝӮ·Цһй61·Ц,Ј¬ҝЙБРІ»¶Ё·ҪіМҪMЈәx+y+z=10ўЩЈ¬9x+5y+2z=61ўЪ,Ј¬ўЪ-ўЩ×2ҝЙөГЈә7x-3y=41,ЎЈНЁЯ^Уа”ө(shЁҙ)МШРФ·ЦОцЈ¬41іэТФ3Уа2,3yіэТФ3Уа0,Ј¬„t7xіэТФ3Уа2,Ј¬УЦТтһй7іэТФ3Уа1,Ј¬ТтҙЛxіэТФ3Уа2,Ј¬Ц»УРCЯxн—қMЧгЈ¬Яx“сCЯxн—,ЎЈ
ЧоәуҢўҪсМмЦӘЧRьcҪoҙујТХыАнһйЛјҫSҢ§(dЁЈo)ҲDЈә
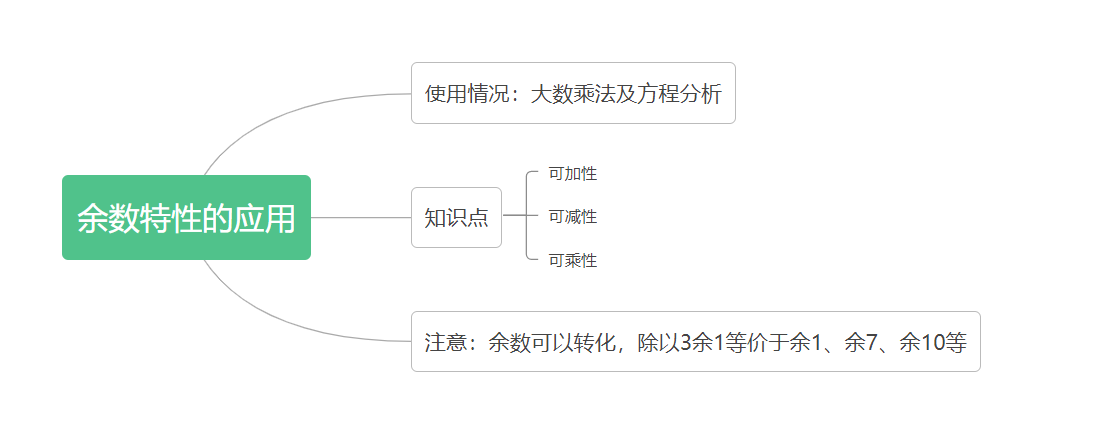

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю
ЙПТ»ЖӘЈә2022ДкәюДПКЎҝјРРңy”ө(shЁҙ)БҝкP(guЁЎn)ПөӮдҝјЦ®ПааҸЕcІ»ПааҸҶ–о}
ПВТ»ЖӘЈә2022КЎҝјРРңyӮдҝј”ө(shЁҙ)БҝкP(guЁЎn)ПөЦ®ұ¶”ө(shЁҙ)МШРФ

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБПЈ¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңК(zhЁіn)ҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ