2022-01-04 13:09:22 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁșșțÄÏ·ÖÔș
ÎÄŐÂíÔŽŁșșțÄÏ·ÖÔș

ó(bš€o)żŒî}œâ»ó,Łż
ÍŹW(xušŠ)ߎaŚÉÔ

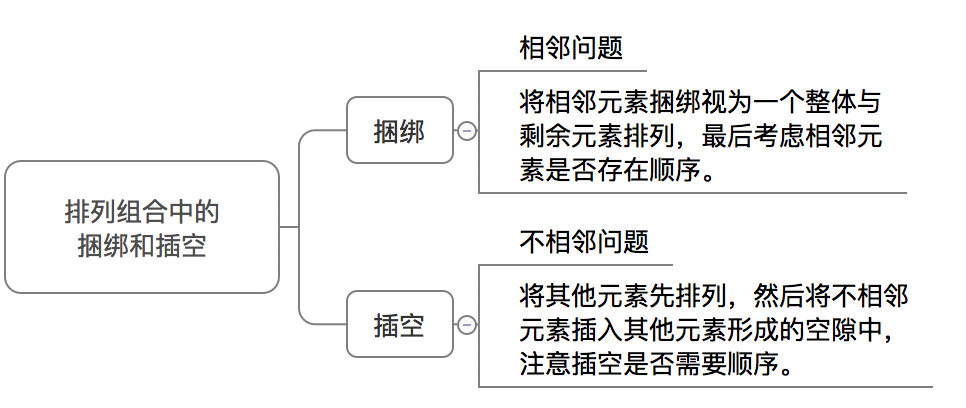
șțÄÏÊĄżŒĐĐy”(shšŽ)ÁżêP(gušĄn)Ï”ÖĐ”ÄĆĆÁĐœMșÏÊÇĂżÄê±ŰżŒ”Äî}ĐÍŁŹĆĆÁĐœMșÏÖĐÓĐŚ(gšš)ÌŰÊâÄŁĐÍŁŹ°üÀšÀŠœ,ĄąČćżŐ,Ąąžô°ćĄąće(cuš°)λĆĆÁĐ,Ąąh(hušąn)ĐÎĆĆÁĐ”È,ŁŹœńÌìĐĄŸÏÈœoŽóŒÒœéœBÒ»ÏÂÀŠœșÍČćżŐĄŁ
êP(gušĄn)ÓÚÀŠœșÍČćżŐȘ(yš©ng)ÓĂ”Äî}ĐÍŒ°Śö·šÒϱíŁș
| îĐÍ | Ș(yš©ng)ÓĂî}ĐÍ | Śö·š |
| ÀŠœ | Ïààî} | ąÏààÔȘËŰÀŠœÒéÒ»(gšš)ŐûówĆcÊŁÓàÔȘËŰĆĆÁĐ,ŁŹŚîșóżŒ]ÏààÔȘËŰÊÇ·ńŽæÔÚíĐò,ĄŁ |
| ČćżŐ | Č»Ïààî} | ąÆäËûÔȘËŰÏÈĆĆÁĐŁŹÈ»șóąČ»ÏààÔȘËŰČćÈëÆäËûÔȘËŰĐγɔĿŐ϶ÖĐ,ŁŹŚąÒâČćżŐÊÇ·ńĐèÒȘíĐò,ĄŁ |
ÒęÀę1ŁșAĄąB,ĄąC,ĄąDĄąEÎćÈËŐŸłÉÒ»ĆĆ,ŁŹÆäÖĐA,ĄąBÉÈ˱ŰíŐŸÒ»ÆđŁŹÇóÓжàÉÙ·NŐŸ·š?
·ÖÎöŁșA,ĄąBÉÈ˱ŰíŐŸÒ»Æđ,ŁŹŐfĂśAĄąBÉÈËÒȘÏàà,ŁŹÏàà”Äî}ÓĂÀŠœ·š,ĄŁ
”ÚÒ»ČœŁŹÎÒÏÈąA,ĄąBÉÈËÀŠœÔÚÒ»Æ𿎳ÉÒ»(gšš)ÈË,ŁŹÈ»șóĆcCĄąD,ĄąEÈę(gšš)ÈËßM(jšŹn)ĐĐÈ«ĆĆÁĐÇér”(shšŽ)é;
”Ú¶țČœ,ŁŹżŒ]AĄąBÉÈËÈ(nšši)Čż”ÄÈ«ĆĆÁĐíĐòÇér”(shšŽ)é;
”ÚÈęČœ,ŁŹżŐŸ·šÓĐ×=24×2=48,ĄŁ
œÓÏÂíÎÒíżŽÒ»”ÀŐæî}ĄŁ
ĄŸÀę1ĄżÄłöżÆŒŒŐŻÓĐ5G,ĄąÈËč€ÖÇÄÜ,Ąą ^(qš±)KæĄąŽó”(shšŽ)ț(jšŽ)șÍÔÆÓ(jšŹ)Ëă5(gšš)Öśî},ŁŹĂż(gšš)Öśî}ÓĐ2λ°l(fšĄ)ŃÔŒÎÙe,ĄŁÈçčûÒȘÇóĂż(gšš)Öśî}”ÄŒÎÙe°l(fšĄ)ŃÔŽÎĐò±ŰíÏàà,ŁŹčČÓжàÉÙ·NȻ͏”Ä°l(fšĄ)ŃÔŽÎĐò?
A.120
B.240
C.1200
D.3840
·ÖÎöŁșÒȘÇóĂż(gšš)Öśî}2λŒÎÙe°l(fšĄ)ŃÔŽÎĐò±ŰíÏààŁŹÏààî}ÓĂÀŠœ,ĄŁ
”ÚÒ»Čœ,ŁŹ·Öeą5(gšš)Öśî}”ÄĂż2λŒÎÙeÀŠœÔÚÒ»Æ𿎳ÉÒ»(gšš)ÈËŁŹÏÈœo5(gšš)ÀŠœßM(jšŹn)ĐĐĆĆĐòÇér”(shšŽ)é=120;
”Ú¶țČœ,ŁŹ5(gšš)ÀŠœÈ(nšši)Ăż2(gšš)È˶ŒÓĐ=2”ÄÈ(nšši)ČżÈ«ĆĆÁĐíĐò;
”ÚÈęČœ,ŁŹŚîœK”Ä°l(fšĄ)ŃÔÇér”(shšŽ)é×()5=120×32>120×30=3600ĄŁ
ÒòŽË,ŁŹßxńDßxí(xiš€ng),ĄŁ
ŽóŒÒW(xušŠ)ț(hušŹ)ÓĂÀŠœ·šœâQÏààî}ÁËá?ÏÂĂæÎÒíżŽČ»Ïààî}ĄŁ
ÒęÀę2ŁșA,ĄąB,ĄąCĄąD,ĄąEÎćÈËŐŸłÉÒ»ĆĆ,ŁŹÆäÖĐAĄąBÉÈËČ»ÄÜŐŸÒ»Æđ,ŁŹÇóÓжàÉÙ·NŐŸ·š?
·ÖÎöŁșA,ĄąBÉÈËČ»ÄÜŐŸÒ»ÆđŁŹŒŽA,ĄąBČ»Ïàà,ŁŹČ»Ïàà”Äî}ÓĂČćżŐĄŁ
”ÚÒ»Čœ,ŁŹÏÈĆĆC,ĄąDĄąEÈęÈË,ŁŹÇér”(shšŽ)é;
”Ú¶țČœ,ŁŹCĄąD,ĄąEÈęÈËźa(chšŁn)Éú4(gšš)żŐ,ŁŹÄ4(gšš)żŐßxłö2(gšš)żŐąAĄąB·Öe·ĆßM(jšŹn)È„,ŁŹÇér”(shšŽ)é(A,ĄąBÉÈËȻ͏ŁŹČćżŐr(shšȘ)ÓĐíĐò);
”ÚÈęČœ,ŁŹżÇér”(shšŽ)é×=6×12=72ĄŁ
ÏÂĂæÎÒíżŽÒ»”ÀŐæî},ĄŁ
ĄŸÀę2ĄżÒòë·žÄÔì,ŁŹëÁŠč«ËŸÓ(jšŹ)ÎŽíÊźÌìŠ(dušŹ)ijХ ^(qš±)ßxńÈęÌìÍŁë,ŁŹÒȘÇóČ»ÄÜßBÀm(xšŽ)ÉÌìͣ룏tčČÓжàÉÙ·NÍŁë·œ°ž?
A.35
B.56
C.84
D.120
·ÖÎöŁșî}ÄżÒȘÇóČ»ÄÜßBÀm(xšŽ)ÉÌìÍŁë,ŁŹŒŽÒȘÇóÍŁëČ»Ïàà,ŁŹČ»Ïàà”Äî}ÓĂČćżŐĄŁ
”ÚÒ»Čœ,ŁŹČ»ÍŁë”Ä7Ììźa(chšŁn)Éú8(gšš)żŐ;
”Ú¶țČœ,ŁŹÄ8(gšš)żŐßx3(gšš)żŐŁŹÓĐÇér”(shšŽ)=56(ÍŁë”Ä3ÌìÏàÍŹ,ŁŹČ»żŒ]íĐò),ĄŁ
ÒòŽËŁŹßxńBßxí(xiš€ng),ĄŁ
êP(gušĄn)ÓÚÀŠœșÍČćżŐŽóŒÒW(xušŠ)ț(hušŹ)ÁËá,ŁŹÚsŸoŐÒĐ©î}ÄżŸÁ(xšȘ)Æđí°ÉĄŁ

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț
ÉÏÒ»ÆȘŁș2022œÌKÊĄżŒ”(shšŽ)ÁżêP(gušĄn)Ï”ÙYÁÏ·ÖÎöäżŒÓ(jšŹ)
ÏÂÒ»ÆȘŁș2022űżŒĐĐyäżŒŁș”(shšŽ)ÁżêP(gušĄn)Ï”œâ·œłÌÖźÓà”(shšŽ)ÌŰĐÔ

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏ,ŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉżČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒŽđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé