�Мy(c��)����,����շ������нM�ϼ����ʆ��}
2021-07-01 09:19:08����(w��)�T��ԇ�W(w��ng) ����(l��i)Դ���A�D����
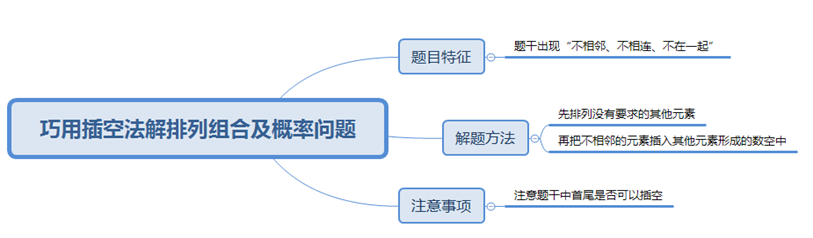
��Ԓ�f(shu��)“�Ô�(sh��)���ߵ��Мy(c��)”,����(sh��)���P(gu��n)ϵ���҂��Мy(c��)�Ă俼�����P(gu��n)��Ҫ,���������нM�ϼ������ǔ�(sh��)���P(gu��n)ϵ��һ��(g��)���^�y�е�Ӳ���^,��һ�㿼�鿼����(du��)���A(ch��)���нM�ϼ�����֪�R(sh��)�����ռ��䑪(y��ng)�á�

���нM�ϼ������ڽ����꿼ԇ�п��l��,��������ʽ���^�`��,�����H���������c�M�ϼ����ʻ����ĸ������߀��(hu��)����һЩ����ķ���,������������,����շ������巨���h(hu��n)������,�����в�շ���һ�N�,����ĸ��l�������ҷ�����������,�����÷�,������Ͳ�շ��}Ŀ�����c(di��n)���ض����}�����o����M(j��n)��Ԕ��(x��)�Ľ�B��
�}���R(sh��)�e��
�����нM�ϼ����ʵ��}Ŀ��,������}���г��F(xi��n)“������”,��“�����B”��“����һ��”���~�Z(y��),���t���ǿ����շ�,���䱾�|(zh��)���ǽ�Q���нM���в������Ć��}��
���}������
��շ��Ľ��}˼·��“���ź��”,�����w���}���E���£����Ȳ����]�������w,���������������w;����ٰ�Ҫ������������Ԫ�ز��뵽����Ԫ�����γɵĔ�(sh��)������,��������Ҫע������}����“��λ”�Ƿ���Բ��;���o(w��)�����f(shu��)���t������Ԫ�ؿ��Բ�������Ԫ�ص���βλ�ã���t��β�����Բ��,��
�eһ��(g��)��(ji��n)�ε������f(shu��)��һ�´��}�Ľ��}������ij�W(xu��)УA,��B��C,��D,��E��5�����(du��)���n�g�٣�����A,��B���˲�����һ��,���tһ���ж��ٷN���(du��)��ʽ?
����(j��)“A��B���˲�����һ��”��֪���}�����շ�,������������������3��C,��D��E,������![]() ���(du��)��ʽ,������ź�C��D,��E���γ�4��(g��)��(sh��)�գ���?g��u)?��(g��)��(sh��)�����x��2��(g��)���벻�����ă���A,��B,���t�ɝM��A��B���˲�����һ��,������
���(du��)��ʽ,������ź�C��D,��E���γ�4��(g��)��(sh��)�գ���?g��u)?��(g��)��(sh��)�����x��2��(g��)���벻�����ă���A,��B,���t�ɝM��A��B���˲�����һ��,������![]() (�N)���(du��)��ʽ,��һ����
(�N)���(du��)��ʽ,��һ����![]() (�N)���(du��)��ʽ,��(ֵ��ע����ǣ����}�]�������f(shu��)��,����C,��D��E��β�����Բ��,���t�γ���4��(g��)��(sh��)��,�����}Ŀ�f(shu��)��A��B���˲���������β,����ζ��C,��D��E��λ���ܲ��,���tֻ���γ�2��(g��)Ԫ���g��(sh��)��,��)
(�N)���(du��)��ʽ,��(ֵ��ע����ǣ����}�]�������f(shu��)��,����C,��D��E��β�����Բ��,���t�γ���4��(g��)��(sh��)��,�����}Ŀ�f(shu��)��A��B���˲���������β,����ζ��C,��D��E��λ���ܲ��,���tֻ���γ�2��(g��)Ԫ���g��(sh��)��,��)
����Ԏ����}��(l��i)�o���չʾ���@��}Ŀ���������}�^��,��
����1��(2015���(gu��)��)��12��ͬ�ӵ��ɘ��6��ͬ�ӵİؘ�Nֲ�ڵ�·�ɂ�(c��),��ÿ��(c��)�Nֲ9��,��Ҫ��ÿ��(c��)�İؘ䔵(sh��)������Ҳ��������ҵ�·���c(di��n)�ͽK�c(di��n)̎�ɂ�(c��)�Nֲ�Ķ�������ɘ�,�����ж��ٷN��ͬ�ķNֲ����?
A. 36
B. 50
C. 100
D. 400
���𰸡�C
�������������}��,���}ĿҪ��“ÿ��(c��)�İؘ䔵(sh��)������Ҳ�����”��ÿ��(c��)�ؘ�Ҫ����������Q���������}�҂����ò�շ�,����?y��n)��}ĿҪ��ÿ��(c��)9�Ø��Ұؘ䔵(sh��)����ͬ,��Ҳ�����f(shu��)18 �Ø�ֳɵ�·��߅�M(j��n)��ֲ�䣬ÿ��(c��)�Nֲ6�w�ɘ��c3�w�ؘ�,���}Ŀ߀Ҫ��ؘ䲻����,�����������ò�շ����Ȍ�6�w�ɘ�Nֲ��,����?y��n)��ɘ���ͬ�ӵ�,�����?img height="25" src="https://u3.huatu.com/uploads/allimg/210701/image_4.png" style="cursor: default;" width="42" />�N��ʽ;�ٌ������İؘ�����ѽ�(j��ng)�Nֲ�õ��ɘ���ȥ��6 �w�ɘ�֮�g�γ�7��(g��)��,�����}Ŀ��Ҫ���·���c(di��n)�ͽK�c(di��n)̎�ɂ�(c��)�Nֲ�Ķ�������ɘ�,������·�ɶ˲��ܲ���ؘ䣬��6�w�ɘ�֮�g�γ� 5 ��(g��)��,����![]() �N��ʽ,�� ͬ���ɵã���·��һ��(c��)Ҳ��
�N��ʽ,�� ͬ���ɵã���·��һ��(c��)Ҳ��![]() �N��ʽ,�������_�𰸞�
�N��ʽ,�������_�𰸞�![]() =100�N��ʽ,��
=100�N��ʽ,��
��ˣ��x��C�x�(xi��ng),��
����2��(2021���)�ɂ�(g��)���ˎ��Ă�(g��)����ȥ��ֻ������(g��)λ�õĈA�����D(zhu��n)ľ�R,����ô�ɂ�(g��)���˲������ĸ��ʞ飺
A.2/5
B.3/5
C.1/3
D.2/3
���𰸡�B
�������������}�ɣ� ,���M����r��(sh��)Ҫ��ɂ�(g��)���˲�����,����Q���������}�҂����ò�շ����t�����Ă�(g��)С��,���Ă�(g��)С���h(hu��n)�����з�����
,���M����r��(sh��)Ҫ��ɂ�(g��)���˲�����,����Q���������}�҂����ò�շ����t�����Ă�(g��)С��,���Ă�(g��)С���h(hu��n)�����з�����![]() �N,����?y��n)��ǭh(hu��n)�����У�4��(g��)С��ֻ���γ�4��(g��)��,���ɂ�(g��)���˲������t���ɂ�(g��)���˲�չ���
�N,����?y��n)��ǭh(hu��n)�����У�4��(g��)С��ֻ���γ�4��(g��)��,���ɂ�(g��)���˲������t���ɂ�(g��)���˲�չ���![]() �N,��������r��6�˭h(hu��n)�����У�����
�N,��������r��6�˭h(hu��n)�����У�����![]() �N,���ɂ�(g��)���˲������ĸ���=72/120=3/5,��
�N,���ɂ�(g��)���˲������ĸ���=72/120=3/5,��
��ˣ��x��B�x�(xi��ng),��
ͨ�^���ώ��������}���v��,�����Ŵ�Ҍ�(du��)���нM�ϼ�������,����շ��}Ŀ���Єe�Լ����}�^�̶�����һ�����˽⣬ϣ����ҿ������ղ�շ��}Ŀ�������Լ����}����,�������}�r(sh��)�J(r��n)���м�(x��),�����ܹ��˴���}Ŀ��ϣ�������(l��i)��ྚ��(x��),���ܱM�����ս��}����!
��˼�S��(d��o)�D��
����������
- 1 2023ɽ�|�ij��Ж|���h������I(y��)��λ�a(b��)�����M(j��n)��(y��u)������
- 2 2024���K�K������Dž^(q��)���M(j��n)��(y��u)��У�L(zh��ng)�Ǹɽ̎�16��
- 3 2023�V�|�V������ɳ�^(q��)��������Ƹ�I(y��)�̎�����
- 4 2023���հ��c��ͩ�ǎ����ߵ��,��ƌW(xu��)У��Ƹ35��
- 5 2024�����������(hu��)���(xi��ng)��Ƹ�˲Ŏ��Y92��
- 6 2023ɽ�|�I���в��d�h���wϵ�y(t��ng)��Ƹ��С�W(xu��)�̎�����
- 7 2023�V�|�V������ɳ�^(q��)������(li��n)�ϏV�Fһ�н������F(tu��n)����
�����俼��
- 1 ��Փ��������Փ�����}���h�����E
- 2 ��Փ��������Փ��ԇ�Л]���y���}��,��ֻ���y�IJ���
- 3 ��Փ�������俼֮���Č���
- 4 �Мy(c��)�������F��ʡ����(sh��)�Y�����y�ȷ���
- 5 �Мy(c��)���������ٹ����Z(y��)����գ�Ԓ�}һ�±��д���
- 6 �Мy(c��)�俼������(ch��ng)���Мy(c��)�����_���}���
- 7 ��Փ��������Փ��(f��)��(x��)��ץ�o
- 8 ��Փ����������3����x����,�������뚢��Փ����




