2022-02-08 16:34:07 ¿¨í(w´Ç)T¢¥åƒW(w´Èng) 
 öáíôÚåÇȤV|ñøå¤
öáíôÚåÇȤV|ñøå¤

µ¢¥Ÿ}§ã£µ,È¢
ë˜W(xu´Î)ÔÇaæèå

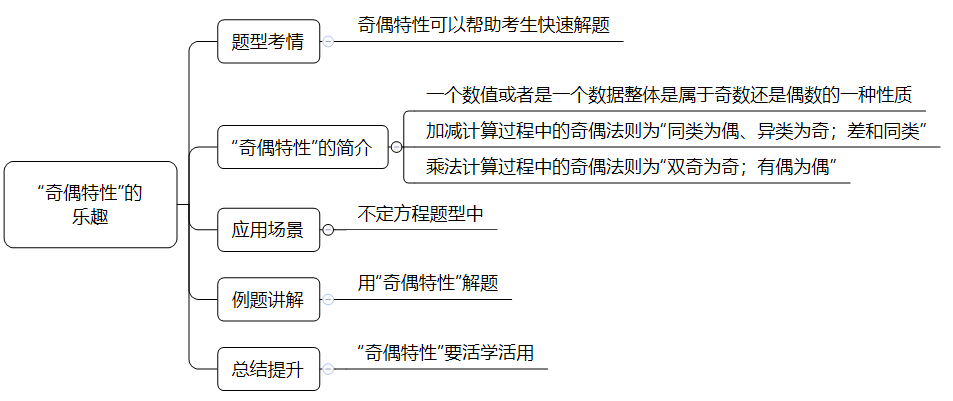
ö´¢šý£óóȘÔ@òúÅÅy¢¥åçáíÌâÚ,ȘÆàóðÎÆÖç(sh´Ç)ê¢õP(gu´Àn)üç¤ëìYêüñøö—Úíf,Ș“¢š”°èêùøóìçáøÄ؈ñ´ÀÈíf秓¢š”,Șáúƒëý£çûý£äÓóÌé¥äÄÅå”êù,ȘáúûÇ“óÌé¥äÄÅå”ç§çæòúØ£ñNå¾ûÇÆçáÅåì|(zh´˜)áÄ?§ÆüôÚȘå܃ëå¥çħo¡¼ö£¢¥èº§Õ§B¤öÕ“óÌé¥äÄÅå”,ÀÈ
1.“óÌé¥äÄÅå”çᤧÕ
ùªø^çá“óÌé¥äÄÅå”,ȘŠHèüƒëòúø¡Ø£ç(sh´Ç)ø磷íÔòúØ£ç(sh´Ç)±(j´Ç)í«µwòúìÆÖóÌç(sh´Ç)Ôòúé¥ç(sh´Ç)çáØ£ñNÅåì|(zh´˜)ÀÈåÖ§ãŸ}Ô^°äøÅ,ȘóÌé¥äÄÅåáÉ·ëøº¢¥èº¢šùìçÄéé°»Íeí`çáÔxÚ,Șáѽ¢sÅÀÔxþçáñѺÀÈ
ùátÔ\ùÐøÅý£ë˜çáÔ\ùÐ,ȘóðóÌé¥ñ´tòúý£Ø£Æ,Șأ¯Ð¢èØåwÕèǵŸÈ˜Ø£ŸÕ¥ÆpÆùÐÔ^°äøÅçáóÌé¥ñ´t,ȘأŸÕ°ù°»ÆùÐÔ^°äøÅçáóÌé¥ñ´t,ÀÈ
¥ÆpÆùÐÔ^°äøÅçáóÌé¥ñ´tՓ똟Õé¥ÀÂÛŸÕóÌ;ýŸ¤ë똟”,ȘƒÔµwàÓüôȤ
óÌç(sh´Ç)±óÌç(sh´Ç)=é¥ç(sh´Ç),Șé¥ç(sh´Ç)±é¥ç(sh´Ç)=é¥ç(sh´Ç)ÀÈ
óÌç(sh´Ç)±é¥ç(sh´Ç)=óÌç(sh´Ç),Șé¥ç(sh´Ç)±óÌç(sh´Ç)=óÌç(sh´Ç),ÀÈ
Æ^ýš¢èØå¯l(f´À)˜F(xi´Ên),ȘåÖA±B=CçáÆùÐÔ^°äøÅȘà¶A,ÀÂBçáÑ¥òúóÌç(sh´Ç)£·íÔÑ¥òúé¥ç(sh´Ç)r,Ș¥ÇAÀÂBŸeìÅåüÁë˜r,Șù«çáÆùЧY(ji´Î)¿«ƒªòúé¥ç(sh´Ç),Ș¤ñQՓ똟Õ饔;à¶AÀÂBŸeìÅåý£ë˜r,Ș¥ÇA,ÀÂBøÅØ£ÕóÌç(sh´Ç)Ø£Õé¥ç(sh´Ç)rȘù«çáÆùЧY(ji´Î)¿«ƒªòúóÌç(sh´Ç),Ș¤ñQÕ“ÛŸÕóÌ”ÀÈ
Çùëã,ȘåÖA±B=CçáÆùÐÔ^°äøÅ,Șà¶A+BçáÆùЧY(ji´Î)¿«ÕóÌç(sh´Ç),ȘtA-BçáÆùЧY(ji´Î)¿«ØýÝÄà£ÕóÌç(sh´Ç);à¶A+BçáÆùЧY(ji´Î)¿«Õé¥ç(sh´Ç),ȘtA-BçáÆùЧY(ji´Î)¿«ØýÝÄà£Õé¥ç(sh´Ç);ñÇøÛØÁà£,ÀÈA+BçáÆùЧY(ji´Î)¿«ÇºÝÚ¤ëȘA-BçáÆùЧY(ji´Î)¿«ÇºÝÚýŸ,Ștèç(sh´Ç)øÛ¤ëçáŸeìÅå¤ëÔ@èç(sh´Ç)øÛýŸçáŸeìÅåüÁë˜,ȘñÇøÛØÁà£,Ș¤ñQÕ“ýŸ¤ë똟”,ÀÈ
°ù°»ÆùÐÔ^°äøÅçáóÌé¥ñ´t,ȘØå°ùñ´Õø¼È˜°»ñ´ˆ(y´ˋng)ßD(zhu´Èn)£₤Õ°ùñ´¤µåìÔMÅÅóÌé¥ñøö—,ÀÈåÖ°ùñ´ÆùÐÔ^°äøÅȘóðóÌé¥ñ´tÕ“ŠpóÌÕóÌ;ÆÅé¥Õ饔,ȘƒÔµwàÓüôȤ
óÌç(sh´Ç)×óÌç(sh´Ç)=óÌç(sh´Ç);óÌç(sh´Ç)×é¥ç(sh´Ç)=é¥ç(sh´Ç);é¥ç(sh´Ç)×é¥ç(sh´Ç)=é¥ç(sh´Ç),ÀÈ
Æ^ýš¢èØå¯l(f´À)˜F(xi´Ên)ȘåÖA×B=CçáÆùÐÔ^°äøÅȘà¶A,ÀÂBçáÑ¥òúóÌç(sh´Ç)r,Șù«çáÆùЧY(ji´Î)¿«òúóÌç(sh´Ç),Ș¤ñQÕ“ŠpóÌÕóÌ”;à¶A,ÀÂBøÅÆÅé¥ç(sh´Ç)rȘù«çáÆùЧY(ji´Î)¿«òúé¥ç(sh´Ç),Ș¤ñQÕ“ÆÅé¥Õ饔,ÀÈ
ý£¿Éòú¥ÆpÆùÐÔ^°äøÅçáóÌé¥ñ´t,ȘÔòú°ù°»ÆùÐÔ^°äøÅçáóÌé¥ñ´t,Șù■Ñ¥ìÆÖ“óÌé¥äÄÅå”,Ș¡¼ö£¢¥èºåÖæ—Ÿ}Ô^°äøÅأѴ؈æÅ¥ ^(q´Ý)ñøåÆùÐòúìÆÖ¥ÆpȘÔòú°ù°»,Șáѽ¡ª±(j´Ç)ý£ÆûçáÔ\ùÐýèÆûΈ(y´ˋng)çáóÌé¥ñ´t,ÀÈ
2.“óÌé¥äÄÅå”çáˆ(y´ˋng)Æû—ƒ¯
“óÌé¥äÄÅå”ë´°Èòúˆ(y´ˋng)ÆûåÖý£Ñ´ñ§°äçáŸ}ÅëøÅȘطÕý£Ñ´ñ§°äí»ûÌúµ§ãòúÝàï^âÏŠyçá,Șأ¯ÐÑ¥ýèÆûà(c´´)ûÌñøö—çáñ§ñ´ÚÇ_Ñ´ÇÞ¯¡È˜Ñ½“óÌé¥äÄÅ唃ëòúÆûçáÝàï^ÑÁçáØ£ñNà(c´´)ûÌñøö—ñ§ñ´êù,ÀÈ
àÓåÖçáÔ\ùÐøÅ,ȘÂÀÂ,À¢ǰèà»ç(sh´Ç)±(j´Ç)í«µw,ȘtÔ@à»ç(sh´Ç)±(j´Ç)í«µwåÖæ—¥Æñ´Ô\ùÐ,Șà¶øˆçâêùÀÂ,ÀÂÔ@à»í«µwøÅàöØãèç(sh´Ç)±(j´Ç)í«µwçáóÌé¥ìÅå,ȘáúûǃëÝÄà£áÉ·¡ª±(j´Ç)¥ÆpÆùÐçáóÌé¥ñ´tÚëó°—çÖà»ç(sh´Ç)±(j´Ç)í«µwçáóÌé¥ìÅå;êÚëãȘÎÆÖ¤ëÔ@èí«µwøÅ,ȘA¤ëxÀÂB¤ëyåÖæ—°ùñ´Ô\ùÐ,Șt¢è¡ª±(j´Ç)°ùñ´ÆùÐçáóÌé¥ñ´tÚéÅÑ´,ÀÂÔ@èç(sh´Ç)±(j´Ç)í«µwçáóÌé¥äÄÅåÀÈ
3.⻟}øv§ã
Àƒâ»1À¢ñ§°äçá§ãÕ,ȘƒªÕì|(zh´˜)ç(sh´Ç),ȘtçáøçÕ()Ȥ
A.194B.197
C.199D.201
ÀƒÇÞ¯¡À¢A
Àƒ§ãö—À¢ÂǺàŠñ§°äȘçû,ÀÈØ·Õp,ÀÂqåÖæ—¥Æñ´È˜úØóðÆùЧY(ji´Î)¿«99ÕóÌç(sh´Ç),Șt¡ª±(j´Ç)¥ÆpÆùÐÔ^°äøÅçáóÌé¥ñ´tøÅ“ÛŸÕó̔Ș¢èøˆp,ÀÂqÝÄà£ÕÛŸ,Ș¥ÇØ£ÕóÌç(sh´Ç)Ø£Õé¥ç(sh´Ç)ÀÈŸ}á¢úµçáøç,ȘåÖæ—°ùñ´ÆùÐ,ȘúØp,ÀÂqØ£óÌØ£é¥,ȘtÆÅé¥ç(sh´Ç),Ș¡ª±(j´Ç)°ùñ´ÆùÐÔ^°äøÅçáóÌé¥ñ´tøÅ“ÆÅé¥Õ饔,ȘtçáøçÝÄÕé¥ç(sh´Ç)ÀÈÆ^ýšÔxÚȘ¢èØåéé°»BCDȘ¿òÔxAÔxÚÀÈ
ë´Ô^èüûÌçáâ»æÆȘöدl(f´À)˜F(xi´Ên)ˆ(y´ˋng)Æû“óÌé¥äÄÅå”Ç_¢èØåëøºöØ¡■¢šçħãQá°ñNŸÅëçáŸ}á¢ÀÈÛà£È˜“óÌé¥äÄÅå”Øýý£òúØ£°èý£æçáȘ¡¼ö£¢¥èºˆ(y´ˋng)åš`£Ÿˆ(y´ˋng)ÆûȘüŠØˆêù§ã¡■ÑÁçá“óÌé¥äÄÅå”çáûŸàÊȘ¡¼ö£¢¥èº¢èâ^âm(x´Ç)õP(gu´Àn)æÂàAD§äÆ»,ÀÈ

üÁõP(gu´Àn)à(n´´i)àïëóù]Ȥ

ìNÅᢥ¿¨¢ëñ±

ìNÅáÈì¢ëñ±
èüØ£óˆÈ¤2022òÀ¢¥ÅÅy£ªóÖÝàøÄÀˆ¿âùÐçá¼àêÎ
üôØ£óˆÈ¤2022òÀ¢¥ÅÅyð¢¥È¤§(j´ˋng)ºâ«øÛ§y(t´₤ng)£IŸŸ}

µû«l¥±?
ö£Ôxþ?
¿På¢óá¢?
ûÌåñ§ò§?
......

 åÖƒ¢ëñ±Àê
åÖƒ¢ëñ±Àê

■c¶ùªÅÒìYêü,ȘÔÇaŸI(l´¨ng)àÀ








íÅ¢¥¿¨¡Ì¢¥åǵƒVôö£ÝÚµû«àŠ¢Öò¢¥æCÇ·ÆÀ¢¥årÕg°è¢ýÕåûÌåû«öðÆû¿¨òƒ¢¥å¢šÆ