2022-02-07 15:32:18 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁșÉœÎś·ÖÔș
ÎÄŐÂíÔŽŁșÉœÎś·ÖÔș

óżŒî}œâ»ó,Łż
ÍŹW(xušŠ)ߎaŚÉÔ

2021ÄêÉœÎśÊĄżŒ”(shšŽ)ÁżêP(gušĄn)Ï”î}ÄżÓÉÍùÄê”Ä10”Àî}ÔöŒÓ”œÁË15”Àî}ÄżŁŹî}Áż”ÄÔöŒÓÒČï@ÊŸłöÁËÔÚč«żŒß^łÌÖĐŠ”(shšŽ)W(xušŠ)ËŒŸSżŒČé”ÄÖŰÒłÌ¶È,ŁŹœY(jišŠ)șÏœüÄêíßM(jšŹn)Ăæ·ÖÖ”ÒȘÇóÔœíÔœžß,ŁŹÈçčûżŒÔrÍêÈ«·Ć”(shšŽ)ÁżêP(gušĄn)Ï”î}ÄżŁŹŸÍșÜëyÄĂ”œÒ»žß·Ö?jš«n)?shšŽ),ŁŹÒČŸÍo·šéłÉčŠÉÏ°¶ŽòÏÂÁŒșÔĻù”A(chšł),ĄŁ¶ű”(shšŽ)ÁżêP(gušĄn)Ï”ÖźËùÒÔëyŁŹÔÒòÖźÒ»ÊÇÒòÆäî}ÄżŸCșÏĐÔ(qišąng),ŁŹŠżŒÉúßĘËŒŸSÄÜÁŠÒȘÇóĘ^žß,ŁŹ”«ÊÇ”(shšŽ)Áżëmëy,ŁŹșܶàî}Äż sÓĐÖű±ÈĘ^(qišąng)”ÄŒŒÇÉĐÔŁŹ¶űÇÒÒ»Đ©ÖȘŚRücÒČÔÚvÄê”ÄżŒÔî}Äżź(dšĄng)ÖжàŽÎłöŹF(xiš€n),ŁŹËùÒÔÈçčûÎÒżÉÒÔW(xušŠ)Á(xšȘ)ČąŐÆÎŐß@Đ©î}Äż,ŁŹŸÍÄÜÔÚ¶ÌrégÈ(nšši)Çóœâłöß@îî}ÄżĄŁÆäÖĐ,ŁŹŚîÖ”î}±ăÊÇÊĄżŒÖĐĆcÆäËûîĐÍżŒücœY(jišŠ)șÏżŒČéîlÂÊĘ^žß”ÄÒ»î,ŁŹÀęÈçŚșÎÇóŚîÖ”ŁŹœ(jš©ng)ú(jšŹ)Àûî}ÇóŚîÖ”,ŁŹ¶ŒÓĂ”œÁËÏàȘ(yš©ng)”ÄŚîÖ”ÀíŐ,ŁŹœÓÏÂíĐĄŸŸÍŠŚîÖ”î}ßM(jšŹn)ĐĐŐÊöŁŹÏŁÍûŠžśÎ»ÍŹW(xušŠ)ÓĐËùÍÖú,ĄŁ
ÀíŐÖȘŚR
1.Ò»ÔȘ¶țŽÎ·œłÌÇóŚîÖ””ÄȘ(yš©ng)ÓĂŁș![]() ,ŁŹ(1)ź(dšĄng)a>0rŁŹyÔÚ
,ŁŹ(1)ź(dšĄng)a>0rŁŹyÔÚ![]() ÌÈĄ”ĂŚîĐĄÖ”
ÌÈĄ”ĂŚîĐĄÖ”![]() ;(2)ź(dšĄng)a<0r,ŁŹyÔÚ
;(2)ź(dšĄng)a<0r,ŁŹyÔÚ![]() ÌÈĄ”ĂŚîŽóÖ”
ÌÈĄ”ĂŚîŽóÖ”![]() ,ĄŁ
,ĄŁ
2.Ÿù֔Ȼ”ÈÊœÀíŐ”ÄȘ(yš©ng)ÓĂŁșa+b≥2![]() (aĄąbŸùéŐęŐû”(shšŽ),ŁŹź(dšĄng)ÇÒHź(dšĄng)a=br”ÈÌłÉÁą),ĄŁ
(aĄąbŸùéŐęŐû”(shšŽ),ŁŹź(dšĄng)ÇÒHź(dšĄng)a=br”ÈÌłÉÁą),ĄŁ
ÒÀț(jšŽ)Ÿù֔Ȼ”ÈÊœŁŹżÉ”ĂŠÓÚÒ»ŸŰĐζűŃÔ,ŁŹ(1)ÖÜéLCÒ»¶šr,ŁŹĂæ·eSÈĄ”ĂŚîŽóÖ”ŁŹ![]() ;(2)Ăæ·eSÒ»¶šr,ŁŹÖÜéLCÈĄ”ĂŚîĐĄÖ”,ŁŹ
;(2)Ăæ·eSÒ»¶šr,ŁŹÖÜéLCÈĄ”ĂŚîĐĄÖ”,ŁŹ![]() ,ĄŁ
,ĄŁ
œâî}ˌ·ĆcŒŒÇÉ
Ó^Čìî}ÄżÔO(shšš)·œÊœ,ŁŹÇóŚîŽó»òŚîĐĄÇÒÉ挰ÉÏÊöÀíŐÖȘŚRź(dšĄng)ÖĐ”ÄÄÄÒ»,ŁŹŽ_¶šșóÌŚÓĂč«ÊœŒŽżÉ,ĄŁ
Àęî}Ÿ«Öv
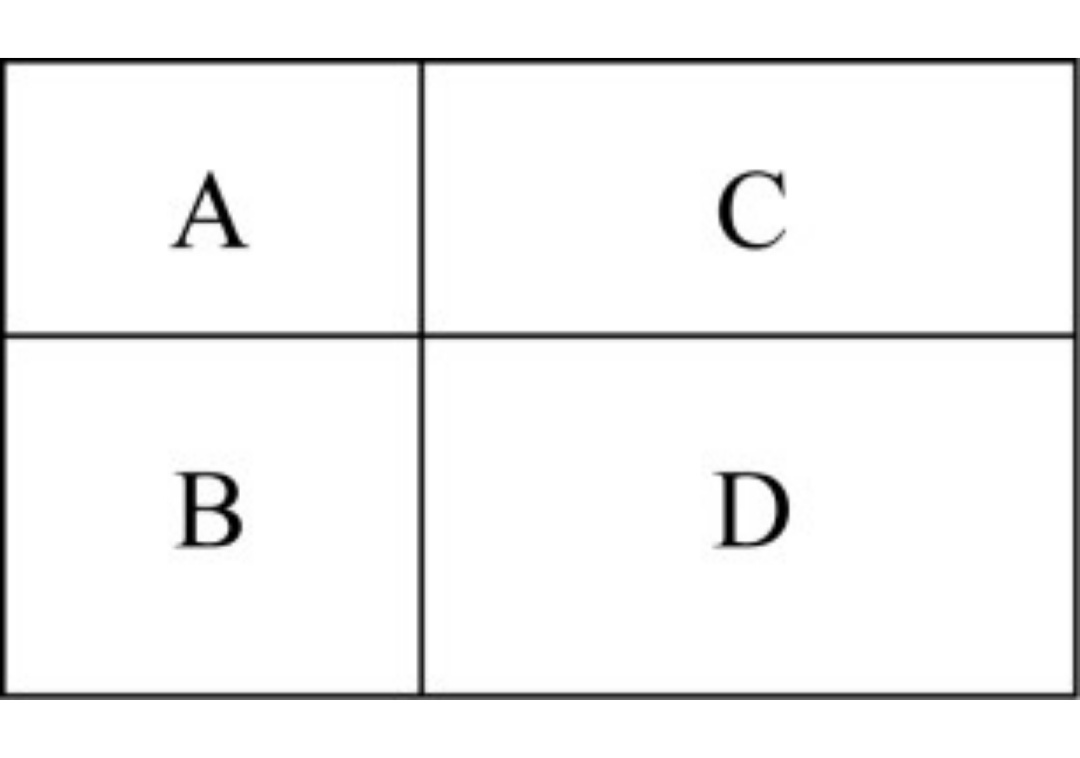
ĄŸÀę1Ąż(2020ÄêÂ(lišąn)żŒ)ŽćĂńÌŐÄłłĐ°üÒ»KéL·œĐηNÖČ”Ű,ŁŹËûą”Ű·ÖžîłÉÈçDËùÊŸ”Ä4ĐĄéL·œĐÎ,ŁŹÔÚA,ĄąB,ĄąC,ĄąDËÄKéL·œĐÎÍÁ”ŰÉÏ·Öe·NÖČÎśčÏ,Ąą»šÉúĄą”ŰčÏ,ĄąËź”Ÿ,ĄŁÆäÖĐéL·œĐÎAĄąBĄąC”ÄÖÜéL·ÖeÊÇ20ĂŚ,Ąą24ĂŚ,Ąą28ĂŚŁŹÄÇĂŽéL·œĐÎD”ÄŚîŽóĂæ·eÊÇŁș
A.42Æœ·œĂŚB.49Æœ·œĂŚ
C.64Æœ·œĂŚD.81Æœ·œĂŚ
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéŚșÎŚîÖ”î},ĄŁ
”Ú¶țČœŁŹÔO(shšš)A”ÄéL·Öeéa,Ąąb,ŁŹta+b=10ŁŹBĆcAéLÏàÍŹ,ŁŹÔO(shšš)Æäéc,ŁŹta+c=12ŁŹCĆcAÏàÍŹ,ŁŹÔO(shšš)ÆäéLéd,ŁŹtb+d=14ŁŹDĆcBÏàÍŹ,ŁŹĆcCéLÏàÍŹ,ŁŹtc+d=(a+c)+(b+d)-(a+b)=12+14-10=16ŁŹtDÖÜéLé32,ĄŁ
”ÚÈęČœŁŹÓÉŸù֔Ȼ”ÈÊœżÉ”Ă,ŁŹź(dšĄng)ÖÜéLÒ»¶šr,ŁŹĂæ·eÈĄ”ĂŚîŽóÖ”![]() ĄŁ
ĄŁ
ÒòŽË,ŁŹßxńCßxí,ĄŁ
ĄŸÀę2Ąż(2019ÄêÉîÛÚ)ÄłîÉÌÆ·°ŽÙ|(zhšŹ)Áż·Öé8nŽÎŁŹŚî”ÍnŽÎÉÌÆ·ĂżŒțżÉ«@Àû8ÔȘ,ŁŹĂżÌážßÒ»nŽÎ,ŁŹtĂżŒțÉÌÆ·”ÄÀûÔöŒÓ2ÔȘĄŁŚî”ÍnŽÎÉÌÆ·ĂżÌìżÉźa(chšŁn)łö60Œț,ŁŹĂżÌážßÒ»nŽÎ,ŁŹtÈŐźa(chšŁn)ÁżpÉÙ5ŒțĄŁÈôÖ»Éúźa(chšŁn)ÆäÖĐÄłÒ»nŽÎ”ÄÉÌÆ·,ŁŹtĂżÌìÄÜ«@”ÔČîŽóÀûÊÇ()ÔȘ,ĄŁ
A.620B.630
C.640D.650
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»ČœŁŹœ(jš©ng)ú(jšŹ)Àûî}ŚîÖ”(yšu)»Żî,ĄŁ
”Ú¶țČœ,ŁŹÔO(shšš)ÌáÉęÁËnnŽÎŁŹżÀûéy,ŁŹžùț(jšŽ)żÀû=ĂżŒțÉÌÆ·”ÄÀû×äNÊÛÁż,ŁŹżÉ”Ă![]() ,ŁŹÁîy=0ŁŹœâ”Ăn1=-4,ŁŹn2=12,ŁŹź(dšĄng)
,ŁŹÁîy=0ŁŹœâ”Ăn1=-4,ŁŹn2=12,ŁŹź(dšĄng)![]() rŁŹyÈĄ”ĂŚîŽóÖ”,ĄŁ
rŁŹyÈĄ”ĂŚîŽóÖ”,ĄŁ
”ÚÈęČœ,ŁŹyŚîŽóÖ”=(8+2×4)×(60-5×4)=640ÔȘĄŁ
ÒòŽË,ŁŹßxńCßxí,ĄŁ
žùț(jšŽ)Àęî}2żÉÒÔżŽłöÍšłŁÇérÈçčûąyÖ”łÉÉ”(shšŽ)ÏàłË”ÄĐÎÊœŁŹß@ÓČ»ĐèÒȘÔÙÓŚĄŠ·QĘSč«Êœ,ŁŹÏàŠžüÈĘÒŚÇóœâ,ŁŹč(jišŠ)ÊĄrégĄŁ
ŸCÉÏżÉÒÔżŽłö,ŁŹœ(jš©ng)ú(jšŹ)Àûî}ŚîÖ”(yšu)»ŻîÒÔŒ°ŚșÎî}ÇóŚîÖ”łŁłŁÊÇĆcșŻ”(shšŽ)î}ÏàœY(jišŠ)șÏ,ŁŹÒòŽËŁŹÖ»ÒȘŽóŒÒŐÆÎŐÁËșŻ”(shšŽ)ÇóŚîÖ””ÄÏàȘ(yš©ng)ŒŒÇÉ,ŁŹß@îî}±ăżÉÓÈжűœâ!

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț

óĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

ücôËùĐèÙYÁÏ,ŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íóĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔrégłÉżČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ