2022-01-04 10:53:26 ╣½äš(w©┤)åT┐╝įćŠW(w©Żng) 
 ╬─š┬üĒį┤Ż║║■─ŽĘųį║
╬─š┬üĒį┤Ż║║■─ŽĘųį║

ł¾(b©żo)┐╝å¢Ņ}ĮŌ╗¾,Ż┐
═¼īW(xu©”)Æ▀┤aū╔įā

Į³─Ļ,Ż¼ąą£y(c©©)┼ąöÓ═Ų└Ē─ŻēKäō(chu©żng)ą┬┐╝Ņ}Ņl│÷,Ż¼┴ŅįSČÓ┐╝╔·┤ļ╩ų▓╗╝░,Ż¼„÷╚╗╔±é¹,ĪŻė╚Ųõ╩ŪłDą╬═Ų└ĒęÄ(gu©®)┬╔ŅÉ▓┐ĘųŻ¼Ė³╩Ūīó“ŲĮ├µ┐╝³c(di©Żn)┴ó¾w╗»”Ą─└Ē─Ņ▓╗öÓĄž═ŲĻÉ│÷ą┬,Ż¼äō(chu©żng)ęŌ╩«ūŃ,ĪŻ╚ńŽ┬Ņ}Ż║
ĪŠ└²Ī┐Å─╦∙ĮoĄ─╦─éĆ(g©©)▀xĒŚ(xi©żng)ųąŻ¼▀xō±ūŅ║Ž▀mĄ─ę╗éĆ(g©©)╠Ņ╚ļå¢╠¢(h©żo)╠Ä,Ż¼╩╣ų«│╩¼F(xi©żn)ę╗Č©Ą─ęÄ(gu©®)┬╔ąįŻ║
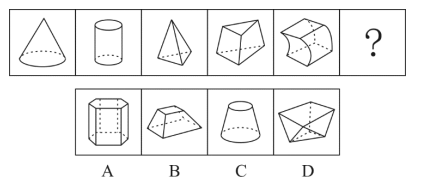
Ņ}Ė╔╝░▀xĒŚ(xi©żng)╦∙ėąłDą╬Š∙×ķ┴ó¾włD,Ż¼║▄ČÓ┐╝╔·š`ęį×ķ▒žČ©┐╝▓ķ┴ó¾wŅÉ┐╝³c(di©Żn),Ż¼ŲõīŹ(sh©¬)▓╗╚╗Ż¼┤╦Ņ}┐╝³c(di©Żn)ģs╩Ū┴ó¾włDą╬ųą├µĄ─éĆ(g©©)öĄ(sh©┤),Ż¼Ęųäe×ķ2,Īó3Īó4,Īó5,Īó6Ż¼╣╩å¢╠¢(h©żo)╠Ä┴ó¾włDą╬├µĄ─éĆ(g©©)öĄ(sh©┤)×ķ7,Ż¼D▀xĒŚ(xi©żng)×ķš²┤_┤░Ė,ĪŻęį═∙“├µ”Ą─┐╝▓ķų„ę¬¾w¼F(xi©żn)į┌ŲĮ├µÄū║╬łDą╬ųąŻ¼Č°┤╦Ņ}ģsīóŲĮ├µłDą╬┐╝³c(di©Żn)ė╔┤╦╝░▒╦,Ż¼▀\(y©┤n)ė├į┌┴╦┴ó¾włDųą,Ż¼╩«Ęųėą╚żĪŻ“ŲĮ├µ┐╝³c(di©Żn)┴ó¾w╗»”Ą─└Ē─Ņį┌▀@Ą└Ņ}ųąŪÕ╬·Ąž¾w¼F(xi©żn),ĪŻŅA(y©┤)£y(c©©)ęį║¾Ģ■(hu©¼)ėąĖ³ČÓ“ŲĮ├µ┐╝³c(di©Żn)┴ó¾w╗»”Ą─┐╝Ņ}│÷¼F(xi©żn),Ż¼Č°┐╔─▄ąįūŅ┤¾Ą─╣└ėŗ(j©¼)Ą├╩Ū“┴ó¾wę╗╣P«ŗ”ĪŻ
│ŻęÄ(gu©®)Ą─ŲĮ├µę╗╣P«ŗū„×ķć°(gu©«)┬ō(li©ón)┐╝Ą─�,Ż┐╝Ņ}ą═,Ż¼┤¾▓┐Ęųéõ┐╝┐╝╔·ī”(du©¼)Ųõ▓ó▓╗─░╔·Ż¼Ūę╚AłDĮ╠ė²ę▓┐éĮY(ji©”)┴╦┐ņ╦┘┼ąöÓę╗╣P«ŗĄ─ā╔éĆ(g©©)▒žéõŚl╝■——ó┘łDą╬×ķš¹¾w;ó┌łDą╬Ųµ³c(di©Żn)öĄ(sh©┤)×ķ0╗“2,ĪŻ╚ń╣¹īóę╗╣P«ŗ┐╝³c(di©Żn)▀\(y©┤n)ė├į┌┴ó¾włDųą,Ż¼╔Ž╩÷┼ąöÓ╝╝Ū╔╩Ūʱę└╚╗│╔┴ó─ž?┤░Ė╩Ū┐ŽČ©Ą─!ę└╚╗▀mė├ĪŻ¤ošō╩ŪŲĮ├µłD▀Ć╩Ū┴ó¾włD,Ż¼śŗ(g©░u)Į©ę╗╣P«ŗĄ─ĘĮ╩Įų╗ėąā╔ĘNŻ║ę╗,ĪóŲ╣P³c(di©Żn)║═┬õ╣P³c(di©Żn)▓╗ųžÅ═(f©┤)Ż¼╣╩┤µį┌ā╔éĆ(g©©)Ųµ³c(di©Żn),Ż¼▀@Įą“ėą╩╝ėąĮK”;Č■,ĪóŲ╣P³c(di©Żn)║═┬õ╣P³c(di©Żn)ųžÅ═(f©┤)Ż¼╣╩▓╗┤µį┌Ųµ³c(di©Żn),Ż¼▀@Įą“╩╝ĮK╚ńę╗”,ĪŻ
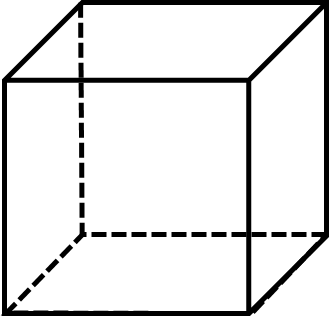
└²╚ńŻ¼╔ŽłD×ķš²┴∙├µ¾w,Ż¼╣▓ėą╩«Č■Śl└ŌŠĆ,Ż¼─Ū├┤╩Ūʱ─▄ē“ę╗┤╬ąį▓╗ųžÅ═(f©┤)Ą─ū▀═Ļ╦∙ėą└ŌŠĆ─ž?š²┴∙├µ¾w×ķš¹¾wŻ¼ĮėŽ┬üĒų▒Įė┼ąöÓŲµ³c(di©Żn)öĄ(sh©┤)╩ŪʱØMūŃ0╗“2╝┤┐╔,ĪŻė╔ė┌š²┴∙├µ¾w╣▓ėą8éĆ(g©©)Ēö³c(di©Żn),Ż¼Ūę├┐ę╗éĆ(g©©)Ēö³c(di©Żn)Č╝░l(f©Ī)╔ó│÷┴╦3Śl└ŌŻ¼╣╩š²┴∙├µ¾wĄ─Ųµ³c(di©Żn)öĄ(sh©┤)×ķ8Ż¼▓╗ØMūŃ╔Ž╩÷▒žę¬Śl╝■,Ż¼▓╗─▄ę╗╣P«ŗ│╔,ĪŻ
ĪŠŅA(y©┤)£y(c©©)Ņ}Ī┐Ž┬├µ──ę╗éĆ(g©©)┴ó¾włDą╬─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└ŌŻ║
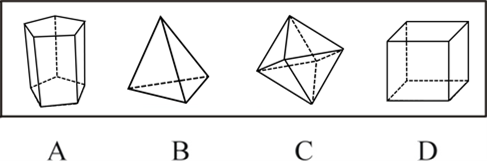
ĪŠĮŌ╬÷Ī┐Ņ}─┐įO(sh©©)å¢×ķ“──ę╗éĆ(g©©)┴ó¾włDą╬─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└Ō”Ż¼╣╩┤╦Ņ}┐╝▓ķ“┴ó¾wę╗╣P«ŗ”,Ż¼└¹ė├ę╗╣P«ŗā╔éĆ(g©©)▒žéõŚl╝■▀M(j©¼n)ąą┼ąöÓŻ║ó┘łDą╬×ķš¹¾w;ó┌łDą╬Ųµ³c(di©Żn)öĄ(sh©┤)×ķ0╗“2,ĪŻė╔ė┌╦∙ėą┴ó¾włDŠ∙×ķš¹¾wŻ¼╣╩ĮėŽ┬üĒ╝Ü(x©¼)ų┬┼ąöÓĖ„łDą╬Ųµ³c(di©Żn)öĄ(sh©┤)╝┤┐╔,ĪŻAĒŚ(xi©żng)×ķ╬Õ└Ōų∙,Ż¼╦∙ėąĒö³c(di©Żn)░l(f©Ī)╔ó└ŌŠĆöĄ(sh©┤)Č╝×ķ3Ż¼Š∙×ķŲµ³c(di©Żn),Ż¼įōłDą╬╣▓ėą10éĆ(g©©)Ųµ³c(di©Żn),Ż¼▓╗─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└ŌŻ¼┼┼│²;BĒŚ(xi©żng)×ķ╚²└ŌÕF,Ż¼╦∙ėąĒö³c(di©Żn)░l(f©Ī)╔ó└ŌŠĆöĄ(sh©┤)Č╝×ķ3,Ż¼Š∙×ķŲµ³c(di©Żn)Ż¼įōłDą╬╣▓ėą4éĆ(g©©)Ųµ³c(di©Żn),Ż¼▓╗─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└Ō,Ż¼┼┼│²;CĒŚ(xi©żng)×ķ░╦├µ¾wŻ¼╦∙ėąĒö³c(di©Żn)░l(f©Ī)╔ó└ŌŠĆöĄ(sh©┤)Č╝×ķ4,Ż¼Č╝▓╗╩ŪŲµ³c(di©Żn),Ż¼įōłDą╬╣▓ėą0éĆ(g©©)Ųµ³c(di©Żn)Ż¼─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└Ō,Ż¼«ö(d©Īng)▀x;DĒŚ(xi©żng)×ķš²┴∙├µ¾w,Ż¼╦∙ėąĒö³c(di©Żn)░l(f©Ī)╔ó└ŌŠĆöĄ(sh©┤)Č╝×ķ3Ż¼Š∙×ķŲµ³c(di©Żn),Ż¼įōłDą╬╣▓ėą8éĆ(g©©)Ųµ³c(di©Żn),Ż¼▓╗─▄ę╗┤╬▓╗ųžÅ═(f©┤)ĄžĮø(j©®ng)▀^╦∙ėą└ŌŻ¼┼┼│²,ĪŻ╣╩įōŅA(y©┤)£y(c©©)Ņ}┤░Ė×ķ▀xĒŚ(xi©żng)C,ĪŻ


ŽÓĻP(gu©Īn)ā╚(n©©i)╚▌═Ų╦]Ż║

┘Ną─┐╝╣½┐═Ę■

┘Ną─īŻī┘┐═Ę■
╔Žę╗Ų¬Ż║2022─Ļ╩Ī┐╝ąą£y(c©©)łDą╬═Ų└Ēų«ØhūųĄ─┐╝³c(di©Żn)
Ž┬ę╗Ų¬Ż║2022─Ļ╩Ī┐╝ąą£y(c©©)éõ┐╝ Ż║ŅÉ▒╚═Ų└ĒųąęūšŲ╬šĄ─ī┘ąįĻP(gu©Īn)ŽĄ

ł¾(b©żo)├¹Śl╝■?
ŹÅ╬╗▀xō±?
╣Pįć┐Ų─┐?
├µįćĘĮ╩Į?
......

 į┌ŠĆ┐═Ę■Ī┴
į┌ŠĆ┐═Ę■Ī┴

³c(di©Żn)ō¶╦∙ąĶ┘Y┴Ž,Ż¼Æ▀┤aŅI(l©½ng)╚Ī








šą┐╝╣½Ėµ┐╝įć┤¾ŠV┬Ü╬╗▒Ēł¾(b©żo)├¹╚ļ┐┌£╩(zh©│n)┐╝ūC┤“ėĪ┐╝įćĢr(sh©¬)ķg│╔┐ā(j©®)▓ķįā├µįć├¹å╬õøė├╣½╩Š┐╝įć┐ņėŹ
ł¾(b©żo)┐╝┴„│╠ł¾(b©żo)┐╝å¢┤ł¾(b©żo)┐╝Śl╝■┬Ü─▄ĮķĮBš■▓▀Ę©ęÄ(gu©®)ł¾(b©żo)┐╝öĄ(sh©┤)ō■(j©┤)Ęų╬÷Üv─Ļ┐╝Ūķ