2021-12-27 11:12:52 ЙЋе(wЈД)TПМдОW(wЈЃng) 
 ЮФеТэ(lЈЂi)дДЃКъЮїЗждК
ЮФеТэ(lЈЂi)дДЃКъЮїЗждК

ѓ(bЈЄo)ПМ(wЈЈn)ю}НтЛѓЃП
ЭЌW(xuЈІ)пДaзЩд(xЈВn)

жБНЧШ§НЧаЮЕФШ§п
щL(zhЈЃng)ЖШЗћКЯЙДЙЩЖЈРэЃК.png) ,ЃЌЗћКЯдЖЈРэЕФГЃгУЙДЙЩЕ(shЈД)ШчЯТБэЫљЪО,ЁЃ
,ЃЌЗћКЯдЖЈРэЕФГЃгУЙДЙЩЕ(shЈД)ШчЯТБэЫљЪО,ЁЃ


ЦфжаЃЌЊ(yЈЉng)гУзюЖрЕФЪЧ3,ЁЂ4,ЁЂ5п@вЛНMМАХcЦфГЩБШР§ъP(guЈЁn)ЯЕЕФЙДЙЩЕ(shЈД)ЃЌР§Шч6,ЁЂ8,ЁЂ10;12ЁЂ16,ЁЂ20ЕШ,ЁЃгзЁп@аЉГЃгУЙДЙЩЕ(shЈД)ЃЌвЛЗНУц,ЃЌзКЮг(jЈЌ)Ыу(wЈЈn)ю}жаЩцМАжБНЧШ§НЧаЮп щL(zhЈЃng)г(jЈЌ)Ыуr(shЈЊ),ЃЌДѓЖрЧщrЯТПЩвдЪЁШЅЧѓЦНЗНщ_(kЈЁi)ЗНЕФЭ(fЈД)ыsг(jЈЌ)ЫуЃЌЪТАыЙІБЖ;СэвЛЗНУц,ЃЌдквЛаЉ(wЈЈn)ю}жа,ЃЌШєФмТ(liЈЂn)ЯЕГЃгУЙДЙЩЕ(shЈД)ЃЌПЩПьЫйЧѓНт,ЁЃЯТУц,ЃЌЮвНY(jiЈІ)КЯзЕРецю}э(lЈЂi)Њ(yЈЉng)гУвЛЯТЁЃ
ЁОР§1ЁПвЛ(gЈЈ)АыAаЮЙАщT(mЈІn)ЕФКЭИпЗжeщ8УзКЭ4Уз,ЃЌвЛнvим(chЈЅ)?yЈЂn)жј?.8Уз,ЁЂУПгИп20РхУзЕФХнФАхЭЈп^(guЈА)дЙАщT(mЈІn)ЁЃШчЙћм(chЈЅ)ЖЗЕзВПХcЕиУцЕФДЙжБОрыxщ1.1Уз,ЃЌ(wЈЈn)вЊЭЈп^(guЈА)ЙАщT(mЈІn),ЃЌУПДЮзюЖрПЩвдбbнdзгХнФАх?
A.9B.10
C.11D.12
ЁОД№АИЁПB
ЁОНтЮіЁПЕквЛВНЃЌБОю}ПМВщзКЮ(wЈЈn)ю},ЃЌйгкЦНУцзКЮю(lЈЈi),ЁЃ
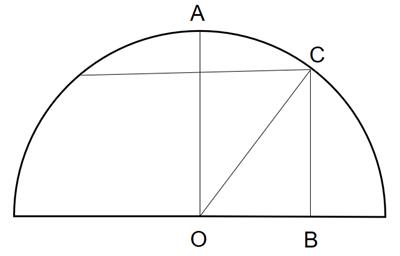
ЕкЖўВНЃЌШчDЫљЪО,ЃЌдкжБНЧШ§НЧаЮOBCжа,ЃЌOC=OA=4УзЃЌ.png) ,ЃЌИљў(jЈД)ЙДЙЩЖЈРэ,ЃЌBC=
,ЃЌИљў(jЈД)ЙДЙЩЖЈРэ,ЃЌBC=.png) ЃЌм(chЈЅ)ЖЗЕзВПХcЕиУцЕФДЙжБОрыxщ1.1УзЃЌХнФАхУПгИп20РхУз,ЃЌ
ЃЌм(chЈЅ)ЖЗЕзВПХcЕиУцЕФДЙжБОрыxщ1.1УзЃЌХнФАхУПгИп20РхУз,ЃЌ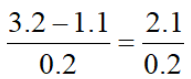 <11,ЃЌМДУПДЮзюЖрПЩвдбbнd10гХнФАхЁЃ
<11,ЃЌМДУПДЮзюЖрПЩвдбbнd10гХнФАхЁЃ
вђДЫ,ЃЌпxёBпxэ(xiЈЄng),ЁЃ
ЁОеf(shuЈ)УїЁПвбжЊOC=4ЃЌOB=2.4,ЃЌІ(duЈЌ)Њ(yЈЉng)ГЃгУЙДЙЩЕ(shЈД)3,ЁЂ4ЁЂ5,ЃЌаБп щL(zhЈЃng)ЖШ4=5×0.8,ЃЌжБНЧп 2.4=3×0.8ЃЌЙЪСэвЛlжБНЧп BC=4×0.8=3.2,�,ЃПЩБмУтЦНЗНдйщ_(kЈЁi)ЗНЕФЭ(fЈД)ыsг(jЈЌ)ЫуЁЃ
Г§СЫдкжБНЧШ§НЧаЮг(jЈЌ)ЫужаТ(liЈЂn)ЯЕЙДЙЩЕ(shЈД)ПЩПьЫйЧѓНт,ЃЌГЃгУЙДЙЩЕ(shЈД)пПЩгУгкЗћКЯ.png) аЮЪНЕФЛљБОг(jЈЌ)Ыужа,ЁЃ
аЮЪНЕФЛљБОг(jЈЌ)Ыужа,ЁЃ
ЁОР§2ЁПАбвЛ(gЈЈ)е§ЗНаЮЕФЫФ(gЈЈ)НЧЗжeЧаГ§вЛ(gЈЈ)ЕШбќШ§НЧаЮЃЌЪЃЯТвЛ(gЈЈ)щL(zhЈЃng)ВЛЕШЕФОиаЮ,ЁЃШєБЛЧаГ§ВПЗжЕФПУцЗeщ400ЦНЗНРхУз,ЃЌЧвЧаГ§ЕФШ§НЧаЮЕФжБНЧп ЕФщL(zhЈЃng)ЖШОљщећЕ(shЈД)ЃЌtЫљЪЃОиаЮЕФУцЗeщЖрЩйЦНЗНРхУз?
A.320B.336
C.360D.384
E.400F.420
G.441H.464
ЁОД№АИЁПD
ЁОНтЮіЁПЕквЛВН,ЃЌБОю}ПМВщзКЮ(wЈЈn)ю}ЃЌйгкЦНУцзКЮю(lЈЈi),ЁЃ
ЕкЖўВН,ЃЌдO(shЈЈ)ЩНMЕШбќШ§НЧаЮЕФбќщL(zhЈЃng)ЗжeщxЁЂy,ЃЌtЧаГ§ВПЗжУцЗeщ.png) ,ЃЌЛЏК(jiЈЃn)ЕУ
,ЃЌЛЏК(jiЈЃn)ЕУ.png) ЃЌНтЕУx=12,ЃЌy=16,ЁЃ
ЃЌНтЕУx=12,ЃЌy=16,ЁЃ
ЕкШ§ВНЃЌЙЪSОиаЮ=Sе§ЗНаЮ-SЧаГ§ВПЗж=.png) ,ЁЃ
,ЁЃ
вђДЫ,ЃЌпxёDпxэ(xiЈЄng)ЁЃ
ЁОеf(shuЈ)УїЁПБОю}ШєжБНгИљў(jЈД).png) г(jЈЌ)Ыуx,ЁЂyЕФШЁжЕtп^(guЈА)гкЭ(fЈД)ыs,ЃЌЖјДЫЪНЗћКЯЙДЙЩЖЈРэЕФаЮЪНЃЌПЩ(yЈu)ЯШПМ]Т(liЈЂn)ЯЕГЃгУЙДЙЩЕ(shЈД)ЧѓНт,ЁЃ
г(jЈЌ)Ыуx,ЁЂyЕФШЁжЕtп^(guЈА)гкЭ(fЈД)ыs,ЃЌЖјДЫЪНЗћКЯЙДЙЩЖЈРэЕФаЮЪНЃЌПЩ(yЈu)ЯШПМ]Т(liЈЂn)ЯЕГЃгУЙДЙЩЕ(shЈД)ЧѓНт,ЁЃ
ЁОР§3ЁПп щL(zhЈЃng)щећЕ(shЈД)ЧвГЩЕШВюЕ(shЈД)СаЕФШ§(gЈЈ)е§ЗНаЮ,ЃЌУцЗeжЎКЭВЛДѓгк5000,ЃЌЦфжагаЩ(gЈЈ)е§ЗНаЮЕФУцЗeжЎКЭЕШгкЕк3(gЈЈ)е§ЗНаЮЕФУцЗeЃЌп@гЕФе§ЗНаЮДцдкЖрЩйНM?
A.6B.7
C.9D.10
ЁОД№АИЁПD
ЁОНтЮіЁПЕквЛВН,ЃЌБОю}ПМВщзКЮ(wЈЈn)ю},ЁЃ
ЕкЖўВНЃЌдO(shЈЈ)Ш§(gЈЈ)е§ЗНаЮп щL(zhЈЃng)Зжeщa-n,ЁЂa,ЁЂa+n(aЁЂnЖМЪЧе§ећЕ(shЈД)),ЃЌФЧУДгЩю}втгаЃК(a-n)²+a²=(a+n)²,ЃЌЛЏК(jiЈЃn)щa²=4anЃЌгЩгкaще§ећЕ(shЈД)ПЩжЊa=4n,�,ЃПЩжЊШ§(gЈЈ)е§ЗНаЮп щL(zhЈЃng)Зжeщ3nЁЂ4n,ЁЂ5n,ЃЌУцЗeжЎКЭщ(3n)²+(4n)²+(5n)²=50n²≤5000ЃЌn²≤100,ЃЌnПЩвдШЁ1ЕН10,ЃЌЙВ10НMНтЁЃ
вђДЫ,ЃЌпxёDпxэ(xiЈЄng),ЁЃ
ЁОеf(shuЈ)УїЁПШєШ§(gЈЈ)е§ЗНаЮп
щL(zhЈЃng)Зжeгщa,b,cЃЌИљў(jЈД)ю}втЦфУцЗeЗћКЯ.png) ,ЃЌtШЁжЕ(yЈu)ЯШПМ]ГЃгУЙДЙЩЕ(shЈД),ЃЌгжИљў(jЈД)“п
щL(zhЈЃng)щећЕ(shЈД)ЧвГЩЕШВюЕ(shЈД)Са”ЃЌHЙДЙЩЕ(shЈД)3,ЁЂ4,ЁЂ5МАХcЦфГЩБШР§ъP(guЈЁn)ЯЕЕФЕ(shЈД)зжЗћКЯЁЃУцЗeжЎКЭВЛДѓгк5000,ЃЌt
,ЃЌtШЁжЕ(yЈu)ЯШПМ]ГЃгУЙДЙЩЕ(shЈД),ЃЌгжИљў(jЈД)“п
щL(zhЈЃng)щећЕ(shЈД)ЧвГЩЕШВюЕ(shЈД)Са”ЃЌHЙДЙЩЕ(shЈД)3,ЁЂ4,ЁЂ5МАХcЦфГЩБШР§ъP(guЈЁn)ЯЕЕФЕ(shЈД)зжЗћКЯЁЃУцЗeжЎКЭВЛДѓгк5000,ЃЌt.png) ,ЁЃcЕФШЁжЕщ5ЕФБЖЕ(shЈД)ЧваЁгкЕШгк50ЃЌЙВ50÷5=10(gЈЈ),ЃЌЙЪЗћКЯlМўЕФЙВ10НM,ЁЃ
,ЁЃcЕФШЁжЕщ5ЕФБЖЕ(shЈД)ЧваЁгкЕШгк50ЃЌЙВ50÷5=10(gЈЈ),ЃЌЙЪЗћКЯlМўЕФЙВ10НM,ЁЃ
вдЩЯОЭЪЧГЃгУЙДЙЩЕ(shЈД)дкЕ(shЈД)СПъP(guЈЁn)ЯЕжаЕФЊ(yЈЉng)гУЃЌаЁЛяАщгзЁЦфЊ(yЈЉng)гУЧщr,ЃЌдкКѓРm(xЈД)Нтю}жаПЩвдИќПьЫйЕФЕУГіНY(jiЈІ)Йћ,ЁЃ
ЁОаЁНY(jiЈІ)ЁП

ЯръP(guЈЁn)Ш(nЈЈi)ШнЭЦЫ]ЃК

йNаФПМЙЋПЭЗў

йNаФЃ(zhuЈЁn)йПЭЗў
ЩЯвЛЦЊЃК2022ЪЁПМйYСЯЗжЮіфПМг(jЈЌ)жЎКЛ(shЈЊ)ЛљЕA(chЈГ)
ЯТвЛЦЊЃК2022ФъЪЁПМааy(cЈЈ)ГЃзR(shЈЊ)ЃКЙЋПМжаЕФжај(guЈЎ)ЙХДњЮФЛЏЁЊЁЊСМфОЮФЛЏ

2023АцШADНЬФукAУцдЯЕСа Вј(shЈБ)ЙЋе(wЈД)TУцдШADЃ(zhuЈЁn)МвдНт1000ю}ЃЈ3БОЬзЃЉ

2023АцНЮїЙЋе(wЈД)T4БОЬз+ЩъеН(jЈЉng)ЕфЗЖЮФ50ЦЊ+ааy(cЈЈ)ИпюlПМќc(diЈЃn) 6БО

2023КгББЙЋе(wЈД)Tааy(cЈЈ)+ЩъеюA(yЈД)y(cЈЈ)дОэ2БО

ЙЋПМПкДќј(shЈБ)10БОЃЈааy(cЈЈ)+ЩъеЃЉ

ѓ(bЈЄo)УћlМў?
ЮЛпxё?
ЙPдПЦФП?
УцдЗНЪН?
......

 дкО(xiЈЄn)ПЭЗўЁС
дкО(xiЈЄn)ПЭЗўЁС

ќc(diЈЃn)єЫљашйYСЯ,ЃЌпДaюI(lЈЋng)ШЁ








еаПМЙЋИцПМдДѓОVТЮЛБэѓ(bЈЄo)УћШыПкЪ(zhЈГn)ПМзCДђгЁПМдr(shЈЊ)щgГЩП(jЈЉ)Вщд(xЈВn)УцдУћЮфгУЙЋЪОПМдПьг
ѓ(bЈЄo)ПМСїГЬѓ(bЈЄo)ПМ(wЈЈn)Д№ѓ(bЈЄo)ПМlМўТФмНщНBеўВпЗЈв(guЈЉ)ѓ(bЈЄo)ПМЕ(shЈД)ў(jЈД)ЗжЮіvФъПМЧщ
Е(shЈД)СПъP(guЈЁn)ЯЕбдеZ(yЈГ)РэНтХарЭЦРэйYСЯЗжЮіГЃзR(shЈЊ)Харааy(cЈЈ)ММЧЩ