2021-12-23 11:39:32 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәЛДҙЁ·ЦФә
ОДХВҒнФҙЈәЛДҙЁ·ЦФә

Ҳу(bЁӨo)ҝјҶ–о}Ҫв»у,Јҝ
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

ФЪЛДҙЁКЎ№«„Х(wЁҙ)ҶTҝјФҮЦР,Ј¬ҺЧәОҶ–о}Т»ЦұКЗҝјФҮөДЧоҙуҹбйTҝјьc(diЁЈn)Ц®Т»,Ј¬ФЪ”ө(shЁҙ)БҝкP(guЁЎn)ПөөДҝјФҮо}ДҝЦРУРЕeЧгЭpЦШөДөШО»ЎЈҺЧәОФЪҝјФҮЦРөДЦчТӘо}РНһйЈәҺЧәОУӢ(jЁ¬)Лг,ЎўҺЧәОМШРФ,ЎўҺЧәОҳӢ(gЁ°u)ФмЎЈЯ@Иэ·NоҗРНКЗФЪҝјФҮЦРЧооl·ұіц¬F(xiЁӨn)өДҝјФҮоҗРН,ЎЈ
ФЪЯ@Иэ·Nо}ДҝоҗРНАпГжЧоРиТӘ„“(chuЁӨng)РВЛјҫSөДҫНКЗҺЧәОҳӢ(gЁ°u)Фм,Ј¬Я@Т»оҗРНөДо}ДҝРиТӘОТӮғНЁЯ^ЧФјәөДҝХйgЛјҫSИҘ„“(chuЁӨng)ФмТ»·NҲDРОөДЖҙңҗ·ҪКҪЈ¬ЧҢОТӮғҳӢ(gЁ°u)ФміцҒнөДҺЧәОҲD°ё·ыәПо}ёЙөДТӘЗу,Ј¬ІўЗТқMЧгТ»Р©ЖдЛы—lјю,ЎЈТӘЗуФЪҳӢ(gЁ°u)ФміцөДТ»ПөБРҲD°ёЦРҢЩУЪЧојСҳӢ(gЁ°u)ФмЈ¬К№өГЦЖЧчіЙұҫЧоөН»тХЯКЗАЛЩM(fЁЁi)ІДБПЧоЙЩөИ,ЎЈЛщТФФЪОТӮғЧцҳӢ(gЁ°u)Фмоҗо}ДҝРиТӘҙујТҙтй_ДX¶ҙ,Ј¬ө«КЗТ»¶ЁТӘУӣөГКЧТӘЗ°Мб,Ј¬ҫНКЗ·ыәПо}ёЙТӘЗуЈ¬ФЪҙЛЗ°МбПВ,Ј¬ЧҢОТӮғөД·Ҫ°ёЯ_(dЁў)өҪЧојСјҙҝЙ,ЎЈ
ҺЧәОҳӢ(gЁ°u)Фмоҗо}ДҝФЪҝјФҮЦРЈ¬іЈіЈЕдәПОТӮғТ»Р©МШКвөДҺЧәОРФЩ|(zhЁ¬)іцо},Ј¬АэИзЈә№ҙ№Й¶ЁАн,ЎўҺЧәОЧоЦөАнХ“ЎўғЙьc(diЁЈn)Ц®йgЦұҫҖЧо¶МөИТ»Р©іЈТҠөДҺЧәОРФЩ|(zhЁ¬),Ј¬ЕдәПФЪТ»Жр,Ј¬ЧҢо}Дҝп@өГёьјУУРЙо¶ИәНлy¶ИЎЈЛщТФ,Ј¬ОТӮғФЪЧцҙЛоҗо}ДҝөДЯ^іМЦР,Ј¬ЕдәПЦ®З°ЛщҢW(xuЁҰ)Я^өДҺЧәОРФЩ|(zhЁ¬)Х№й_ЛјҝјЈ¬•юҪoН¬ҢW(xuЁҰ)ӮғҺ§ҒнІ»Т»ҳУөДЛјВ·,Ј¬ЙхЦБУЪКЗОТӮғЖЖо}өДкP(guЁЎn)жIЛщФЪ,ЎЈ
ҪУПВҒнОТӮғҝҙғЙӮҖАэо}Јә
ЎҫАэ1ЎҝДіөШКР…^(qЁұ)УРТ»ӮҖйL·ҪРОҸVҲцЈ¬ЖдГж·eһй1600ЖҪ·ҪГЧ,ЎЈУЙҙЛҝЙЦӘ,Ј¬Я@ӮҖҸVҲцөДЦЬйLЦБЙЩУРЈә
A.160ГЧB.200ГЧ
C.240ГЧD.320ГЧ
Ўҫҙр°ёЎҝA
ЎҫҪвОцЎҝҪв·ЁТ»ЈәөЪТ»ІҪЈ¬ұҫо}ҝјІйҺЧәОҶ–о},Ј¬ҢЩУЪҺЧәОМШКвРФЩ|(zhЁ¬)оҗ,ЎЈ
өЪ¶юІҪЈ¬ФO(shЁЁ)йL·ҪРОөДйLһйxГЧ,Ј¬Ң’һйГЧ,Ј¬„tйL·ҪРОөДЦЬйLһй2(x+![]() )ГЧЎЈ
)ГЧЎЈ
өЪИэІҪ,Ј¬ёщ“ю(jЁҙ)ҫщЦөІ»өИКҪ¶ЁАнЈ¬a+b≥2,Ј¬abТ»¶Ё,Ј¬ФЪa=b•rЈ¬a+bЧоРЎ,ЎЈ®”(dЁЎng)x=![]() •r,Ј¬јҙx=40•rЈ¬ЦЬйLЧоРЎ,Ј¬ЧоРЎЦөһй2×(40+)=160(ГЧ),ЎЈ
•r,Ј¬јҙx=40•rЈ¬ЦЬйLЧоРЎ,Ј¬ЧоРЎЦөһй2×(40+)=160(ГЧ),ЎЈ
Ҫв·Ё¶юЈәөЪТ»ІҪЈ¬ұҫо}ҝјІйҺЧәОҶ–о},Ј¬ҢЩУЪҺЧәОМШКвРФЩ|(zhЁ¬)оҗ,ЎЈ
өЪ¶юІҪ,Ј¬ёщ“ю(jЁҙ)ҺЧәОМШРФЈ¬йL·ҪРОГж·eТ»¶Ё,Ј¬ФҪҪУҪьУЪХэ·ҪРО•rЦЬйLФҪРЎ,Ј¬ұҫо}ҝЙЦұҪУһйХэ·ҪРОЈ¬„tХэ·ҪРОЯ…йLһй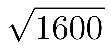 =40(ГЧ),Ј¬ЦЬйLһй4×40=160(ГЧ),ЎЈ
=40(ГЧ),Ј¬ЦЬйLһй4×40=160(ГЧ),ЎЈ
ТтҙЛЈ¬Яx“сAЯxн—(xiЁӨng),ЎЈ
ЎҫАэ2ЎҝТ»ӮҖжЯЧУ(јҙДў№Ҫ·NЧУ)ВдФЪдҒЙП IрB(yЁЈng)НБөДйL·ҪРО»ЁЕи(йL40АеГЧ,Ј¬Ң’30АеГЧ)ЦРСлЈ¬ОьКХНБИА IрB(yЁЈng)Іўй_КјЙъйL,ЎЈжЯЧУйLіЙДў№ҪРиТӘ7Мм,Ј¬ФЩҪӣ(jЁ©ng)Я^3МмЈ¬Дў№ҪіЙКм,Ј¬ҫН•юСШЕcЛ®ЖҪГжіЙ45¶ИҪЗөД·ҪПтПтПВҮҠЙджЯЧУ,ЎЈјЩФO(shЁЁ)жЯЧУТ»ҪУУ|НБИАҫНй_КјЙъйLЈ¬Дў№ҪөДҫъЙwКЗ°лҸҪһй3АеГЧөДҲAұP,Ј¬Дў№ҪёЯ10АеГЧ,Ј¬ҫъ—U°лҸҪһй1АеГЧЈ¬ЗТДў№ҪІ»•юЛАНц,Ј¬Ҷ–Дў№ҪйLқMХыӮҖ»ЁЕиРиТӘ¶аЙЩМм?
A.30B.37
C.40D.47
Хэҙ_ҙр°ёЈәA
ҪвОц
өЪТ»ІҪ,Ј¬ұҫо}ҝјІйҺЧәОҶ–о}Ј¬ҢЩУЪЖдЛыҺЧәОоҗ,ЎЈ
өЪ¶юІҪ,Ј¬ё©Т•ҲDИзПВЛщКҫЈ¬ёщ“ю(jЁҙ)№ҙ№Й¶ЁАнҝЙөГйL·ҪРО»ЁЕиөДҢҰҪЗҫҖйL¶Иһй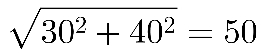 (АеГЧ),Ј¬ДЗГҙЖріхөДТ»ӮҖжЯЧУҫалx»ЁЕиөДЧоЯh(yuЁЈn)¶Лһй(АеГЧ),ЎЈ
(АеГЧ),Ј¬ДЗГҙЖріхөДТ»ӮҖжЯЧУҫалx»ЁЕиөДЧоЯh(yuЁЈn)¶Лһй(АеГЧ),ЎЈ
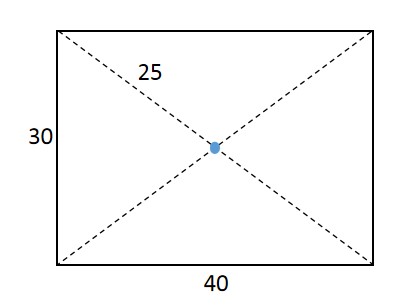
өЪИэІҪЈ¬ИзПВҲDЛщКҫ,Ј¬Из№ыөҪЯ_(dЁў)»ЁЕиЧоЯh(yuЁЈn)¶Л,Ј¬ҸДй_КјөҪДў№ҪйLқM№ІҪӣ(jЁ©ng)ҡvБЛғЙҙОжЯЧУҮҠЙдәНөЪИэҙОДў№ҪЙъйLЯ^іМЎЈ
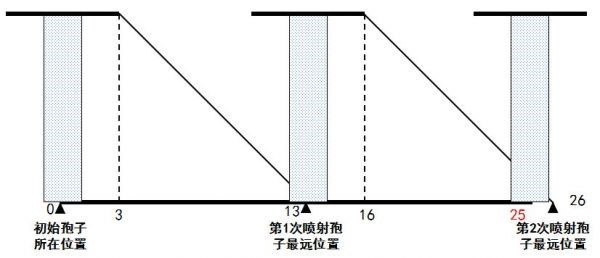
өЪЛДІҪ,Ј¬ГҝТ»ҙОДў№ҪөДЙъйLЯ^іМ•rйgһй7+3=10(Мм),Ј¬ДЗГҙғЙҙОжЯЧУҮҠЙдәНөЪИэҙОДў№ҪЙъйLөД•rйgһй2×10+7=27(Мм)ЎЈӣ]УРЯxн—(xiЁӨng),Ј¬„tЯx“сҙуУЪ27ЗТЧоҪУҪьөДМм”ө(shЁҙ),ЎЈ
ТтҙЛЈ¬Яx“сAЯxн—(xiЁӨng),ЎЈ
НЁЯ^ТФЙПғЙӮҖАэо}ОТӮғҝЙТФ°l(fЁЎ)¬F(xiЁӨn),Ј¬ФЪЧцо}өДЯ^іМЦР,Ј¬ЕдәПҺЧәОіЈТҠөДМШРФИҘХ№й_ҺЧәОҳӢ(gЁ°u)ФмөДЛјҝјЈ¬Из»ўМнТн,Ј¬Я@ҳУөД·Ҫ·ЁДгҢW(xuЁҰ)•юБЛҶб?

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

Ҳу(bЁӨo)Гы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc(diЁЈn)“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲу(bЁӨo)ГыИлҝЪңК(zhЁіn)ҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ