2021-12-21 17:01:33 ╣½äš(w©┤)åT┐╝įćŠW(w©Żng) 
 ╬─š┬üĒį┤Ż║įŲ─ŽĘųį║
╬─š┬üĒį┤Ż║įŲ─ŽĘųį║
į┌ąą£yöĄ(sh©┤)┴┐ĻP(gu©Īn)ŽĄĄ─īW┴Ģ▀^│╠ųąŻ¼įSČÓąĪ╗’░ķī”ė┌ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņ▀@ę╗ŅÉŅ}ą═Ą─šŲ╬š╚į╚╗ėą╦∙ŪĘ╚▒Ż¼ŲõīŹ┤╦ŅÉŅ}ą═Ą─ĮŌĘ©ŽÓī”╣╠Č©,Ż¼ąĪ╗’░ķų╗ę¬Įø(j©®ng)▀^ę╗Č©Ą─ŠÜ┴ĢŠ═─▄╩ņŠÜšŲ╬šĪŻ╦∙ęįĮ±╠ņ╬ęéāę╗ŲīW┴ĢŽ┬░╔,ĪŻ
į┌īW┴ĢČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņūŅķ_╩╝,Ż¼╩ūŽ╚ę¬ī”┤╦ŅÉŅ}ą═ėą│§▓ĮĄ─┴╦ĮŌĪŻ┤╦ŅÉŅ}ą═Üwī┘ė┌╝»║Žå¢Ņ},Ż¼╝┤╚▌│Ōå¢Ņ};╚╗Č°╦³ėų╚┌║Ž┴╦śOųĄĄ─╦╝Žļ,Ż¼ąĶę¬═¼īWéāė├ūŅųĄ╦╝ŠS╚źĮŌŅ}ĪŻ═©│ŻČ°čį,Ż¼┤╦ŅÉŅ}ą═Ģ■│÷¼F(xi©żn)ĻP(gu©Īn)µIį~“Č╝……ų┴╔┘……”,Ż¼╝┤ę¬Ū¾═¼ĢrØMūŃČÓĘNŚl╝■Ą─ŪķøröĄ(sh©┤)Ż¼Žļ▐kĘ©Ū¾įōŪķøröĄ(sh©┤)Ą─śOųĄ,ĪŻ╬─ūų▒╚▌^│ķŽ¾,Ż¼╬ęéā«ŗ│÷łDüĒÄ═ų·┤¾╝ęĖ³║├Ąž└ĒĮŌĪŻ
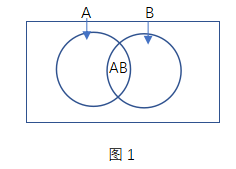
ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņŅÉĄ─Ņ}─┐Š═Ž±╔ŽłD(łD1)╦∙╩Š,Ż¼═©│ŻĢ■ūī╬ęéāŪ¾Ą─╩Ū═¼ĢrØMūŃČÓéĆŚl╝■Ą─ģ^(q©▒)ė“Ą─śOųĄ,Ż¼▒╚╚ń┤╦Ņ}Š═╩Ūå¢ABĄ─ūŅąĪųĄ×ķČÓ╔┘ĪŻį┌łDą╬ųą,Ż¼AB┤·▒ĒĄ─ģ^(q©▒)ė“╩Ūā╔éĆ╝»║ŽŽÓĮ╗Ą─▓┐Ęų,Ż¼Å─łDųą┐╔ęį┐┤│÷Ż¼ā╔éĆ╝»║Ž“ļxĄ├įĮķ_,Ż¼ABģ^(q©▒)ė“įĮąĪ”Ż¼▐D(zhu©Żn)╗»×ķöĄ(sh©┤)īWšZčį╝┤Ū¾Ą─╩Ūā╔éĆ╝»║ŽĮ╗╝»Ą─ūŅąĪųĄ,ĪŻ╚ń╣¹Ņ}─┐ø]ėąŽ▐ųŲ,Ż¼ā╔éĆ╝»║Ž╗źŽÓ¬Ü┴óĄ─Ģr║“Ż¼įōĮ╗╝»Ą─ūŅąĪųĄŠ═×ķ0┴╦,ĪŻĄ½╩Ūę╗░ŃŪķørŽ┬,Ż¼Ņ}─┐ųąā╔éĆ╝»║ŽČ╝Ģ■ėąĮ╗╝»Ż¼╦∙ęį▀@éĆĢr║“╬ęéāŠ═▓╗╠½╚▌ęūÅ─š²├µī”ABĄ─śOųĄ▀Mąą┴┐╗»,Ż¼ę“┤╦╬ęéāąĶę¬▐D(zhu©Żn)ūā╦╝ŠS,Ż¼Å─Ę┤ĘĮŽ“╚ź╠ĮėæABĄ─śOųĄĪŻ
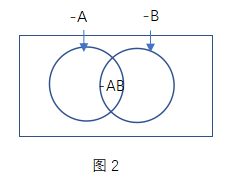
╚ń╔ŽłD(łD2)╦∙╩Š,Ż¼╬ęéāį┘┐┤▀@éĆ╝»║Ž,Ż¼Ęųäe┤·▒Ēų°▓╗ØMūŃAĄ─ŪķøröĄ(sh©┤)ęį╝░▓╗ØMūŃBĄ─ŪķøröĄ(sh©┤),Ż¼š²ųąķgĄ─Į╗╝»×ķ═¼Ģr▓╗ØMūŃA║═BĄ─ŪķøröĄ(sh©┤)Ż¼─Ū├┤ā╔éĆ╝»║ŽĮM║ŽŲüĒĄ─łDą╬┤·▒Ēų°╩▓├┤─ž?╦³æ¬(y©®ng)įō┤·▒Ēų°“▓╗ØMūŃA╗“š▀▓╗ØMūŃBĄ─ŪķøröĄ(sh©┤)”,ĪŻČ°┐š░ūĄ─▓┐Ęų,Ż¼╩Ū“▓╗ØMūŃA╗“▓╗ØMūŃBĄ─ŪķøröĄ(sh©┤)”Ą─Ę┤├µŻ¼╝┤“═¼ĢrØMūŃA║═BĄ─ŪķøröĄ(sh©┤)”——ABĄ─ŪķøröĄ(sh©┤),ĪŻ┤╦ĢrŽļŪ¾ABĄ─ūŅąĪųĄŠ═║åå╬įSČÓ┴╦Ż║ų╗ę¬╩╣“▓╗ØMūŃA╗“š▀BĄ─ŪķøröĄ(sh©┤)”▒M┴┐Ąž┤¾,Ż¼▀@Ģr║“ABĄžųĄŠ═ŽÓī”ūāąĪĪŻį┌-A║═-B▀@ā╔éĆ╝»║Ž¤oĮ╗╝»Ą─Ģr║“,Ż¼ABėąūŅąĪųĄ,Ż¼╚ńŽ┬łD(łD3)╦∙╩ŠĪŻ
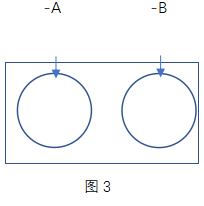
┤╦Ģr╬ęéāŽļŪ¾ABĄ─ūŅąĪųĄ,Ż¼ų╗ąĶė├┐éĄ─ŪķøröĄ(sh©┤)£p╚źĘ┤Ž“śŗ(g©░u)įņ│÷Ą─╝»║Žų«║═Š═ąą┴╦,Ż¼╝┤![]() ĪŻ═©▀^┤╦Ņ},Ż¼┐╔ęįÜw╝{│÷ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņĄ─ĮŌŅ}▓Į¾EŻ║Ę┤Ž“——Ū¾║═——ū÷▓Ņ,ĪŻų«║¾╬ęéāį┌ė÷ĄĮ┤╦ŅÉŅ}ą═Ż¼╬ęéāų╗ąĶę¬░┤šš▀@╚²▓Į,Ż¼Š═┐╔ęįĮŌŅ},ĪŻ
ĪŻ═©▀^┤╦Ņ},Ż¼┐╔ęįÜw╝{│÷ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņĄ─ĮŌŅ}▓Į¾EŻ║Ę┤Ž“——Ū¾║═——ū÷▓Ņ,ĪŻų«║¾╬ęéāį┌ė÷ĄĮ┤╦ŅÉŅ}ą═Ż¼╬ęéāų╗ąĶę¬░┤šš▀@╚²▓Į,Ż¼Š═┐╔ęįĮŌŅ},ĪŻ
║├┴╦Ż¼ŽÓą┼ąĪ╗’░ķéāęčĮø(j©®ng)─”╚Ł▓┴šŲ┴╦,Ż¼╬ęéā┌sŠoė├└²Ņ}üĒÖz“×ę╗Ž┬īW┴ĢĄ─ā╚(n©©i)╚▌░╔,ĪŻ
ĪŠ└²Ī┐─│ÖCśŗ(g©░u)ī”╚½▀\Ģ■╩šęĢŪķør▀Mąąš{(di©żo)▓ķŻ¼į┌1000├¹╩▄įLš▀ųą,Ż¼ė^┐┤▀^Ų╣┼ęŪ“▒╚┘ÉĄ─š╝87%,Ż¼ė^┐┤▀^╠°╦«▒╚┘ÉĄ─š╝75%Ż¼ė^┐┤▀^╠’ÅĮ▒╚┘ÉĄ─š╝69%,ĪŻ▀@1000├¹╩▄įLš▀ųą,Ż¼Ų╣┼ęŪ“Īó╠°╦«║═╠’ÅĮ▒╚┘ÉČ╝ė^┐┤▀^Ą─ų┴╔┘ėąŻ║Ż║
A. 310╚╦
B. 440╚╦
C. 620╚╦
D. 690╚╦
ĪŠ┤░ĖĪ┐A
ĪŠĮŌ╬÷Ī┐Ą┌ę╗▓Į,Ż¼▒ŠŅ}┐╝▓ķūŅųĄå¢Ņ},Ż¼ī┘ė┌ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņĪŻ
Ą┌Č■▓Į,Ż¼Ė∙ō■(j©┤)ČÓ╝»║ŽĘ┤Ž“śŗ(g©░u)įņĄ─╦╝┬Ę,Ż¼“Ę┤Ž“——Ū¾║═——ū÷▓Ņ”ĪŻ
Ę┤Ž“Ż║╬┤ė^┐┤Ų╣┼ęŪ“▒╚┘ÉĄ─╚╦öĄ(sh©┤)×ķ1000×(1-87%)=130╚╦,Ż¼╬┤ė^┐┤╠°╦«▒╚┘ÉĄ─╚╦öĄ(sh©┤)×ķ1000×(1-75%)=250╚╦,Ż¼╬┤ė^┐┤╠’ÅĮ▒╚┘ÉĄ─╚╦öĄ(sh©┤)×ķ1000×(1-69%)=310╚╦ĪŻ
Ū¾║═Ż║╚²ĘN▒╚┘Éėą╚╦ø]┐┤▀^Ą─ūŅČÓėą130+250+310=690╚╦,ĪŻ
ū÷▓ŅŻ║╚²ĘN▒╚┘ÉČ╝ė^┐┤▀^Ą─ų┴╔┘×ķ1000-690=310╚╦,ĪŻ
ę“┤╦,Ż¼▀xō±A▀xĒŚĪŻ
Į±╠ņĄ─īW┴ĢŠ═Ž╚ĄĮ▀@└’,Ż¼ąĪ╗’░ķŽ┬üĒ▀ĆąĶę¬ČÓū÷ÄūéĆ└²Ņ}ņ¢╣╠ę╗Ž┬┼Č,ĪŻ

ŽÓĻP(gu©Īn)ā╚(n©©i)╚▌═Ų╦]Ż║

┘Ną─┐╝╣½┐═Ę■

┘Ną─īŻī┘┐═Ę■
╔Žę╗Ų¬Ż║2022╩Ī┐╝ąą£yéõ┐╝ų«╗∙Ų┌▒╚ųžėŗ╦Ń╝╝Ū╔
Ž┬ę╗Ų¬Ż║2022─Ļ╩Ī┐╝ąą£yöĄ(sh©┤)┴┐ĻP(gu©Īn)ŽĄąą│╠å¢Ņ}ų«Ż║╗▄ć╔Žś“å¢Ņ}

ł¾├¹Śl╝■?
ŹÅ╬╗▀xō±?
╣Pįć┐Ų─┐?
├µįćĘĮ╩Į?
......

 į┌ŠĆ┐═Ę■Ī┴
į┌ŠĆ┐═Ę■Ī┴

³cō¶╦∙ąĶ┘Y┴ŽŻ¼Æ▀┤aŅI(l©½ng)╚Ī








šą┐╝╣½Ėµ┐╝įć┤¾ŠV┬Ü╬╗▒Ēł¾├¹╚ļ┐┌£╩┐╝ūC┤“ėĪ┐╝įćĢrķg│╔┐ā▓ķįā├µįć├¹å╬õøė├╣½╩Š┐╝įć┐ņėŹ