2021-12-20 15:31:32 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәЯ|ҢҺ·ЦФә
ОДХВҒнФҙЈәЯ|ҢҺ·ЦФә

ҲуҝјҶ–о}Ҫв»у,Јҝ
Н¬ҢW(xuЁҰ)’ЯҙaЧЙФғ

ЧоҪьУРҢW(xuЁҰ)ҶT·ҙ‘Ә(yЁ©ng),Ј¬ЕЕБРҪMәПКЗ”ө(shЁҙ)БҝкP(guЁЎn)ПөЦРЧолyҢW(xuЁҰ)Б•(xЁӘ)өДТ»Іҝ·ЦБЛ,Ј¬ЖдЛыөДҸДЦӘЧRьcАнҪвЈ¬өҪЧцо}‘Ә(yЁ©ng)УГ¶јұИЭ^нҳАы,Ј¬ЕЕБРҪMәПҫН·В·рКЗМм•шТ»ҳУ,Ј¬ҫНКЗІ»Гч°ЧЎЈДЗОТӮғҪсМмҫНҒнБДТ»БДЕЕБРҪMәПФхГҙҢW(xuЁҰ)Б•(xЁӘ),ЎЈ

ФЪҢW(xuЁҰ)Б•(xЁӘ)ЕЕБРЕЕБРҪMәПЦ®З°ОТӮғТӘПИҢW(xuЁҰ)Б•(xЁӘ)ғЙӮҖФӯАн,Ј¬јУ·ЁФӯАнәНіЛ·ЁФӯАнЎЈ
јУ·ЁФӯАнЈә®”ОТӮғПлЯ_өҪТ»ӮҖДҝҳЛ•r,Ј¬ҝЙТФёщ“ю(jЁҙ)Т»Р©ұШнҡөД—lјю,Ј¬·ЦіЙ¶а·NЗйӣrЯMРРУ‘Х“Ј¬Гҝ·NЗйӣr¶јҝЙТФЯ_өҪДҝҳЛ,Ј¬ЗйӣrЦ®йgӣ]УРУ°н‘,Ј¬ПИ·Ц„eУӢЛгГҝ·NЗйӣrөД·ҪКҪ”ө(shЁҙ)Ј¬НкіЙЧоҪKДҝҳЛөДҝӮЗйӣr”ө(shЁҙ)ҫНКЗҢўГҝ·NЗйӣr”ө(shЁҙ)БҝПајУЎЈ
іЛ·ЁФӯАнЈә®”ОТӮғПлЯ_өҪТ»ӮҖДҝҳЛ•r,Ј¬РиТӘНЁЯ^¶аӮҖІҪуEІЕДЬНкіЙ,Ј¬ГҝӮҖІҪуEИұТ»І»ҝЙЈ¬ІҪуEЦ®йgӣ]УРУ°н‘,Ј¬ПИУӢЛгГҝӮҖІҪуEөД·ҪКҪ”ө(shЁҙ),Ј¬НкіЙЧоҪKДҝҳЛөДҝӮЗйӣr”ө(shЁҙ)ҫНКЗҢўГҝӮҖІҪуE”ө(shЁҙ)БҝПаіЛЎЈ
АнҪвЦ®әу,Ј¬ОТӮғФЩҒнҢW(xuЁҰ)Б•(xЁӘ)ЕЕБРәНҪMәПЎЈЕЕБРЈәҸДnӮҖИЛЦРЯxіцmӮҖИЛ,Ј¬НкіЙТ»јюУРнҳРтөДКВЗй,Ј¬ҝЙТФАнҪвһй“ЕЕк ”Ј¬ГҝӮҖИЛЦ®йgөДО»ЦГИз№ыХ{(diЁӨo)“QКЗІ»Т»ҳУөД,Ј¬УӢЛг·ҪКҪИзПВЈә
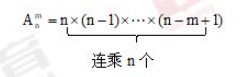
ҪMәПЈәҸДnӮҖИЛЦРЯxіцmӮҖИЛ,Ј¬НкіЙТ»јюӣ]УРнҳРтөДКВЗйЈ¬ҝЙТФАнҪвһй“Яx“с”,Ј¬ЯxіцҒнјҙҝЙ,Ј¬ӣ]УРПИәунҳРтЈ¬ғЙӮҖИЛЦ®йgөДО»ЦГҝЙТФИОТвХ{(diЁӨo)“Q,Ј¬УӢЛг·ҪКҪИзПВЈә
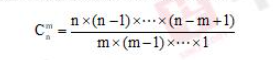
ЦӘөАБЛғЙӮҖФӯАнәН»щөA(chЁі)өДЕЕБРәНҪMәП,Ј¬ОТӮғҫНҝЙТФҪвӣQТ»Іҝ·Ц»щөA(chЁі)өДо}ДҝБЛЎЈОТӮғНЁЯ^Т»өАо}‘Ә(yЁ©ng)УГТ»ПВ,ЎЈ
ЎҫАэЎҝДіКРҸДКРғәНҜ№«Ҳ@өҪКРҝЖјјр^УР6·NІ»Н¬В·ҫҖ,Ј¬ҸДКРҝЖјјр^өҪКРЙЩДкҢmУР5·NІ»Н¬В·ҫҖЈ¬ҸДКРғәНҜ№«Ҳ@өҪКРЙЩДкҢmУР4·NІ»Н¬В·ҫҖ,Ј¬„tҸДКРғәНҜ№«Ҳ@өҪКРЙЩДкҢmөДВ·ҫҖ№ІУРЈә
A.24·NB.36·N
C.34·ND.38·N
Ўҫо}Дҝ·ЦОцЎҝНЁЯ^·ЦОцҝЙТФ°l(fЁЎ)¬F(xiЁӨn),Ј¬о}ёЙөДДҝҳЛКЗҸДКРғәНҜ№«Ҳ@өҪКРЙЩДкҢmЈ¬УРғЙ·NВ·ҫҖҝЙТФЧЯ,Ј¬¶јҝЙТФөҪЯ_ДҝөДөШ,Ј¬ТІҫНКЗХfТӘ·ЦЗйӣrУ‘Х“Ј¬‘Ә(yЁ©ng)УГјУ·ЁФӯАн,Ј¬ЖдЦРУРТ»—lВ·ҫҖРиТӘҪӣ(jЁ©ng)Я^КРҝЖјјр^ІЕДЬөҪЯ_ДҝөДөШ,Ј¬ТІҫНКЗТӘ·ЦІҪуEЯMРРЈ¬ИұТ»І»ҝЙ,Ј¬‘Ә(yЁ©ng)УГіЛ·ЁФӯАн,ЎЈ
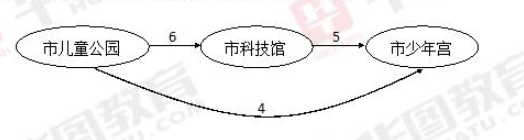
ЎҫҪвОцЎҝөЪТ»·NЗйӣrҸДКРғәНҜ№«Ҳ@ЦұЯ_КРЙЩДкҢmЈ¬№ІУР4—lВ·ҫҖ,Ј¬Яx“сТ»—l·Ҫ·ЁУР·N;өЪ¶ю·NЗйӣrПИөҪКРҝЖјјр^,Ј¬И»әуөҪКРЙЩДкҢmЈ¬өЪТ»ІҪ№ІУР6—lВ·ҫҖЈ¬Яx“сТ»—l·Ҫ·ЁУР·N,Ј¬өЪ¶юІҪ№ІУР5—lВ·ҫҖ,Ј¬‘Ә(yЁ©ng)УГіЛ·ЁФӯАнЈ¬өЪ¶ю·NЗйӣrУР30·N,Ј¬Чоәу‘Ә(yЁ©ng)УГјУ·ЁФӯАн,Ј¬№І34·NЎЈТтҙЛ,Ј¬Яx“сCЯxн—,ЎЈ

НЁЯ^Я@өАо}ОТӮғҝЙТФҝҙіцЈ¬»щөA(chЁі)өДЕЕБРҪMәПоҗҶ–о},Ј¬ЦчТӘҝјІйјУ·ЁФӯАнәНіЛ·ЁФӯАн,Ј¬ҝЙТФәҶҶОёЕАЁЈә·ЦоҗУ‘Х“УГјУ·ЁЈ¬ҝЙТФГиКцһй“ТӘГҙ……ТӘГҙ……”;·ЦІҪСРҫҝУГіЛ·Ё,Ј¬ҝЙТФГиКцһй“өЪТ»ІҪ……өЪ¶юІҪ……”,ЎЈИ»әуКЗЕЕБРәНҪMәПөД‘Ә(yЁ©ng)УГЈ¬УРнҳРтөДКЗЕЕБР,Ј¬ҹoРтөДКЗҪMәП,ЎЈ
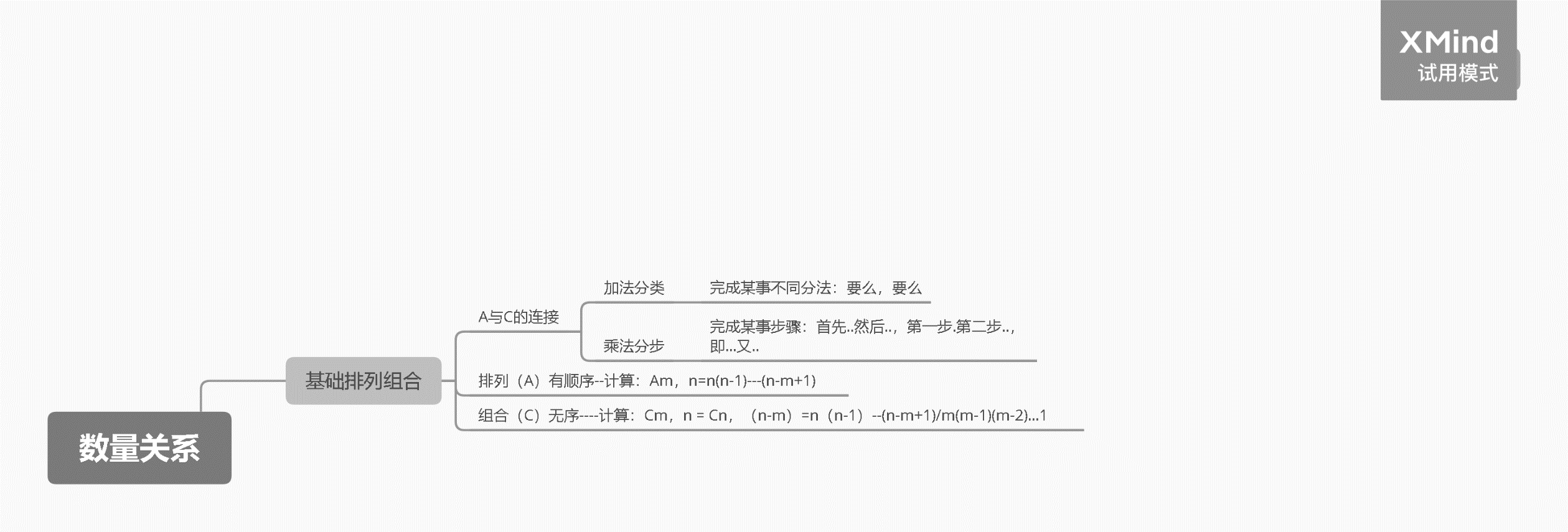
кP(guЁЎn)УЪЕЕБРҪMәПҶ–о}Ј¬КЧПИТӘХЖОХәГғЙӮҖФӯАн,Ј¬И»әуКЗЕЕБРәНҪMәПөД‘Ә(yЁ©ng)УГ,Ј¬НкИ«ХЖОХБЛЦ®әуЈ¬ФЩҢW(xuЁҰ)Б•(xЁӘ)Т»Р©іЈУГјјЗЙ,Ј¬ұИИзЈәІеҝХ·Ё,Ј¬ёф°е·ЁөИөИЈ¬ҸД¶шҪвӣQёь¶аөДҶ–о},ЎЈЕЕБРҪMәПөДҶ–о},Ј¬І»ФЪУЪУӢЛгЈ¬ЦШТӘөДКЗ·ЦОц,Ј¬И»әуҢӨХТХэҙ_өД·Ҫ·Ё,Ј¬ҝмЛЩҪвӣQЎЈ
кP(guЁЎn)УЪЕЕБРҪMәПөДҢW(xuЁҰ)Б•(xЁӘ)·Ҫ·Ё,Ј¬ЯҖУРТ»Р©»щөA(chЁі)ЦӘЧRҫНҪйҪBөҪЯ@,Ј¬ПЈНыҝЙТФҺНЦъҙујТЈ¬Из№ыЯҖУРКІГҙІ»ЗеіюөД,Ј¬ҝЙТФПтОТӮғЧЙФғ,Ј¬•юУРҢЈҳI(yЁЁ)өДАПҺҹҺНЦъҙујТЧРјҡ·ЦОцЈ¬ҙујТјУУН,Ј¬ЧЈҙујТФзИХЙП°¶!

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю
ЙПТ»ЖӘЈә2022ДкКЎҝјРРңy”ө(shЁҙ)БҝкP(guЁЎn)ПөёЕВКҶ–о}әҶҶОСРҫҝ
ПВТ»ЖӘЈә2022ДкКЎҝјРРңyӮдҝјУӢ„қ”ө(shЁҙ)БҝӮдҝјЈ¬·Ҫ·ЁКЗЦЖ„ЩкP(guЁЎn)жI

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ