2021-11-30 10:18:43 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәИAҲDҪМУэ
ОДХВҒнФҙЈәИAҲDҪМУэ
ОТӮғТ»ЙъЦРГҝ•rГҝҝМ¶јФЪЕcеXҙтҪ»өАЈ¬ЛщТФХ„ЖрҪӣ(jЁ©ng)қъ(jЁ¬),Ј¬ПаРЕҙујТІўІ»Д°Йъ,ЎЈө«Д°ЙъөДКЗФЪ№«„Х(wЁҙ)ҶTҝјФҮ®”(dЁЎng)ЦРЈ¬іцо}ИЛ°СТ»ӮҖЙъ»о»ҜөДАэЧУУГҢЈҳI(yЁЁ)Рg(shЁҙ)ХZійПуұнЯ_(dЁў)іцҒн•rҙујТұг•юТ»о^мFЛ®,ЎЈҫНҙЛұҫОДҪoҙујТң\Х„Т»ПВҪӣ(jЁ©ng)қъ(jЁ¬)Ҷ–о}ЦРТ»·NҝҙЛЖёЯ¶Л,Ј¬ҢҚ(shЁӘ)„tҝЙТФГлҡўөДҶ–о}ЈәҪy(tЁҜng)»Iғһ(yЁӯu)»Ҝоҗо}РНХТЧоЦөҶ–о}(ЧоЦөғһ(yЁӯu)»Ҝоҗо}РН)ЎЈ
КЧПИ,Ј¬УыҢW(xuЁҰ)ҙЛ№ҰПИҙтәГ»щұҫ№Ұ,Ј¬¶шХ„ЖрҪӣ(jЁ©ng)қъ(jЁ¬)Ҷ–о}ФхГҙ¶јлxІ»й_АықҷЎўіЙұҫ,ЎўЯM(jЁ¬n)ғr,ЎўКХИлЎўКЫғr,Ўў¶Ёғr,ЎўдNБҝ,ЎўҙтХЫЎўАықҷВКөИЧЦСЫ,ЎЈҙујТФЩјҡ(xЁ¬)Ж·ЖдЦРУРР©БҝөДкP(guЁЎn)ПөЖдҢҚ(shЁӘ)ТІКЗТ»ЦВөД,Ј¬ұИИзКЫғrұҫЩ|(zhЁ¬)ТІҫНКЗДгКХөҪөДеXјҙКХИлЈ¬ЯM(jЁ¬n)ғrЖдҢҚ(shЁӘ)ТІҫНКЗіЙұҫ,ЎЈ®”(dЁЎng)ОТӮғҪY(jiЁҰ)әПОТӮғЙъ»оЦРіЈТҠөДЩIЩuҪ»ТЧ,Ј¬әГПсЯ@Р©БҝОТӮғҫНДЬУГҢЈҳI(yЁЁ)өД”ө(shЁҙ)ҢW(xuЁҰ)ХZСФҒнұнКҫіцҒнЈә

1.Аықҷ=КЫғr(КХИл)-ЯM(jЁ¬n)ғr(іЙұҫ)
2.ҝӮАықҷ=ҶОАықҷ×дNБҝ=(КЫғr-ЯM(jЁ¬n)ғr)×дNБҝ
3.КЫғr=¶Ёғr×ХЫҝЫ
4.АықҷВК=Аықҷ/іЙұҫ(”ө(shЁҙ)БҝкP(guЁЎn)Пө)
ҪУПВҒнЈ¬®”(dЁЎng)ҙујТТСҪӣ(jЁ©ng)ҢҰҪӣ(jЁ©ng)қъ(jЁ¬)Ҷ–о}УРБЛТ»ӮҖіхІҪёРУXЦ®әу,Ј¬ҫoҪУЦшҫНТӘҪoҙујТЙПо}БЛЈә
ЎҫАэ1ЎҝДіЙМЖ·өДЯM(jЁ¬n)ШӣҶОғrһй80ФӘ,Ј¬дNКЫҶОғrһй100ФӘ,Ј¬ГҝМмҝЙКЫіц120јю,Ј¬ТСЦӘдNКЫҶОғrГҝҪөөН1ФӘЈ¬ГҝМмҝЙ¶аКЫіц20јю,ЎЈИфТӘҢҚ(shЁӘ)¬F(xiЁӨn)Ф“ЙМЖ·өДдNКЫАықҷЧоҙу»Ҝ,Ј¬„tдNКЫҶОғr‘Ә(yЁ©ng)ҪөөНөДҪро~КЗЈә
A.5ФӘ
B.6ФӘ
C.7ФӘ
D.8ФӘ
Ўҫҙр°ёЎҝЈәC
ЎҫҪвОцЎҝЈәұҫо}ЛщЗуһйдNКЫҶОғrҪөөН¶аЙЩК№ҝӮАықҷЧоҙуЈ¬ҝЙФO(shЁЁ)дNКЫҶОғrҪөөНxФӘ,Ј¬„tГҝМмҝЙ¶аКЫіц20xјю,Ј¬ёщ“ю(jЁҙ)№«КҪЈәҝӮАықҷ=(КЫғr-ЯM(jЁ¬n)ғr)×дNБҝҝЙөГЈәҝӮАықҷ=(100-x-80)×(120+20x)=(20-x)×(120+20x)ЎЈҙЛо}һйТ»ФӘ¶юҙОәҜ”ө(shЁҙ)ЗуЧоЦө,Ј¬·Ҫ·Ё¶аҳУ»ҜЈә
·ЁТ»ЈәҙъИлЕЕіэ·ЁЗуЧоҙуЦөЈәAЯxн—ҝӮАықҷ=(20-5)×(120+20×5)=3300,Ј¬Н¬АнBЯxн—ҝӮАықҷ=(20-6)×(120+20×6)=3360Ј¬CЯxн—ҝӮАықҷ=(20-7)×(120+20×7)=3380,Ј¬DЯxн—ҝӮАықҷ=(20-8)×(120+20×8)=3360,Ј¬ТтҙЛCЯxн—ЧоҙуЎЈ
·Ё¶юЈәАыУГ¶юҙОәҜ”ө(shЁҙ)РФЩ|(zhЁ¬)ЗуЧоЦө,Ј¬ҝӮАықҷ=-20false+280x+2400,Ј¬ёщ“ю(jЁҙ)¶юҙОәҜ”ө(shЁҙ)РФЩ|(zhЁ¬)Ј¬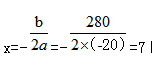 •r,Ј¬әҜ”ө(shЁҙ)ИЎЧоҙуЦөјҙҝӮАықҷЧоҙу;
•r,Ј¬әҜ”ө(shЁҙ)ИЎЧоҙуЦөјҙҝӮАықҷЧоҙу;
·ЁИэЈәАыУГ¶юҙОәҜ”ө(shЁҙ)ҲDПсБгьc(diЁЈn)ЗуЧоЦө,Ј¬ҝӮАықҷ=(20-x)×(120+20x)Ј¬®”(dЁЎng)(20-x)×(120+20x)=0•r,Ј¬x1=20,Ј¬x2=-6Ј¬ҙЛ•rғЙБгьc(diЁЈn)өДЦРьc(diЁЈn)јҙx=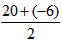 =7•rһйЧоҙуЦө,Ј¬ЛщТФx=7•rҝӮАықҷЧоҙу,ЎЈ
=7•rһйЧоҙуЦө,Ј¬ЛщТФx=7•rҝӮАықҷЧоҙу,ЎЈ
·ЁЛДЈәАыУГҫщЦөІ»өИКҪәН¶Ё·eЧоҙуөДРФЩ|(zhЁ¬)ЗуЧоЦөЈ¬ҝӮАықҷ=(20-x)×(120+20x)=(20-x)×20(6+x),Ј¬Я@•rәт(20-x)+(6+x)=26һй¶ЁЦө,Ј¬®”(dЁЎng)ЗТғH®”(dЁЎng)ЛыӮғПаөИјҙ(20-x)=(6+x)•rіЛ·eЧоҙу,Ј¬ЛщТФx=7•rҝӮАықҷЧоҙу;
Т»о}ЛД·Ё№©ҙујТЯx“сЈ¬ФЪХжХэІҪИлҝјҲцөД•rәтҝЙЯm®”(dЁЎng)Яx“сЧФјәПІҡgІўЯ\(yЁҙn)УГКмҫҡҪв·ЁҪво},Ј¬®”(dЁЎng)И»ҲDНГҪoҙујТҪЁЧhЯҖКЗТФИэ,ЎўЛД·ЁһйЦчЈ¬ҢҰУЪ¶юҙОәҜ”ө(shЁҙ)Кмҫҡ¶ИёЯөДРЎ»п°йТФөЪИэ·ЁһйЦчјҙҝЙҝмЛЩГлҡўо}Дҝ,ЎЈ
ҪУПВҒн,Ј¬ҪoҙујТТ»ӮҖАэо}РЎФҮТ»ПВЕЈө¶Јә
ЎҫАэ2ЎҝДіЖуҳI(yЁЁ)ФO(shЁЁ)УӢБЛТ»ҝо№ӨЛҮЖ·Ј¬ГҝјюөДіЙұҫКЗ70ФӘ,Ј¬һйБЛәПАн¶Ёғr,Ј¬Н¶·ЕКРҲцЯM(jЁ¬n)РРФҮдNЎЈ“ю(jЁҙ)КРҲцХ{(diЁӨo)Ій,Ј¬дNКЫҶОғrКЗ120ФӘ•r,Ј¬ГҝМмөДдNКЫБҝКЗ100јюЈ¬¶шдNКЫҶОғrГҝҪөғr1ФӘ,Ј¬ГҝМмҫНҝЙ¶аКЫіц5јю,Ј¬ө«ТӘЗудNКЫҶОғrІ»өГөНУЪіЙұҫЎЈ„tдNКЫҶОғrһй¶аЙЩФӘ•r,Ј¬ГҝМмөДдNКЫАықҷЧоҙу?
A.100ФӘ
B.102ФӘ
C.105ФӘ
D.108ФӘ
Ўҫҙр°ёЎҝЈәC
ЎҫҪвОцЎҝЈәұҫо}Н¬ҳУРиЗуҪвдNКЫҝӮАықҷЧоҙу,Ј¬ФO(shЁЁ)ГҝҪөөНxФӘЈ¬ГҝМмҫНҝЙТФ¶аЩu5xјюТВ·ю,Ј¬ёщ“ю(jЁҙ)о}ТвҝЙБР·ҪіМдNКЫҝӮАықҷ=(120-x-70)×(100+5x),Бо(120-x-70)×(100+5x)=0ҝЙөГЈәx1=50,Ј¬x2=-20Ј¬®”(dЁЎng)x=![]() =15•rИЎЧоҙуЦө,Ј¬јҙ®”(dЁЎng)120ҪөөН15ФӘһй105ФӘ•r,Ј¬ГҝМмдNКЫАықҷЧоҙуЈ¬ТтҙЛ,Ј¬Яx“сCЯxн—,ЎЈ
=15•rИЎЧоҙуЦө,Ј¬јҙ®”(dЁЎng)120ҪөөН15ФӘһй105ФӘ•r,Ј¬ГҝМмдNКЫАықҷЧоҙуЈ¬ТтҙЛ,Ј¬Яx“сCЯxн—,ЎЈ
”ө(shЁҙ)БҝкP(guЁЎn)Пөо}РНҸН(fЁҙ)лs»ҜЈ¬ПаҢҰҪво}·Ҫ·Ё¶аҳУ»Ҝ,Ј¬ХТөҪЯmәПЧФјәәНҝјҲцөДІЕКЗХжХэөД„ЩАы,Ј¬ДгҢW(xuЁҰ)•юБЛҶб?

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә
ЙПТ»ЖӘЈә2022ДкөДҮшҝјҢW(xuЁҰ)ҶT·ЦПн
ПВТ»ЖӘЈәҝј№«Ҫӣ(jЁ©ng)тһ·ЦПнЦ®ЗуҢW(xuЁҰ)В·ЙПЈ¬В·ВюВюЖдРЮЯh(yuЁЈn)Щв

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc(diЁЈn)“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңК(zhЁіn)ҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ