2021-11-19 14:44:14 ¿¨í(w´Ç)T¢¥åƒW(w´Èng) 
 öáíôÚåÇȤ¡È§´ñøå¤
öáíôÚåÇȤ¡È§´ñøå¤

µ(b´Êo)¢¥Ÿ}§ã£µ,È¢
ë˜W(xu´Î)ÔÇaæèå

å֡ȧ´òÀ¿¨í(w´Ç)T¢¥åçáÅÅy(c´´)¢óá¢øÅȘç(sh´Ç)ê¢õP(gu´Àn)üç¢òúë˜W(xu´Î)?c´´)Öð¢¥Ô^°äøÅñú°Èý£å¡ØãÆ—ç§çáØ£ŸŸ}Åë,ÀÈë˜W(xu´Î)Ø£¯ÐÑ¥òúÂç(sh´Ç)ê¢õP(gu´Àn)üçñéåÖ¢¥åçá柤µØ£(g´´)áÈKëõ°è,ÀÈÔ@Ï(d´Èo)øôêùç(sh´Ç)ê¢õP(gu´Àn)üççáæ—Ÿ}r(sh´ˆ)ÕgOÕ TñÎȘ¤ÉÑÁë˜W(xu´Î)]ÆÅæзçár(sh´ˆ)ÕgÚÔM(j´˜n)ÅÅæ—Ÿ},ȘÔ@æë˜W(xu´Î)üÈë«áÉ·?q´Ý)Wê(x´ˆ)ç§Ø£ñNáÉ·¢šùìæ—°—Ÿ}á¢çáñ§ñ´,ÀÈöاþäšØˆ§oǵ¥Ø§Õ§BçáÝÑç(sh´Ç)ñ´ƒëòúÔ@ÆØ£ñN¢èØ墚ùìûŠÂý¢ñøŸ}Åëçáñ§ñ´ÀÈ
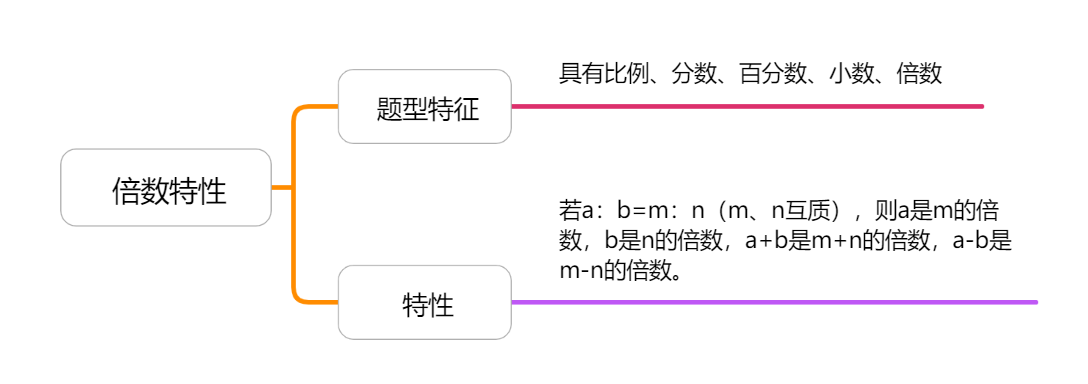
ÝÑç(sh´Ç)ñ´,Șø¡çáòúÛ(d´Àng)Ÿ}á¢øÅ°—˜F(xi´Ên)êùÝàâ»,ÀÂñø?j´¨n)?sh´Ç)À¯ìñø?j´¨n)?sh´Ç),ÀÂÅÀç(sh´Ç)£·ÝÑç(sh´Ç)r(sh´ˆ),ȘÛ(d´Àng)aȤb=mȤn(mÀÂn£Ëì|(zh´˜)),ȘaòúmçáÝÑç(sh´Ç),ȘbòúnçáÝÑç(sh´Ç)Șa+bòúm+nçáÝÑç(sh´Ç),Șa-bòúm-nçáÝÑç(sh´Ç),ÀÈöا(j´ˋng)°Èò¿ÆûÔ@ñNñ§ñ´ûŠÂç(sh´Ç)ê¢õP(gu´Àn)üççáŸ}á¢ÀÈüôûÌöØØ£óÞ(sh´ˆ)Ü`Ø£üô,ÀÈ
Àƒâ»1À¢¥æØØè(g´´)¯Á¡¼ÆÅ30ÑÁû«W(xu´Î)èº,Ș¥æ¯ÁáÅéÛèºÝàÕ5Àû6ȘØدÁáÅéÛèºÝàÕ5Àû4,Ș¥æ,ÀÂØØè¯ÁáÅ躢ç(sh´Ç)ÝàéÛ躢ç(sh´Ç)Ȥ
A.ÑÁ1àùB.èì1àùC.ÑÁ2àùD.èì2àù
Àƒ§ãö—À¢Ÿ}á¢øÅ°—˜F(xi´Ên)êùè(g´´)Ýàâ»õP(gu´Àn)üçȘ¢¥]ò¿ÆûÝÑç(sh´Ç)äÄÅåÔM(j´˜n)ÅŧãŸ},ÀÈ¡ª±(j´Ç)Ÿ}Øã,Ș¥æØØè(g´´)¯ÁçáW(xu´Î)èºàùç(sh´Ç)ƒªåÖ31-39øÛÕgȘû¢(g´´)¯Áçá¢?c´´)ù?sh´Ç)Ñ¥òúáÅèº+éÛèºçáàùç(sh´Ç),ÀÈ¡ª±(j´Ç)ÝÑç(sh´Ç)äÄÅå,Ș¥æ¯Áàùç(sh´Ç)òú5+6=11çáÝÑç(sh´Ç)ȘôðåÖ31-39øÛÕgHÆÅ33,ȘùªØå¥æ¯ÁÆÅ33àù,ȘóðøÅáÅèº15àùȘéÛèº18àù,ÀÈØدÁàùç(sh´Ç)òú5+4=9çáÝÑç(sh´Ç),ȘôðåÖ31-39øÛÕgçáHÆÅ36,ȘùªØåØدÁÆÅ36àùȘóðøÅáÅèº20àù,ȘéÛèº16àù,ÀÈ¥æØØè¯ÁçááÅèºàùç(sh´Ç)Õ15+20=35ȘéÛèºàùç(sh´Ç)Õ18+16=34,ÀÈùªØåáÅèºàùç(sh´Ç)ÝàéÛèºàùç(sh´Ç)ÑÁ1àù,ÀÈ݃Ÿ}ÔxAÀÈ
Àƒâ»2À¢á°øÅW(xu´Î)¡ÔØ£øê¡Ôà»áõ¥(j´ˆ)çáW(xu´Î)èº Â¥Æá°Ú(xi´Êng)èÓ ^(q´Ý)ñ±í(w´Ç),ȘàÓ¿«¡Ôà»áõ¥(j´ˆ)éc¡ÔØ£áõ¥(j´ˆ),À¡Ôà»áõ¥(j´ˆ)éc¡Ôѱáõ¥(j´ˆ) Â¥ÆÇù£ŸÆ(d´¯ng)çáàùç(sh´Ç)øÛÝàñøeÕ5Àû3ÀÂ8Àû5,ȘtåøÅW(xu´Î)¡ÔØ£øê¡Ôà»áõ¥(j´ˆ)æŸèì¿ýÆÅ(ÀÀÀÀ)àù Â¥ÆåÚ(xi´Êng)èÓ ^(q´Ý)ñ±í(w´Ç),ÀÈ
A.40B.55C.79D.89
Àƒ§ãö—À¢ÝƒŸ}øÅ°—˜F(xi´Ên)êùÝàâ»õP(gu´Àn)üçȘ¢¥]ò¿ÆûÝÑç(sh´Ç)äÄÅå§ãŸ},ÀÈâ«Æû¡Ôà»áõ¥(j´ˆ)Âè(g´´)Ýàâ»õP(gu´Àn)üçÔM(j´˜n)ÅÅô(li´Ân)êÂ,Șçû秡ÔأȤ¡ÔѱȤ¡Ôà»=24Ȥ25Ȥ40�,È¢�?c´´)ù?sh´Ç)=¡ÔØ£+¡Ôѱ+¡Ôà»,ȘùªØå¢?c´´)ù?sh´Ç)òú24+25+40=89çáÝÑç(sh´Ç)ÀÈùªØå݃Ÿ}ÔxD,ÀÈ
Àƒâ»3À¢á°îŃ¢èºå¤§þáõçáîÅØ£Åô躿ý1305àùȘÝààËáõå—¥Æêù4.4%,ȘóðøÅéÛèºàùç(sh´Ç)pèì4%,ȘáÅèºàùç(sh´Ç)å—¥Æ10%Ștå大þáõçáîÅØ£ÅôèºøÅÆÅáÅèº()àù,ÀÈ
A.790B.805C.825D.865
Àƒ§ãö—À¢ÝƒŸ}øÅ°—˜F(xi´Ên)êùÝàâ»õP(gu´Àn)üç,Ș¢¥]ò¿ÆûÝÑç(sh´Ç)äÄÅå§ãŸ}ÀÈ¡ª±(j´Ç)áÅèºàùç(sh´Ç)å—¥Æ10%¢èøˆ,Ș§þáõçááÅèºÈ¤àËáõçááÅèº=11Ȥ10,ȘùªØå§þáõçááÅèºòú11çáÝÑç(sh´Ç)ÀÈÆ^ýšÔxÚ(xi´Êng),ȘHCÔxÚ(xi´Êng)òú11çáÝÑç(sh´Ç),ÀÈùªØå݃Ÿ}ÔxCÀÈ
ØåèüƒëòúÝÑç(sh´Ç)äÄÅåçáò¿Æû,ȘåÖàí°Èæ—Ÿ}çáÔ^°äøÅ,Șöر(hu´˜)äÄeõP(gu´Àn)æÂÝàâ»õP(gu´Àn)üççá°—˜F(xi´Ên)ȘàÓ¿«Ÿ}øÅ°—˜F(xi´Ên)Ýàâ»õP(gu´Àn)üç,Șöر(hu´˜)òæüࢥ]ò¿ÆûÝÑç(sh´Ç)äÄÅåÔM(j´˜n)ÅŧãŸ},Șëªëª¢èØåï^¢šçáçû租}á¢çáÇÞ¯¡,ȘëøºÇµ¥Ø¡■¢šçá§ãQç(sh´Ç)ê¢õP(gu´Àn)üçøÅçáý¢ñøŸ}ÅëÀÈý£øˆçâë˜W(xu´Î)W(xu´Î)ê(x´ˆ)çáå¾ûÇÆêùáÄ?

üÁõP(gu´Àn)à(n´´i)àïëóù]Ȥ

ìNÅᢥ¿¨¢ëñ±

ìNÅáÈì¢ëñ±

µ(b´Êo)û«l¥±?
ö£Ôxþ?
¿På¢óá¢?
ûÌåñ§ò§?
......

 åÖƒ¢ëñ±Àê
åÖƒ¢ëñ±Àê

■c(di´Èn)¶ùªÅÒìYêü,ȘÔÇaŸI(l´¨ng)àÀ








íÅ¢¥¿¨¡Ì¢¥åǵƒVôö£ÝÚµ(b´Êo)û«àŠ¢Öò(zh´°n)¢¥æCÇ·ÆÀ¢¥år(sh´ˆ)Õg°è¢(j´ˋ)ýÕåûÌåû«öðÆû¿¨òƒ¢¥å¢šÆ
µ(b´Êo)¢¥ê¼°äµ(b´Êo)¢¥ÇÞµ(b´Êo)¢¥l¥±ôáɧէBí±ýÔñ´Ø(gu´ˋ)µ(b´Êo)¢¥ç(sh´Ç)±(j´Ç)ñøö—váõ¢¥úÕ