2021-11-12 14:49:27 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂí(lšąi)ÔŽŁșșț±±·ÖÔș
ÎÄŐÂí(lšąi)ÔŽŁșșț±±·ÖÔș

ó(bš€o)żŒ(wššn)î}œâ»ó,Łż
ÍŹW(xušŠ)ߎaŚÉÔ

ĐĐłÌ(wššn)î}ÊÇÎÒč«Ő(wšŽ)TżŒÔ”(shšŽ)ÁżêP(gušĄn)Ï”ÄŁKÖĐłŁłöŹF(xiš€n)”ÄÒ»îî}ĐÍ ,ŁŹÄÇÊČĂŽÊÇĐĐłÌ(wššn)î}ÄŰŁżÎÒżÉÒÔß@ÓÈ„Àíœâ Łș ź(dšĄng)î}ÄżÖĐœołöșÍËÙ¶È,ĄąÂ·łÌ,Ąąr(shšȘ)égÏàêP(gušĄn)”ÄlŒțr(shšȘ)ŁŹÎÒżÉÒÔ¶šß@îî}éĐĐłÌ(wššn)î},ĄŁ Š(dušŹ)ÓÚĐĐłÌ(wššn)î},ŁŹ Śî»ù”A(chšł)”Äč«ÊœÊÇŁș·łÌ=ËÙ¶È×r(shšȘ)ég,ŁŹ Š(dušŹ)ÓÚĐĐłÌ(wššn)î}”ÄżŒČì»ù±Ÿ¶ŒÊÇúÀ@Ôč«ÊœŐčé_(kšĄi) ĄŁ ÎÒ°Ń�,ŁżŒ”�ĐĐłÌ(wššn)î}·ÖéÉŽóîŁș»ù±ŸĐĐłÌșÍÏàÓöŚ·Œ°,ĄŁ »ù±ŸĐĐłÌÖśÒȘÊÇ·ÖÎöÖśówÔÚȻ͏ÇéŸłÖĐ”Äß\(yšŽn)Ó(dš°ng)ß^(guš°)łÌ ŁŹÏàÓöŚ·Œ°ÖśÒȘÊÇ·ÖÎöÖśów”ÄÏàŠ(dušŹ)ß\(yšŽn)Ó(dš°ng)ß^(guš°)łÌ,ĄŁ œńÌìÎÒÖŰüc(dišŁn)·ÖÎöÍšß^(guš°)±ÈÀę·šœâQĐĐłÌ(wššn)î},ĄŁ
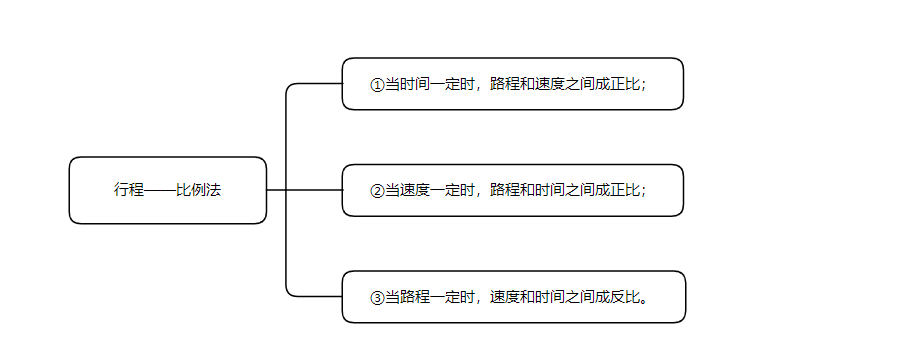
±ÈÀę·šœâQĐĐłÌ(wššn)î}ÊÇÖžź(dšĄng)ËÙ¶ÈĄąÂ·łÌ,Ąąr(shšȘ)égÈę(gšš)ÁżÖĐÆäÖĐÒ»(gšš)ÁżČ»Śr(shšȘ),ŁŹÁíÉ(gšš)ÁżÖźégŽæÔÚÖű·Ž±È»òŐß·Ž±È”ÄêP(gušĄn)Ï”ŁŹÖśÒȘÓĐÈę·NŁș
ąÙ ź(dšĄng)r(shšȘ)égÒ»¶šr(shšȘ),ŁŹÂ·łÌșÍËÙ¶ÈÖźégłÉŐę±È ,Ł»
ąÚź(dšĄng)ËÙ¶ÈÒ»¶šr(shšȘ)ŁŹÂ·łÌșÍr(shšȘ)égÖźégłÉŐę±È,Ł»
ąÛź(dšĄng)·łÌÒ»¶šr(shšȘ),ŁŹËÙ¶ÈșÍr(shšȘ)égÖźégłÉ·Ž±ÈĄŁ
ÄÇÈçșÎÍšß^(guš°)ËûÖźég”ÄêP(gušĄn)Ï”ÍÖúÎÒœâî}ÄŰ,ŁŹœÓÏÂí(lšąi)ÎÒąÍšß^(guš°)Őæî}í(lšąi)W(xušŠ)Á(xšȘ)Ò»ÏÂĄŁ
ĄŸŐæî}1ĄżŒŚ,ĄąÒÒÉÈËÔÚÒ»l 400ĂŚ”Äh(hušąn)ĐÎĆÜ”ÀÉÏÄÏàŸà200ĂŚ”ÄλÖĂłö°l(fšĄ),ŁŹÍŹÏòòËÙĆÜČœĄŁź(dšĄng)ŒŚ”ÚÈęŽÎŚ·ÉÏÒÒ”Är(shšȘ)șò,ŁŹÒÒĆÜÁË2000ĂŚ,ĄŁ(wššn)ŒŚ”ÄËÙ¶ÈÊÇÒҔĶàÉÙ±¶Łż
A. 1.2 B. 1.5
C. 1.6 D. 2.0
ĄŸŽđ°žĄżB
ĄŸœâÎöĄż ”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéĐĐłÌ(wššn)î},ŁŹÙÓÚÏàÓöŚ·Œ°îĄŁ
”Ú¶țČœ,ŁŹh(hušąn)ĐÎÍŹüc(dišŁn)ÍŹÏòłö°l(fšĄ)ĂżŚ·ÉÏÒ»ŽÎ,ŁŹŒŚ±ÈÒÒ¶àĆÜһȊĄŁ”ÚÒ»ŽÎÓÉÓÚÊÇȻ͏Æđüc(dišŁn),ŁŹŒŚ±ÈÒÒ¶àĆÜÔí(lšąi)”ÄČîŸà 200ĂŚ,Ł»ÖźșóÉŽÎŚ·É϶Œ¶àĆÜ400ĂŚŁŹŒŚÒ»čȱÈÒÒ¶àĆÜ200+400×2=1000ŁšĂŚŁ©,ĄŁÒÒĆÜÁË2000ĂŚ,ŁŹŒŚĆÜÁË3000ĂŚŁŹr(shšȘ)égÏàÍŹ,ŁŹtËٶȱÈĆc·łÌ±ÈÒČÏàÍŹ,ŁŹżÉÖȘŒŚ”ÄËÙ¶ÈÊÇÒÒ”Ä3000÷2000=1.5±¶,ĄŁ
ÒòŽËŁŹ±Ÿî}ßxń Bßxí(xiš€ng),ĄŁ
ĄŸŐæî}2Ąż ABÉüc(dišŁn)égÓĐÒ»lÖ±ŸĆÜ”À,ŁŹŒŚÄAüc(dišŁn)łö°l(fšĄ)ŁŹÒÒÄBüc(dišŁn)łö°l(fšĄ),ŁŹÉÈËÍŹr(shšȘ)é_(kšĄi)ÊŒòËÙÔÚÉüc(dišŁn)ÖźégÍù·”ĆÜČœ,ĄŁ”Ú1ŽÎÓĂæÏàÓör(shšȘ)ëxAüc(dišŁn)1000ĂŚŁŹ”ÚÈęŽÎÓĂæÏàÓör(shšȘ)ëxBüc(dišŁn)200ĂŚ,ŁŹŽËr(shšȘ)ŒŚ”œß_(dšą)Büc(dišŁn)2ŽÎ,ŁŹÒÒ”œß_(dšą)Aüc(dišŁn)1ŽÎŁŹ(wššn)ABÉüc(dišŁn)égĆÜ”À”ÄéL(zhšŁng)¶ÈÊǶàÉÙĂŚ?
A.1400 B.1500
C. 1600 D.1700
ĄŸŽđ°žĄżC
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéĐĐłÌ(wššn)î},ŁŹÓñÈÀę·šœâî}ĄŁ
”Ú¶țČœ,ŁŹ”ÚÒ»ŽÎÓĂæÏàÓöÉÈËčČŚß 1(gšš)È«łÌ,ŁŹ”ÚÈęŽÎÓĂæÏàÓöÉÈËčČŚß5(gšš)È«łÌŁŹÄÇĂŽÉŽÎÏàÓöŒŚŚßß^(guš°)”Ä·łÌÖź±Èé1ĄĂ5,ĄŁÔO(shšš)È«łÌésĂŚ,ŁŹŒŚ”œß_(dšą)Büc(dišŁn)2ŽÎŁŹtŒŚ”ÚÈęŽÎÏàÓör(shšȘ)Ćܔğàëxé3S+200ĂŚ,ŁŹÓĐ1000ĄĂŁš3s+200Ł©=1ĄĂ5,ŁŹœâ”Ăs=1600ĄŁ
ÒòŽË,ŁŹßxń Cßxí(xiš€ng),ĄŁ
ĄŸŐæî}3ĄżĐĄé_(kšĄi)Üœ(jš©ng)žßËÙč«Â·ÄŒŚ”ŰÇ°ÍùÒÒ”ŰĄŁÔžßËÙč«Â·ÏȚËÙé 120ǧÌ/ĐĄr(shšȘ),ĄŁ·”łÌr(shšȘ)°l(fšĄ)ŹF(xiš€n)ÓĐ1/3”Ä·¶ÎŐęÔÚŸSĐȚ,ŁŹÇÒŸSĐȚ·¶ÎÏȚËÙœ”é60ǧÌ/ĐĄr(shšȘ)ĄŁÒŃÖȘĐĄÈ«łÌŸù°ŽŚîžßÏȚËÙĐĐń,ŁŹÇÒ·”łÌÓĂr(shšȘ)±ÈÈ„łÌÓĂr(shšȘ)¶à30·Öç,ŁŹtŒŚĄąÒÒÉ”ŰŸàëxé¶àÉÙǧÌ,Łż
A.150 B.160
C.180 D.200
ĄŸŽđ°žĄż C
ĄŸœâÎöĄż”ÚÒ»Čœ,ŁŹ±Ÿî}żŒČéĐĐłÌ(wššn)î}ŁŹÓñÈÀę·šœâî},ĄŁ
”Ú¶țČœ,ŁŹ 120ǧÌ/ĐĄr(shšȘ)Ćc60ǧÌ/ĐĄr(shšȘ)ŁŹËÙ¶ÈÖź±Èé2ĄĂ1,ŁŹËÙ¶ÈĆcr(shšȘ)égłÉ·Ž±È,ŁŹËùĐèr(shšȘ)égÖź±Èé1ĄĂ2,ŁŹ·”łÌ±ÈÈ„łÌÓĂr(shšȘ)¶à30·Ö磏żÉÖȘ1·Ęr(shšȘ)égé30·ÖçŁšÈ„łÌ30·Öç,Ąą·”łÌ60·Ö磩,ŁŹÈ«łÌ”Ä È„łÌÓĂr(shšȘ)30·ÖçŁœ0.5ĐĄr(shšȘ)ŁŹŒŚ,ĄąÒÒÉ”ŰŸàëxé120×0.5×3Łœ180ŁšÇ§ĂŚŁ©,ĄŁ
ÒòŽËŁŹßxń Cßxí(xiš€ng),ĄŁ
Íšß^(guš°)ÒÔÉÏ”Äî}ÄżżÉÒÔżŽłö,ŁŹß\(yšŽn)ÓñÈÀę·šœâĐĐłÌ(wššn)î}Č»HżÉÒÔÍÎÒ”Ă”œŐęŽ_Žđ°žŁŹßÄÜÌážßÎÒ”ÄŚöî}ËÙ¶È,ĄŁÒòŽË,ŁŹÎÒÒȘÊìÓ±ÈÀę·š”ÄÖȘŚR(shšȘ)üc(dišŁn)ŁŹÇÉÓñÈÀę·šœâQĐĐłÌ(wššn)î},ĄŁ
ĄŸ ËŒŸS§(dšŁo)D Ąż

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț
ÉÏÒ»ÆȘŁșĐĐy(cšš)”(shšŽ)ÙYäżŒžÉŰÖźÇÉœâ»ùÆÚșÍČîÊĄr(shšȘ)ég
ÏÂÒ»ÆȘŁș2022ÊĄÂ(lišąn)żŒĐĐy(cšš)”(shšŽ)ÁżêP(gušĄn)Ï”ÖźÇÉÓĂŽúÈëĆĆłę·š

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏ,ŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉż(jš©)ČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒ(wššn)Žđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé
”(shšŽ)ÁżêP(gušĄn)Ï”ŃÔŐZ(yšł)ÀíœâĆĐàÍÆÀíÙYÁÏ·ÖÎöłŁŚR(shšȘ)ĆĐàĐĐy(cšš)ŒŒÇÉ