2021-09-22 17:13:29 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂí(lšąi)ÔŽŁșÉÏșŁ·ÖÔș
ÎÄŐÂí(lšąi)ÔŽŁșÉÏșŁ·ÖÔș

ó(bš€o)żŒ(wššn)î}œâ»óŁż
ÍŹW(xušŠ)ߎaŚÉÔ

ÔÚĐĐy(cšš)żŒÔź(dšĄng)ÖĐŁŹĆĆÁĐœMșÏÒÔŒ°žĆÂÊÊÇżŒČéîlŽÎĘ^žß”ÄÒ»(gšš)ÖȘŚR(shšȘ)üc(dišŁn)ŁŹœâQß@Ò»î(wššn)î}ÓĐÒ»·N·œ·šœĐŚööĆe·š,ŁŹœÓÏÂí(lšąi)ÎÒŸÍí(lšąi)Ő?wšŽ)ß@·N·œ·šĄŁ
öĆe·š
Ò»°ăŠ(dušŹ)ÓÚî}ÄżÖĐ”(shšŽ)ț(jšŽ)Ę^ĐĄ,ĄąÇérÓÖČ»ÊÇșܶà,ŁŹ»òŐßÓĂĆĆÁĐœMșÏČ»ŽóșñíÊŸ”Är(shšȘ)șòŁŹŽËr(shšȘ)żÉÒÔLÔÓĂÒ»ÏÂöĆe·š,ĄŁ”«ÓĐĐ©ÈËÔÚÊčÓĂöĆe·š”Är(shšȘ)șò,ŁŹț(hušŹ)ąÒ»Đ©Çér©”ôŁŹ»òŐß°ŃÒ»Đ©ÇérÈĄÖŰÍ(fšŽ),ĄŁÖźËùÒÔłöŹF(xiš€n)ß@îÇér,ŁŹÖśÒȘÎÒ?cšš)ÚöĆe”Är(shšȘ)șòŁŹÄXŚÓź(dšĄng)ÖĐÊÇÏ딜һ·NÇérŸÍһϷNÇér,ŁŹ±ÈĘ^Áèy,ĄŁ”«ÈçčûÄXŚÓź(dšĄng)ÖĐÓĐÒ»¶š”ÄßĘŁŹ°ŽŐŐß@(gšš)ßĘÍùÏ”ÄÔ,ŁŹŸÍț(hušŹ)±ÜĂâß@·NÇérłöŹF(xiš€n)ĄŁ
Àęî}Ÿ«Öv
ĄŸÀę1ĄżÄłÊĐÙ|(zhšŹ)zČżéTŠ(dušŹ)ÊĐĂæÉÏłŁÒ(jiš€n)”ÄÊÖłÖÊœówŰßM(jšŹn)ĐĐÙ|(zhšŹ)ÁżłéČé,ŁŹą10(gšš)Č»ÍŹÆ·ĆÆ”ÄówŰ·ÖeßM(jšŹn)ĐĐŸÌ(hš€o)(1Ì(hš€o)”œ10Ì(hš€o)),ŁŹÈ»șóëSC(jš©)łéÈĄÁË3(gšš)ŸÌ(hš€o)ßM(jšŹn)ĐĐzČ飏tßxńówŰ”Ä3(gšš)ŸÌ(hš€o)ŐęșĂßBÌ(hš€o)”ÄžĆÂÊé(ĄĄĄĄ),ĄŁ

ĄŸŽđ°žĄżC
ĄŸœâÎöĄż±Ÿî}żŒČéžĆÂÊ,ŁŹžĆÂÊ=MŚălŒțÇér”(shšŽ)/ż”ÄÇér”(shšŽ)ŁŹ±Ÿî}żÇér”(shšŽ)șĂÇó,ŁŹżÇér”(shšŽ)é![]() ,ŁŹ”«ÊÇ3(gšš)ŸÌ(hš€o)ŐęșĂßBÌ(hš€o)”ÄÇér”(shšŽ)ÓĂĆĆÁĐœMșÏČ»ŽóșñíÊŸŁŹÔÙt±Ÿî}”(shšŽ)ț(jšŽ)Ę^ĐĄŸÌ(hš€o)ż”(shšŽ)Ö»ÓĐ10,ŁŹËùÒÔÏ딜ÓĂöĆe·š°ŃËùÓĐMŚălŒț”ÄÇér”(shšŽ)±íÊŸłöí(lšąi),ŁŹ(1ŁŹ2,ŁŹ3)(2,ŁŹ3ŁŹ4)(3,ŁŹ4,ŁŹ5)(4ŁŹ5,ŁŹ6)(5,ŁŹ6,ŁŹ7)(6ŁŹ7,ŁŹ8)(7,ŁŹ8ŁŹ9)(8,ŁŹ9,ŁŹ10)ŁŹčČ8ÖĐÇér,ŁŹžùț(jšŽ)žĆÂÊč«Êœ,ŁŹČąŽúÈë”(shšŽ)ț(jšŽ)”ĂžĆÂÊ
,ŁŹ”«ÊÇ3(gšš)ŸÌ(hš€o)ŐęșĂßBÌ(hš€o)”ÄÇér”(shšŽ)ÓĂĆĆÁĐœMșÏČ»ŽóșñíÊŸŁŹÔÙt±Ÿî}”(shšŽ)ț(jšŽ)Ę^ĐĄŸÌ(hš€o)ż”(shšŽ)Ö»ÓĐ10,ŁŹËùÒÔÏ딜ÓĂöĆe·š°ŃËùÓĐMŚălŒț”ÄÇér”(shšŽ)±íÊŸłöí(lšąi),ŁŹ(1ŁŹ2,ŁŹ3)(2,ŁŹ3ŁŹ4)(3,ŁŹ4,ŁŹ5)(4ŁŹ5,ŁŹ6)(5,ŁŹ6,ŁŹ7)(6ŁŹ7,ŁŹ8)(7,ŁŹ8ŁŹ9)(8,ŁŹ9,ŁŹ10)ŁŹčČ8ÖĐÇér,ŁŹžùț(jšŽ)žĆÂÊč«Êœ,ŁŹČąŽúÈë”(shšŽ)ț(jšŽ)”ĂžĆÂÊ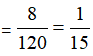 ŁŹÒòŽË,ŁŹ±Ÿî}Žđ°žßxńC,ĄŁ
ŁŹÒòŽË,ŁŹ±Ÿî}Žđ°žßxńC,ĄŁ
ĄŸÀę2ĄżÄłÈËÉÏÇÌĘŁŹĂżÒ»ČœżÉÒÔżç1(gšš)Ć_(tšąi)ëA»ò2(gšš)Ć_(tšąi)ëA»ò3(gšš)Ć_(tšąi)ëA,ŁŹtÉÏ”œ”Ú5(gšš)Ć_(tšąi)ëA,ŁŹÓĐ( )·N·œ·š
AĄą3 B,Ąą6
C,Ąą8 DĄą13
ĄŸŽđ°žĄżD
ĄŸœâÎöĄż±Ÿî}żŒČéĆĆÁĐœMșÏ,ŁŹŚxÍêî}șó°l(fšĄ)ŹF(xiš€n),ŁŹ±Ÿî}żŽËÆș(jišŁn)ÎŁŹ”«ÓĂĆĆÁĐœMșÏȹȻșñíÊŸ,ŁŹ»òŐßÓĂĆĆÁĐœMșÏȹȻÊÇżÉÒÔșÜșĂ”ÄÖ±œÓ±íÊŸłöí(lšąi),ŁŹÔÙt±Ÿî}”(shšŽ)ț(jšŽ)ÒȱÈĘ^ĐĄŁŹÖ»ÓĐ5(gšš)Ć_(tšąi)ëA,ŁŹżÉÒÔÓĂöĆe·šąÆäÇérÒ»Ò»ÁĐĆełöí(lšąi),ĄŁÁĐĆe”Är(shšȘ)șòÒȘÓĐÒ»¶š”ÄßĘŁŹ±Ÿî}ĂżÒ»ČœżÉÒÔżç1(gšš)Ć_(tšąi)ëA»ò2(gšš)Ć_(tšąi)ëA»ò3(gšš)Ć_(tšąi)ëA,ŁŹÊŚÏÈżÉÒÔ·ÖÉŽóîÇérŁș1,ĄąÓĐÒ»Čœżç3(gšš)Ć_(tšąi)ëA;2Ąą](mšŠi)ÓĐÒ»Čœżç3(gšš)Ć_(tšąi)ëA;”ÚÒ»îÇér,ĄąÓĐÒ»Čœżç3(gšš)Ć_(tšąi)ëA,ŁŹżÉÒÔÓĐ(3Ąą2),ŁŹ(3,Ąą1Ąą1),ŁŹÆäÖĐ,ŁŹ(3,Ąą2)ÓĐ2·NżÉÄÜŁŹ(3,Ąą1,Ąą1)ÓĐ3·NżÉÄÜŁŹËùÒÔ”ÚÒ»îÇérčČ5ÖĐżÉÄÜ;”Ú¶țîÇér,Ąą](mšŠi)ÓĐÒ»Čœżç3(gšš)Ć_(tšąi)ëA”ÄÇér,ŁŹÓÖżÉÀ^Àm(xšŽ)·ÖÓĐÒ»Čœ2(gšš)Ć_(tšąi)ëAÇér”ÄÇérŁŹżÉÒÔÊÇ(2,Ąą2,Ąą1)ŁŹ(2,Ąą1,Ąą1Ąą1),ŁŹÆäÖĐ(2,Ąą2Ąą1)ÓĐ3·NżÉÄÜ,ŁŹ(2,Ąą1Ąą1,Ąą1)ÓĐ4·NżÉÄÜ;ÁíÒ»î](mšŠi)ÓĐÒ»Čœżç2(gšš)Ć_(tšąi)ëA”Ä(1,Ąą1Ąą1,Ąą1Ąą1),ŁŹÖ»ÓĐ1·NżÉÄÜ,ŁŹËùÒÔ”Ú¶țîÇérčČÓĐ8·NżÉÄÜĄŁčÊżčČÓĐ5+8=13ÖĐżÉÄÜ,ĄŁÒòŽË,ŁŹßxńDĄŁ
öĆe·šÓĐr(shšȘ)șòČ»”«żÉÒÔÓĂÔÚĆĆÁĐœMșÏ(wššn)î}ÉÏ,ŁŹÆäËû(wššn)î},ŁŹÈçÈŐÆÚ(wššn)î}ĄąÖ”ÈŐ(wššn)î}”ÈÓĐr(shšȘ)șòÒČżÉÒÔÓĂöĆe·š,�,ŁżÖźÔÚÊčÓĂöĆe·š”Är(shšȘ)șòŁŹé±ÜĂâ°ŃÒ»Đ©ÇérÈĄÂ©»òŐßŐf(shuš)ÈĄÖŰ,ŁŹÔÚ·ÖÎöÇér”Är(shšȘ)șò,ŁŹÒ»¶šÒȘ°ŽÒ»¶š”ÄßĘßM(jšŹn)ĐĐöĆe,ĄŁ

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț
ÉÏÒ»ÆȘŁșÉÏșŁÊĐżŒĐĐy(cšš)ŒŒÇÉŁșĐĐŐț·šäżŒÖźĄ°ÈęČœŚßĄ±
ÏÂÒ»ÆȘŁș2022Äêű(gušź)żŒĐĐy(cšš)ŚîĐÂĐĐŐțÌÁP·šżŒüc(dišŁn)îA(yšŽ)y(cšš)

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉż(jš©)ČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒ(wššn)Žđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé
”(shšŽ)ÁżêP(gušĄn)Ï”ŃÔŐZ(yšł)ÀíœâĆĐàÍÆÀíÙYÁÏ·ÖÎöłŁŚR(shšȘ)ĆĐàĐĐy(cšš)ŒŒÇÉ