2021-07-23 09:01:04 đŦÕ(wĻī)TŋžÔūW(wĻĢng) 
 ÎÄÕÂí(lĻĒi)ÔīĢšČAD―ĖÓý
ÎÄÕÂí(lĻĒi)ÔīĢšČAD―ĖÓý
Ąū§(dĻĢo)ŨxĄŋąūî}ÓÉđŦÕ(wĻī)TŋžÔūW(wĻĢng)ĖáđĐÔî}ŲYÁÏĢŽÔî}Č(nĻĻi)ČÝí(lĻĒi)Ôī2021Äę0327šÓąąđŦÕ(wĻī)TŋžÔĄķÐÐy(cĻĻ)Ą·Õæî}ĢĻūW(wĻĢng)ÓŅŧØĢĐÖÐĩÄÐÐy(cĻĻ)ÔūíÖÐĩÄĩÚČýēŋ·Ö ĩ(shĻī)ÁŋęP(guĻĄn)Ïĩ,ĢŽŌÔÏÂéÔî}Ôž(xĻŽ)ÐÅÏĒž°―âÎöĢŽÐčŌŠÔî}ŲYÁÏĩÄÐĄŧï°éŋÉŌÔĖížÓČAD―ĖÓýđŲ·―đŦąĖ(hĻĪo)huatuvŦ@ČĄÔî}ŲYÁÏ,ĄĢ
ĄūÔî}ĄŋÄģĘÐ―IÓÐŌŧĖß
éL(zhĻĢng)é50ÃŨĩÄĩČß
Čý―ĮÐÎVö(chĻĢng),ĄĢVö(chĻĢng)ĀïÔO(shĻĻ)Ó(jĻŽ)ÓÐČý(gĻĻ)īóÐĄÏāĩČĩÄAh(huĻĒn)ųZÂŅĘŊĩĀ·đĐĘÐÃņÉĒē―ĢŽČįDËųĘū,ĢŽļũAÏāĮÐ,ĢŽļũAÅcČý―ĮÐÎŌēÏāĮÐĢŽ(wĻĻn)ŅØČý(gĻĻ)Ah(huĻĒn)ÍâúĘŊĩĀĢĻēŧšŽAĮÐüc(diĻĢn)ÖŪégĩÄ�,ĄĢĐÉĒē―ŌŧČĶžséķāÉŲÃŨ,Ģŋ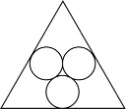
A.95
B.105
C.115
D.125
Ąū―âÎöĄŋ―â·ĻŌŧĢšĩÚŌŧē―ĢŽąūî}ŋžēéŨšÎÓ(jĻŽ)Ëã,ĄĢ
ĩÚķþē―,ĢŽČįÏÂDĄĢ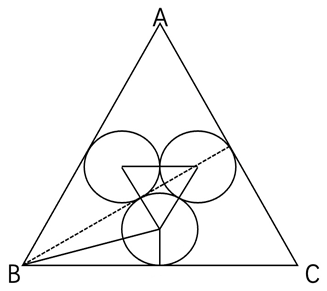
ßB―ÓČý(gĻĻ)Č(nĻĻi)ĮÐAĩÄAÐÄ,ĢŽŋÉÖŠéĩČß
Čý―ĮÐÎ,ĢŽČý(gĻĻ)AÖŪégĩÄŧĄÐÄ―Įķžé60ĄãĢŽŋÉÖŠČý(gĻĻ)AÖŪégĩÄŧĄéL(zhĻĢng)ļũŨÔÕžČý(gĻĻ)ÐĄAÖÜéL(zhĻĢng)ĩÄ,ĢŽĘĢÓāēŋ·ÖÕžČý(gĻĻ)ÐĄAÖÜéL(zhĻĢng)ĩÄ
,ĢŽļųþ(jĻī)AÖÜéL(zhĻĢng)đŦĘ―2ĶÐrĢŽtČý(gĻĻ)AÍâŧĄéL(zhĻĢng)ĘŊĩĀé2ĶÐrĄÁ
ĄÁ3=5ĶÐrĢŽĮóģöÐĄA°ë―žīŋÉ,ĄĢ
ĩÚČýē―,ĢŽČįÏÂDËųĘūĄĢ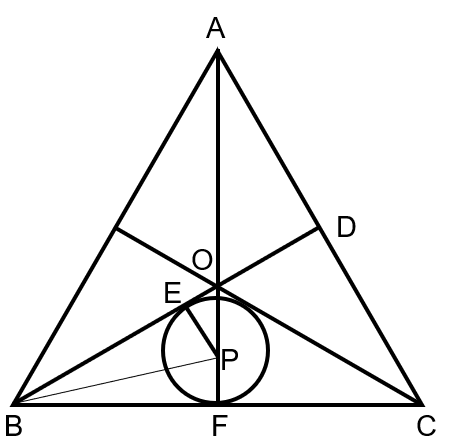
ŨöģöĩČß
Čý―ĮÐÎĩÄČýl―ĮÆ―·Öū,ĢŽ―ŧÓÚŌŧüc(diĻĢn)O,ĄĢļųþ(jĻī)ĩČß
Čý―ĮÐÎĩÄÐÔŲ|(zhĻŽ)ŋÉÖŠĄÏEOP=60ĄãĢŧÐĄAAÐÄPŌýīđū―ŧBDÓÚE,ĢŽÓÉÓÚÏāĮÐŋÉÖŠČý―ĮÐÎEOPĘĮÖą―ĮČý―ĮÐÎ,ĢŽtÐĄA°ë―EP=r=OEĄĢÓÖŌōBE=BF=25=
BO,ĢŽŋÉÖŠBO=
,ĢŽtOE=BO-BE=
Ģ25ĢŽŋÉÖŠr=50Ģ25
ĄÖ25ĄÁĢĻ2Ģ1.732ĢĐ=6.7,ĄĢtČý(gĻĻ)AÍâŧĄéL(zhĻĢng)ĘŊĩĀé5ĶÐrĄÖ105.19,ĄĢ
ŌōīËĢŽßxņBßxí(xiĻĪng),ĄĢ
―â·ĻķþĢšĩÚŌŧē―,ĢŽąūî}ŋžēéŨšÎÓ(jĻŽ)ËãĄĢ
ĩÚķþē―,ĢŽßB―ÓČý(gĻĻ)Č(nĻĻi)ĮÐAĩÄAÐÄ,ĢŽŋÉÖŠéĩČß
Čý―ĮÐÎĢŽČý(gĻĻ)AÖŪégĩÄŧĄÐÄ―Įķžé60Ąã,ĢŽŋÉÖŠČý(gĻĻ)AÖŪégĩÄŧĄéL(zhĻĢng)ļũŨÔÕžČý(gĻĻ)ÐĄAÖÜéL(zhĻĢng)ĩÄ,ĢŽĘĢÓāēŋ·ÖÕžČý(gĻĻ)ÐĄAÖÜéL(zhĻĢng)ĩÄ
ĢŽtČý(gĻĻ)AÍâŧĄéL(zhĻĢng)ĘŊĩĀé2ĶÐrĄÁ
ĄÁ3=5ĶÐr,ĢŽĮóģöÐĄA°ë―žīŋÉ,ĄĢ
ĩÚČýē―ĢŽČįDËųĘū,ĄĢ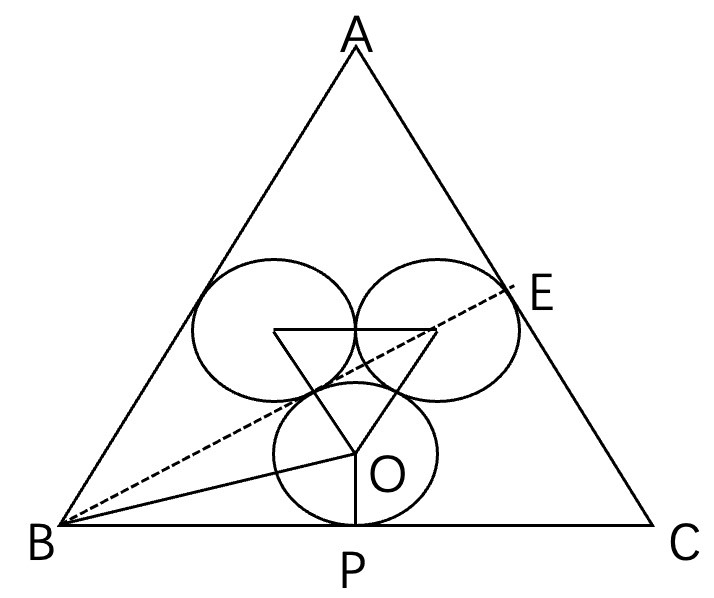
ŨöÝoÖúūBEīđÖąAC,ĢŽtĄÏEBC=30ĄãĢŽÐĄAAÐÄOŌýīđū―ŧBCÓÚP,ßB―ÓOB,ĢŽtÆ―·ÖĄÏEBC,ĢŽŋÉĩÃĢŽĄÏOBC=15Ąã,ĢŽļųþ(jĻī)tan15Ąã=ĄÖ0.268,ĢŽBP=25ĢŽŋÉĩÃOP=6.7,ĢŽtČý(gĻĻ)AÍâŧĄéL(zhĻĢng)ĘŊĩĀé5ĶÐrĄÖ5ĄÁ3.14ĄÁ6.7=105.19,ĄĢ
ŌōīËĢŽßxņBßxí(xiĻĪng)ĄĢ
ÐĄŲNĘŋĢšČįšÎĮó―âtan15Ąã,ĄĢtanĢĻĶÁĢĶÂĢĐ=,ĢŽttan15Ąã=tanĢĻ60ĄãĢ45ĄãĢĐ=
ĢŽtan60Ąã=
,ĢŽtan45Ąã=1,ĢŽŋÉĩÃtan15Ąã=
ĄÖ2Ģ1.732=0.268ĄĢ

ÏāęP(guĻĄn)Č(nĻĻi)ČÝÍÆË]Ģš
ÉÏŌŧÆŠĢšđŦÕ(wĻī)TÄĢMî}―âÎöīð°ļÄģŅbÐÞđŦËūÓŲ(gĻ°u)ÁËŌŧléL(zhĻĢng)é2.5mĩÄlÐÎēŧäPäđÜ,ĢŽŌŠžôēÃ
ÏÂŌŧÆŠĢšĘĄŋžŋžÔvÄęÄĢMî}É(gĻĻ)īóČ˧ËÄ(gĻĻ)šĒŨÓČĨŨøÖŧÓÐÁų(gĻĻ)ÎŧÖÃĩÄAÐÍÐýÞD(zhuĻĢn)ÄūņR,ĢŽ

ó(bĻĪo)Ãûlžþ?
Îŧßxņ?
đPÔŋÆÄŋ?
ÃæÔ·―Ę―?
......

 ÔÚūŋÍ·þĄÁ
ÔÚūŋÍ·þĄÁ

üc(diĻĢn)ôËųÐčŲYÁÏ,ĢŽßīaîI(lĻŦng)ČĄ








ÕÐŋžđŦļæŋžÔīóūVÂÎŧąíó(bĻĪo)ÃûČëŋÚĘ(zhĻģn)ŋžŨCīōÓĄŋžÔr(shĻŠ)égģÉŋ(jĻĐ)ēéÔÃæÔÃûÎäÓÃđŦĘūŋžÔŋėÓ
ó(bĻĪo)ŋžÁũģĖó(bĻĪo)ŋž(wĻĻn)īðó(bĻĪo)ŋžlžþÂÄÜ―é―BÕþēß·ĻŌ(guĻĐ)ó(bĻĪo)ŋžĩ(shĻī)þ(jĻī)·ÖÎövÄęŋžĮé
ĩ(shĻī)ÁŋęP(guĻĄn)ÏĩŅÔÕZ(yĻģ)Āí―âÅÐāÍÆĀíŲYÁÏ·ÖÎöģĢŨR(shĻŠ)ÅÐāÐÐy(cĻĻ)žžĮÉ