2021-05-31 16:32:27 ╣½äš(w©┤)åT┐╝įćŠW(w©Żng) 
 ╬─š┬üĒį┤Ż║╔Ž║ŻĘųį║
╬─š┬üĒį┤Ż║╔Ž║ŻĘųį║

ł¾┐╝å¢Ņ}ĮŌ╗¾,Ż┐
═¼īW(xu©”)Æ▀┤aū╔įā

į┌ąą£y┐Ų─┐┐╝įćųąŻ¼īW(xu©”)åT╣½šJ(r©©n)Ą─ĖąėXūŅ“ūŅŅ^╠█” Ą──ŻēKŠ═╩ŪöĄ(sh©┤)┴┐ĻP(gu©Īn)ŽĄ,ĪŻŲõīŹ,Ż¼ų╗꬚Ų╬šöĄ(sh©┤)┴┐ĻP(gu©Īn)ŽĄŅ}─┐Ą─ĮŌŅ}╝╝Ū╔║═ĘĮĘ©,Ż¼å¢Ņ}Š═Ģ■ėŁ╚ąČ°ĮŌĪŻĮ±╠ņ,Ż¼ąĪŠÄŠ═Įo┤¾╝ęĘųŽĒ╚ń║╬ŲŲĮŌ┐šķgÄū║╬å¢Ņ}—«ŗłDśŗ(g©░u)įņ,Ż¼ŽŻ═¹─▄Įo┤¾╝ę?gu©®)¦üĒę╗ą®åó░l(f©Ī)ĪŻ
ę╗,Īó┐šķgÄū║╬śŗ(g©░u)įņ
Äū║╬śŗ(g©░u)įņŻ║┐╝▓ķī”ė┌┐═ė^╩┬╬’Ą─┐šķgą╬╩Į▀M(j©¼n)ąąĘų╬÷,ĪóšJ(r©©n)ų¬Ą─╦╝ŠS─▄┴”Ż¼ąĶę¬ĮY(ji©”)║ŽŽÓĻP(gu©Īn)Äū║╬╣½╩ĮįŁ└ĒüĒĮŌøQå¢Ņ},ĪŻĮŌøQ▀@ŅÉå¢Ņ}Ą─ĻP(gu©Īn)µI╩ŪŻ║ę¬░č│ķŽ¾Ą─Äū║╬╦╝ŠS,Ż¼ė├«ŗłDĄ─ą╬╩Įą╬Ž¾Ą─▒Ē¼F(xi©żn)│÷üĒŻ¼╚╗║¾▌oų·ėŗ╦Ń,ĪŻ
Č■,Īó└²Ņ}Š½ųv
ūą╝Ü(x©¼)ķåūxŅ}Ė╔Ż¼Ė∙ō■(j©┤)Ņ}ęŌ,Ż¼«ŗłDš╣¼F(xi©żn)Ņ}─┐ųą╩┬╬’Ą─╬╗ų├ĻP(gu©Īn)ŽĄ,Ż¼╚╗║¾╠ūė├Äū║╬╣½╩ĮüĒĮŌŅ}ĪŻ
ĪŠ└²1Ī┐ę╗ų▒╔²ÖCį┌║Ż╔ŽŠ╚į«ąąäėųą╦č╦„ĄĮė÷ļUš▀ĘĮ╬╗║¾═©ų¬┐ņ═¦,Ż¼┐ņ═¦┴ó╝┤│»ė÷ļUš▀ų▒ŠĆ±é?c©©)�,ĪŻ┤╦ĢrŻ¼ų▒╔²ÖCŠÓļx║ŻŲĮ├µĄ─┤╣ų▒Ė▀Č╚200├ū,Ż¼Å─ÖC╔Ž┐┤,Ż¼ė÷ļUš▀į┌š²─ŽĘĮŽ“Ż¼Ė®ĮŪ(│»Ž┬┐┤ĢręĢŠĆ┼c╦«ŲĮ├µĄ─ŖAĮŪ)×ķ30°,Ż¼┐ņ═¦į┌š²¢|ĘĮŽ“,Ż¼Ė®ĮŪ×ķ45°ĪŻ╚¶║÷┬į«ö(d©Īng)Ģr’L(f©źng)Ž“,Īó│▒┴„Ą╚Ųõ╦³ę“╦ž,Ż¼Ūę╝┘Č©ė÷ļUš▀╬╗ų├▓╗ūāŻ¼ät┐ņ═¦ęį60Ū¦├ū/ąĪĢrĄ─╦┘Č╚ä“╦┘Ū░▀M(j©¼n)ąĶę¬ČÓķLĢrķg▓┼─▄ĄĮ▀_(d©ó)ė÷ļUš▀Ą─╬╗ų├? ( )
A,Īó21├ļ BĪó22├ļ
C,Īó23├ļ D,Īó24├ļ
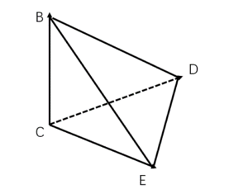
ĪŠĮŌ╬÷Ī┐DĪŻĄ┌ę╗▓Į,Ż¼▒ŠŅ}┐╝▓ķÄū║╬å¢Ņ},Ż¼ī┘ė┌┴ó¾wÄū║╬ŅÉĪŻĄ┌Č■▓Į,Ż¼Ė∙ō■(j©┤)Ņ}ęŌ,Ż¼ū÷│÷╚ńŽ┬┴ó¾włD(ęŖłD1),Ż¼ätBC=200├ūŻ¼∠BEC=30°,Ż¼∠BDC=45°,Ż¼∠DCE=90°Ż¼∠BCD=90°,Ż¼∠BCE=90°,Ż¼Č°1├ū/├ļ=3.6Ū¦├ū/ąĪĢrŻ¼į┌ų▒ĮŪ╚²ĮŪą╬BCEųą,Ż¼,Ż¼CE=200
(├ū)ĪŻį┌ų▒ĮŪ╚²ĮŪą╬BCDųą,Ż¼DC=BC=200(├ū),ĪŻį┌ų▒ĮŪ╚²ĮŪą╬DCEųąŻ¼DE=
(├ū),ĪŻĄ┌╚²▓Į,Ż¼ät╦∙ė├Ģrķg×ķ:400÷
=24(├ļ)ĪŻę“┤╦,Ż¼▀xō±D▀xĒŚ,ĪŻ
ĪŠ└²2Ī┐ę╗╬╗īW(xu©”)╔·į┌ŠÓļx¤ßÜŌŪ“100├ū╠Äė^┐┤╦³Ų’wĪŻį┌¤ßÜŌŪ“Ų’w║¾,Ż¼īW(xu©”)╔·ūóęŌĄĮ¤ßÜŌŪ“Ēö▓┐Å─╦¹Ą─č÷ĮŪ30°╔Ž╔²ĄĮ45°,Ż¼į┘Å─45°╔Ž╔²ĄĮ60°Ą─╬╗ų├Ęųäeė├┴╦11├ļ║═17├ļĪŻätŪ░║¾ā╔Č╬Ģrķg¤ßÜŌŪ“ŲĮŠ∙╔Ž╔²╦┘Č╚Ą─▒╚ųĄ╝s×ķ( )
A,Īó0.89 B,Īó0.91
CĪó1.12 D,Īó1.10
ĪŠĮŌ╬÷Ī┐A,ĪŻĄ┌ę╗▓ĮŻ¼▒ŠŅ}┐╝▓ķÄū║╬å¢Ņ},Ż¼ī┘ė┌ŲĮ├µÄū║╬ŅÉ,ĪŻĄ┌Č■▓ĮŻ¼╚ńŽ┬łD╦∙╩Š(łD2),Ż¼ė╔Ņ}ęŌ┐╔ų¬OAŠÓļx×ķ100├ū,Ż¼∠AOB=30°Ż¼∠AOC=45°,Ż¼∠AOD=60°,Ż¼┐╔Ą├AB=Ż¼AC=100,Ż¼AD=100
,Ż¼ätā╔┤╬╔Ž╔²Ą─ŠÓļx×ķBC=AC-AB=100-
≈42.26,Ż¼CD=AD-AC=100-100≈73.2,Ė∙ō■(j©┤)¤ßÜŌŪ“BĄĮC╦∙ė├Ģrķgt1=11s,CĄĮD╦∙ė├Ģrķgt2=17s,┐╔Ą├v1=
≈3.84Ż¼4.31,╣╩v2=
≈0.89,ĪŻę“┤╦,Ż¼▀xō±A▀xĒŚĪŻ

łD2
ĪŠ└²3Ī┐▄Ŗ╩┬č▌┴Ģ(x©¬)Ą──ŻöMæ(zh©żn)ł÷╔Žėą3éĆę¬³c,Ż¼B³cį┌A³cš²▒▒ĘĮ3Ū¦├ū╠Ä,Ż¼C³cį┌A³cš²¢|ĘĮ4Ū¦├ū╠ÄĪŻ¼F(xi©żn)─│▓┐ĻĀ▒Ż│ų┼cB,ĪóCā╔³cŽÓ═¼Ą─ŠÓļx┤®▀^æ(zh©żn)ł÷,Ż¼Ųõį┌ąą▀M(j©¼n)▀^│╠ųąŻ¼┼cA³cų«ķgūŅČ╠Ą─ŠÓļx×ķČÓ╔┘Ū¦├ū? ( )
A,Īó0.5 B,Īó0.6
CĪó0.7 D,Īó0.875
ĪŠĮŌ╬÷Ī┐C,ĪŻĄ┌ę╗▓ĮŻ¼▒ŠŅ}┐╝▓ķÄū║╬å¢Ņ},Ż¼ī┘ė┌ŲĮ├µÄū║╬ŅÉ,ĪŻĄ┌Č■▓ĮŻ¼╚ńłD╦∙╩Š,Ż¼▓┐ĻĀę¬▒Ż│ų┼cB,ĪóCā╔³cŽÓ═¼Ą─ŠÓļx┤®▀^æ(zh©żn)ł÷Ż¼╝┤╩Ūį┌BCā╔³cĄ─ī”ĘQ▌Sų▒ŠĆFO╔Žąą▀M(j©¼n),Ż¼BC⊥FO,ĪŻū÷AD⊥OFŻ¼AŠÓOFūŅČ╠Ą─ŠÓļx╝┤╩ŪAD,ĪŻė╔╣┤╣╔Č©└Ē┐╔ų¬BC=5,Ż¼ätBF=2.5ĪŻ
Ą┌╚²▓Į,Ż¼▀^A³cū÷BC╔ŽĄ─Ė▀AE,Ż¼─Ū├┤AE=AB×AC÷BC=3×4÷5=2.4ĪŻį┌ų▒ĮŪ╚²ĮŪą╬ABEųąBE²=AB²-AE²,Ż¼ätBE=1.8,ĪŻ┐╔Ą├AD=EF=BF-BE=2.5-1.8=0.7,ĪŻę“┤╦Ż¼▀xō±C▀xĒŚ,ĪŻ
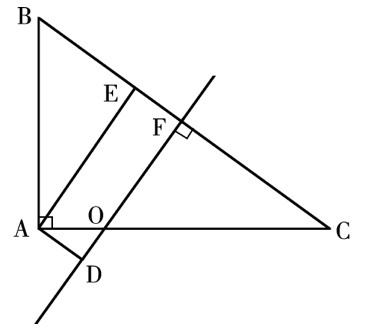
łD3
═©▀^╔Ž├µ╚²Ą└Ņ}─┐Ą─╩ŠĘČ,Ż¼ŽÓą┼Ė„╬╗┐╝╔·ī”ė┌«ŗłDĘ©Ū¾ĮŌ┐šķgÄū║╬å¢Ņ}Ą─╦╝┬Ęėą┴╦Ė³▀M(j©¼n)ę╗▓ĮĄ─šJ(r©©n)ūR,ĪŻÄū║╬å¢Ņ}Äū║§├┐─ĻĢ■┐╝▓ķę╗Ą└Ż¼ėą╣½╩ĮĘ©,Īó┴ą┼eĘ©,Īó«ŗłDĘ©Ą╚║▄ČÓĘĮĘ©Ż¼Ųõųą«ŗłDĘ©üĒĮŌøQ┐šķgÄū║╬å¢Ņ}╩Ū▒╚▌^ļyĄ─,Ż¼ŽŻ═¹┤¾╝ę┼¼┴”éõ┐╝,Ż¼│╔╣”╔Ž░Č!

ŽÓĻP(gu©Īn)ā╚(n©©i)╚▌═Ų╦]Ż║

┘Ną─┐╝╣½┐═Ę■

┘Ną─īŻī┘┐═Ę■
╔Žę╗Ų¬Ż║ąą£y┼ąöÓ═Ų└Ēų¬ūR³cŻ║ʱȩ┐ŽČ©╩Į

ł¾├¹Śl╝■?
ŹÅ╬╗▀xō±?
╣Pįć┐Ų─┐?
├µįćĘĮ╩Į?
......

 į┌ŠĆ┐═Ę■Ī┴
į┌ŠĆ┐═Ę■Ī┴

³cō¶╦∙ąĶ┘Y┴ŽŻ¼Æ▀┤aŅI(l©½ng)╚Ī








šą┐╝╣½Ėµ┐╝įć┤¾ŠV┬Ü╬╗▒Ēł¾├¹╚ļ┐┌£╩(zh©│n)┐╝ūC┤“ėĪ┐╝įćĢrķg│╔┐ā▓ķįā├µįć├¹å╬õøė├╣½╩Š┐╝įć┐ņėŹ