2021-05-26 16:57:13 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәкғОч·ЦФә
ОДХВҒнФҙЈәкғОч·ЦФә
ЎЎЎЎРРңyёчДЈүKЦР,Ј¬”ө(shЁҙ)БҝкP(guЁЎn)ПөҙуёЕКЗБоҙу¶а”ө(shЁҙ)ҝјЙъЧоо^МЫөДТ»ӮҖБЛЈ¬әЬ¶аҝјЙъФЪҝјҲцЙПЯx“сЦұҪУ·Е—ү,Ј¬ө«”ө(shЁҙ)БҝкP(guЁЎn)ПөЖдҢҚКЗұЈЧCОТӮғДЬ·сЯMГжөДТ»ӮҖкP(guЁЎn)жI,Ј¬ҝјФҮЦРҝЙТФЯx“сЧцТ»Р©әҶҶОөДо}Дҝ,Ј¬ҪсМмЛщХfөД№ӨіМҶ–о}ЦРөДР§ВКЦЖјsРНоҗөДо}ДҝҝјФҮЦРіц¬F(xiЁӨn)лy¶ИТ»°гІ»ҙуЈ¬ҝЙТФФЪЖҪ•rөД•rәтПВ№Ұ·тХЖОХЦ®әу,Ј¬ҝјҲцЙПҫНҝЙТФҝмЛЩЧціцҒн,ЎЈ

ЎЎЎЎТ»Ўў о}РНЧR„e
ЎЎЎЎо}ёЙЦРУРҪoіцІ»Н¬ЦчуwөДР§ВКөДұИАэкP(guЁЎn)Пө»тұ¶”ө(shЁҙ)кP(guЁЎn)Пө
ЎЎЎЎ¶ю,Ўў Ҫво}ЛјВ·
ЎЎЎЎ·Ҫ·ЁЈәЩxЦө·Ё
ЎЎЎЎҪво}ІҪуEЈәўЩёщ“ю(jЁҙ)ұИАэкP(guЁЎn)ПөЩxЦөР§ВК;
ЎЎ�,ЎўЪУӢЛг№ӨЧчҝӮБ�;
ЎЎЎЎўЫёщ“ю(jЁҙ)о}ТвЗуҪв,ЎЈ
ЎЎЎЎИэ,Ўў Хжо}ЦvҪв
ЎЎЎЎЎҫАэ1ЎҝУРјЧЎўТТ,ЎўұыИэӮҖ№ӨЧчҪM,Ј¬ТСЦӘТТҪM2МмөД№ӨЧчБҝЕcјЧЎўұы№ІН¬№ӨЧч1МмөД№ӨЧчБҝПаН¬,ЎЈA№ӨіМИзУЙјЧ,ЎўТТҪM№ІН¬№ӨЧч3МмЈ¬ФЩУЙТТ,ЎўұыҪM№ІН¬№ӨЧч7Мм,Ј¬ХэәГНкіЙЎЈИз№ыИэҪM№ІН¬НкіЙ,Ј¬РиТӘХы7Мм,ЎЈB№ӨіМИзұыҪMҶОӘҡНкіЙХэәГРиТӘ10МмЈ¬Ҷ–ИзУЙјЧ,ЎўТТҪM№ІН¬НкіЙ,Ј¬РиТӘ¶аЙЩМм?
ЎЎЎЎA. І»өҪ6Мм
ЎЎЎЎB.6Мм¶а
ЎЎЎЎC. 7Мм¶а
ЎЎЎЎD. і¬Я^8Мм
ЎЎЎЎХэҙ_ҙр°ёЈә C
ЎЎЎЎЎҫҪвОцЎҝөЪТ»ІҪЈ¬ұҫо}ҝјІй№ӨіМҶ–о},Ј¬ҢЩУЪР§ВКЦЖјsРНо}Дҝ,Ј¬УГЩxЦө·ЁҪво}ЎЈ
ЎЎЎЎөЪ¶юІҪ,Ј¬ФO(shЁЁ)ИэХЯ№ӨЧчР§ВК·Ц„eһйјЧ,ЎўТТЎўұы,Ј¬ёщ“ю(jЁҙ)о}Тв„tУР2ТТ=јЧ+ұы,Ј¬3(јЧ+ТТ)+7(ТТ+ұы)=7(јЧ+ТТ+ұы)Ј¬ҝЙөГ3ТТ=4јЧ,Ј¬ЩxЦөјЧ=3,Ј¬„tТТ=4Ј¬ҪвөГұы=5ЎЈ
ЎЎЎЎөЪИэІҪ,Ј¬B№ӨіМҝӮБҝ=10ұы=10×5=50,Ј¬„tјЧТТәПЧчРиТӘ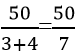 МмЈ¬јҙ7Мм¶а,ЎЈ
МмЈ¬јҙ7Мм¶а,ЎЈ
ЎЎЎЎТтҙЛ,Ј¬Яx“сCЯxн—ЎЈ
ЎЎЎЎЎҫАэ2ЎҝДіҶОО»јЧ,ЎўТТ,ЎўұыИэИЛШ“ШҹХыАнТ»н—ҷn°ёЈ¬ЛыӮғ№ӨЧч5МмНкіЙБЛ1/4,Ј¬Ц®әујЧәНТТТтЖдЛы№ӨЧчұ»Х{(diЁӨo)лx,Ј¬ғЙМмәуІЕ·ө»ШЈ¬ЖЪйgұыА^Аm(xЁҙ)ХыАнҷn°ё,ЎЈТСЦӘјЧ,ЎўТТЎўұыИэИЛөД№ӨЧчР§ВКЦ®ұИһй4ЎГ3ЎГ2,Ј¬„tНкіЙЯ@н—№ӨЧч№ІРиТӘ»ЁЩM( )Мм
ЎЎЎЎA. 20
ЎЎЎЎB. 21
ЎЎЎЎC. 22
ЎЎЎЎD. 23
ЎЎЎЎХэҙ_ҙр°ёЈәC
ЎЎЎЎЎҫҪвОцЎҝөЪТ»ІҪ,Ј¬ұҫо}ҝјІй№ӨіМҶ–о}Ј¬ҢЩУЪР§ВКЦЖјsРНо}Дҝ,Ј¬УГЩxЦө·ЁҪво},ЎЈ
ЎЎЎЎөЪ¶юІҪЈ¬ЩxЦөјЧөДР§ВКһй4,Ј¬ТТөДР§ВКһй3,Ј¬ұыөДР§ВКһй2ЎЈ№ӨЧчҝӮБҝ=4×5×(4+3+2)=180,Ј¬ЖдЦРУР2МмКЗұыҶОӘҡёЙ,Ј¬№ӨЧчБҝһй2×2=4Ј¬КЈУаөД№ӨЧчБҝУЙјЧТТұыәПЧчёЙРиТӘЈә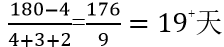 ,Ј¬јҙ20Мм,ЎЈДЗГҙТ»№ІРиТӘ20+2=22МмЎЈ
,Ј¬јҙ20Мм,ЎЈДЗГҙТ»№ІРиТӘ20+2=22МмЎЈ
ЎЎЎЎТтҙЛ,Ј¬Яx“сCЯxн—,ЎЈ
ЎЎЎЎЎҫАэ3ЎҝТ»ҲцҙуС©Я^әуЈ¬ДіҶОО»Ри°ІЕЕҶT№ӨЗе’Я°ьёЙ…^(qЁұ)өДөАВ··eС©,ЎЈЗе’Я•rұШнҡ3ИЛТ»ҪM,Ј¬ЖдЦР2ИЛзPС©,Ј¬1ИЛ’ЯС©,ЎЈИз№ы°ІЕЕ10ИЛзPС©Ј¬3.5РЎ•rІЕДЬНкіЙЎЈјЩФO(shЁЁ)ГҝҪM№ӨЧчР§ВКПаН¬,Ј¬ИфТӘФЪ100·ЦзҠғИ(nЁЁi)НкіЙ,Ј¬„tРи°ІЕЕөДҶT№ӨИЛ”ө(shЁҙ)ЧоЙЩКЗЈә
ЎЎЎЎA. 21
ЎЎЎЎB. 24
ЎЎЎЎC. 30
ЎЎЎЎD. 33
ЎЎЎЎХэҙ_ҙр°ёЈәD
ЎЎЎЎЎҫҪвОцЎҝөЪТ»ІҪЈ¬ұҫо}ҝјІй№ӨіМҶ–о},Ј¬ҢЩУЪР§ВКЦЖјsРНо}Дҝ,Ј¬УГЩxЦө·ЁҪво}ЎЈ
ЎЎЎЎөЪ¶юІҪ,ЩxЦөГҝҪMГҝРЎ•rөД№ӨЧчР§ВКһй1,Ј¬10ИЛзPС©№ІУР5ҪM,Ј¬„t№ӨЧчҝӮБҝһй5×3.5=17.5Ј¬100·ЦзҠ=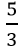 РЎ•r,Ј¬„tЦБЙЩРиТӘ17.5÷
РЎ•r,Ј¬„tЦБЙЩРиТӘ17.5÷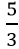 =10.5(ҪM),Ј¬јҙ11ҪMЎЈ
=10.5(ҪM),Ј¬јҙ11ҪMЎЈ
ЎЎЎЎөЪИэІҪ,Ј¬ЛщТФРи°ІЕЕөДҶT№Ө”ө(shЁҙ)һй11×3=33(ИЛ),ЎЈ
ЎЎЎЎТтҙЛЈ¬Яx“сDЯxн—,ЎЈ
ЎЎЎЎТФЙПҫНКЗ№ӨіМҶ–о}ЦРөДР§ВКЦЖјsРНҶ–о}өДТ»Р©Зйӣr,Ј¬Я@оҗРНо}ДҝУРөД•rәт•юЦұҪУҪo¶ЁР§ВКөДұИЦөЈ¬АэИзЈәјЧТТР§ВКЦ®ұИКЗ2Јә3,Ј¬УРөД•rәт•юйgҪУҪoіцР§ВКөДұИЦө,Ј¬АэИзЈәјЧ3МмөД№ӨЧчБҝөИУЪТТ4МмөД№ӨЧчБҝЈ¬УРөД•rәтёьКЗРиТӘНЖҢ§іцР§ВКөДұИЦө,Ј¬ҪвЯ@оҗо}ДҝкP(guЁЎn)жIКЗТӘДЬЧR„eіцо}РН,Ј¬°ҙұИАэҪoР§ВКЩxЦөЈ¬И»әуУӢЛг№ӨЧчҝӮБҝ,Ј¬ёщ“ю(jЁҙ)о}ТвЗуҪв,ЎЈ


ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБПЈ¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ