2021-05-26 10:19:03 №«„ХҶTҝјФҮҫW 
 ОДХВҒнФҙЈәЙҪОч·ЦФә
ОДХВҒнФҙЈәЙҪОч·ЦФә
ЎЎЎЎФЪҪьҺЧДкөДКЎҝј®”ЦРЈ¬лSЦш”өБҝҶ–о}Хыуwлy¶ИөДЙПЙэ,Ј¬РРіМҶ–о}ТІПтЦшёьлyЯ~іцБЛІҪ·Ҙ,ЎЈФЪЯ@ҳУөДЗйӣrПВЈ¬ЦұҫҖРН¶аҙОПаУцҶ–о}өДіц¬FҫНЧғөГоl·ұБЛЖрҒн,ЎЈҪсМм,Ј¬ИAҲDҪМУэҫНһйҙујТ?guЁ©)§ҒнЦұҫҖРН¶аҙОПаУцҶ–о}өДҪво}·Ҫ·ЁЈ¬ЧҢОТӮғДЬУГ№«КҪҪвӣQҙЛоҗо}Дҝ,ЎЈ
ЎЎЎЎОТӮғПИҒн»ШоҷТФПВОТӮғЦ®З°ЛщҢWөДҶОҙОПаУцҶ–о},ЎЈИзҲDЛщКҫЈәҢҰУЪҶОҙОПаУцЈ¬ОТӮғҝЙТФАнҪвһйғЙИЛ№ІН¬ЧЯНкБЛЯ@¶ОВ·,Ј¬јҙҝӮВ·іМһйВ·іМәН,ЎЈөГөҪ№«КҪ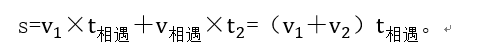

ЎЎЎЎЯҖКЗН¬ҳУөДЗйҫ°Ј¬®”ғЙИЛҸДA,Ј¬BғЙ°¶ПаПт¶шРРй_Кј,Ј¬ОТӮғТ»ЦұІ»НЈЦ№өДФ’ҫН»ШөГөҪПВҲDЈә
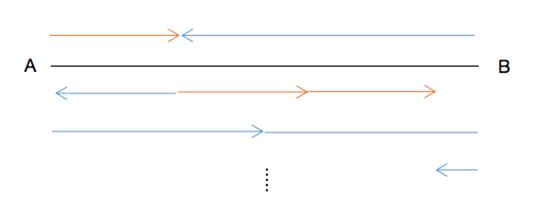
ЎЎЎЎОТӮғҝЙТФ°l(fЁЎ)¬FЈәөЪТ»ҙОПаУцКЗғЙИЛәПЧчЧЯНкБЛТ»ҙОЯ@¶ОВ·өДФ’,Ј¬ҸДөЪТ»ҙОПаУцөҪөЪ¶юҙОПаУцЈ¬ОТӮғҝЙТФТ•һйғЙИЛәПЧчЧЯНкБЛғЙҙОЯ@¶ОВ·,ЎЈ¶шЗТ,Ј¬ҸДөЪ¶юҙОПаУцөҪөЪИэҙОПаУцЈ¬ТІҝЙТ•һйғЙИЛәПЧчЧЯНкБЛғЙҙОЯ@¶ОВ·,ЎЈ
ЎЎЎЎИф°СПаУцҙО”өФOһйn,Ј¬І»ҝј‘]өЪТ»ҙОПаУцөДЗйӣrЈ¬ДЗҝЙТФөГөҪПа‘Ә№«КҪЈә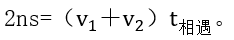
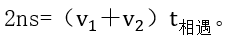
ЎЎЎЎәНЦ®З°өД№«КҪЯBБў,Ј¬ОТӮғјҙҝЙөГөҪлp°¶РНПаУц№«КҪЈә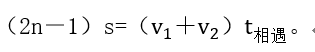
ЎЎЎЎіэҙЛЦ®Нв,Ј¬ЯҖУРТ»·NДЈРНЈәғЙИЛҸДН¬Т»ьcіц°l(fЁЎ)Ј¬ҢҰ‘ӘөГ,Ј¬ОТӮғ·QЦ®һйҶО°¶РНПаУцДЈРН,ЎЈИзҲDЛщКҫЈә
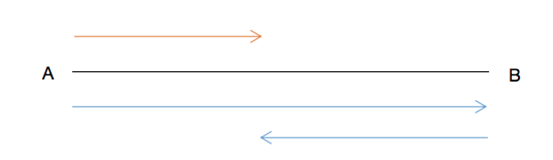
ЎЎЎЎҢҰУЪПаУцЯMРРУ‘Х“ЈәҝЙТ•һйғЙИЛ№ІН¬ЧЯНкБЛғЙҙОИ«В·іМЈ¬Иф°СПаУцҙО”өФOһйn,Ј¬ҝЙУГ№«КҪЈә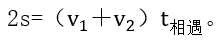
ЎЎЎЎ¶шЦ®әуФЩУРПаУц,Ј¬„tәНлp°¶РНәу°лІҝ·ЦПаН¬Ј¬қMЧг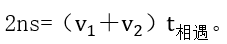 ЎЎЎЎғЙКҪІўІ»ӣ_Н»,ЎЈ
ЎЎЎЎғЙКҪІўІ»ӣ_Н»,ЎЈ
ЎЎЎЎФЪН¬ьcіц°l(fЁЎ)өДЗйӣrПВ,Ј¬іэН¬Птіц°l(fЁЎ)Ц®НвЈ¬ЯҖҝЙУР®җПтіц°l(fЁЎ),Ј¬ЖдВ·ҫҖҲDәНөЪ¶юҙОПаУцЦ®әуөДҲDКҫНкИ«Т»ЦВ,Ј¬јҙһйЈә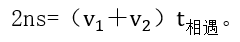
ЎЎЎЎ№КҶО°¶РНПаУц№«КҪһйЈә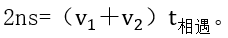
ЎЎЎЎЎҫАэ1ЎҝјЧТТғЙИЛФЪПаҫа120ГЧөДЦұВ·ЙПҒн»ШЕЬІҪЈ¬ЛыӮғН¬•rҸДЦұВ·өДғЙ¶Ліц°l(fЁЎ),ТСЦӘјЧТТөДЛЩ¶ИұИһй7:5,Ј¬„t®”ғЙИЛөЪ¶юҙОПаУц•r,Ј¬јЧЧЯБЛ¶аЙЩГЧ?
ЎЎЎЎA.210
ЎЎЎЎB.240
ЎЎЎЎC.270
ЎЎЎЎD.290
ЎЎЎЎЯ@өАо}Ј¬ФЪОТӮғҢWБ•БЛЦұҫҖРН¶аҙОПаУцҶ–о}Ц®әуұгөГәҶҶОБЛЖрҒн,ЎЈКЧПИ,Ј¬НЁЯ^Чxо}ОТӮғҝЙТФЕР¶ЁЯ@КЗТ»өАлp°¶РНөДЦұҫҖПаУцҶ–о}Ј¬ЛщУГөҪөД№«КҪҫНКЗЈә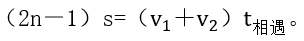
ЎЎЎЎОТӮғҝЙТФАнҪвһйЈәјЧТТғЙИЛәПЧчЧЯНкБЛ3ӮҖ120ГЧ,Ј¬УЙУЪҸДЯ\„Уй_КјөҪЯ\„УҪYКшЈ¬јЧТТғЙИЛҫщһйНЈЦ№Я\„У,Ј¬ЛщТФҝЙТФК№УГұИАэкPПөЈәФЪ•rйgІ»ЧғөДЗйӣrПВ,Ј¬ЛЩ¶ИЕcВ·іМіЙХэұИЈ¬өГөҪЈәУЙУЪјЧТТғЙИЛЛЩ¶ИЦ®ұИһй7:5,Ј¬№КјЧТТғЙИЛВ·іМЦ®ұИТІһй7:5,ЎЈ
ЎЎЎЎҪYәП3ӮҖ120ГЧөДРЕПўЈ¬ҝЙТФөГөҪЈәјЧЧЯЯ^өДВ·іМһй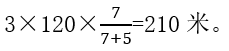
ЎЎЎЎТтҙЛ,Ј¬ҙр°ёЯx“сAЯxн—,ЎЈ
ЎЎЎЎЎҫАэ2ЎҝРЎҸҲ,ЎўРЎНх¶юИЛН¬•rҸДјЧөШіц°l(fЁЎ)Ј¬с{ЬҮ„тЛЩФЪјЧТТғЙөШЦ®йgНщ·өРРсӮ,ЎЈРЎҸҲөДЬҮЛЩұИРЎНхҝм,Ј¬ғЙИЛіц°l(fЁЎ)әуөЪТ»ҙОәНөЪ¶юҙОПаУц¶јФЪН¬Т»өШьcЈ¬ДЗГҙРЎҸҲөДЬҮЛЩКЗРЎНхөД¶аЙЩұ¶Јә
ЎЎЎЎA.3
ЎЎЎЎB.1.5
ЎЎЎЎC.2
ЎЎЎЎD.2.5
ЎЎЎЎЧxо}Ц®әуЕР”ао}РНһйҶО°¶РНөДЦұҫҖПаУцҶ–о},Ј¬ЛщУГөҪ№«КҪЈә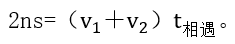
ЎЎЎЎо}ДҝөДҶ–о}ФЪФғҶ–РЎҸҲәНРЎНхөДЛЩ¶ИЦ®ұИ,ЎЈФЪо}ДҝЦРӣ]УРіц¬FЛЩ¶И”ө“юөДЗйӣrПВЈ¬Т»°гҝј‘]УГұИАэкPПөҪво},ЎЈУЙУЪИ«іМРЎҸҲәНРЎНх¶јӣ]УРРЭПў,Ј¬№КФЪ•rйgТ»¶ЁөДЗйӣrПВЈ¬ЛЩ¶ИәНВ·іМіЙХэұИ,Ј¬№КҝЙҢўо}ДҝЮD»ҜһйҢҰВ·іМЦ®ұИөДЗуҪв,ЎЈ
ЎЎЎЎҢҰРЎНхөДВ·іМЯMРР·ЦОцЈ¬јЩФOХfРЎНхөЪТ»ҙОПаУцРРсӮБЛxөДҫалx,Ј¬ДЗГҙ,Ј¬®”өЪ¶юҙОПаУцөД•rәтЈ¬ЛыУЦ»ШөҪБЛөЪТ»ҙОПаУцөДөШьc,Ј¬ҪYәПЖдЛЩ¶ИЭ^Вэ,Ј¬№КЖд‘ӘФ“КЗҸДіц°l(fЁЎ)Т»¶ОөҪЯ_БЛБнТ»¶ОЈ¬УЦ·ө»ШБЛПаУцьc,Ј¬В·іМ‘ӘһйІоТ»ӮҖxҫНХэәГЕЬНкғЙҙОјЧТТғЙөШ,Ј¬№КЖдВ·іМҝЙұнКҫһй(2s-x)ЎЈ
ЎЎЎЎҸДөЪТ»ҙОПаУцй_КјөҪөЪ¶юҙОПаУц,Ј¬УЙУЪРЎНхәНРЎҸҲөДЛЩ¶ИҫщһйёДЧғ,Ј¬¶шЗТВ·іМәНТІһй2sЈ¬№КРЎНхРРЧЯөДВ·іМТАИ»һйx,ЎЈ
ЎЎЎЎ»ШоҷХыӮҖЯ^іМ,Ј¬ғЙИЛ№ІН¬ЧЯНкБЛ4sЈ¬РЎНхҶОИЛВ·іМһй2x,Ј¬№КРЎҸҲҶОИЛВ·іМһй(4s-2x),ЎЈҪYәПРЎНхөДВ·іМһй(2s-x)Ј¬№К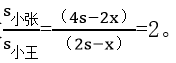
ЎЎЎЎТтҙЛ,Ј¬ҙр°ёЯx“сCЯxн—,ЎЈ
ЎЎЎЎҪӣЯ^ғЙөААэо}өДЦvҪвЈ¬ПаРЕҙујТҢҰУЪЦұҫҖРНПаУцҶ–о}ТСҪӣУРБЛЧФјәөДБЛҪв,Ј¬ФЪОДХВөДЧоәу,Ј¬РЎҫҺҪoҙујТБфТ»ӮҖҶ–о}Ј¬јЩИзФЪТ»°ЩГЧЕЬөАЙП,Ј¬Т»О»ЧшЭҶТОөДАПМ«М«әН„ўПиҸДғЙ¶Ліц°l(fЁЎ),Ј¬ПаПт¶шРРЧцНщ·өЯ\„У,Ј¬ДЗГҙХҲҶ–Ј¬ФЪөЪ¶юҙОПаУцөД•rәт,Ј¬ЛыӮғғЙИЛөДВ·іМәНКЗ300ГЧГҙ?
ЎЎЎЎБфӮҖРЎОІ°Н,Ј¬ОТӮғПВЖЪФЩТҠ!

ПакPғИИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю
ЙПТ»ЖӘЈәРРңyЦӘЧRьcЈә»щЖЪұ¶”ө,Ўў»щЖЪұИЦШЎў»щЖЪЖҪҫщ”өо}РНҪвОц
ПВТ»ЖӘЈәРРңyЦӘЧRьcЈә№ӨіМҶ–о}Ц®Ҫo¶Ё•rйgРНәНР§ВКЦЖјsРНо}РНҪвОц

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ