2021-03-15 18:06:55 ¿¨íT¢¥åƒW(w´Èng) 
 öáíôÚåÇȤàAD§äÆ»
öáíôÚåÇȤàAD§äÆ»
¡¼ö£ë˜W,Ș§y(t´₤ng)£IŸ}òúç(sh´Ç)ê¢õP(gu´Àn)üçøÅçá�,È¢¥ý¢ñøȘ§y(t´₤ng)£IŸ}øÅèÌ¥¯ç§çáøˆæR■cÝàï^Šs,Șç¨òúǵ¥Øý£Øˆ£é,Șû¢Ø£Ÿ}ÅëâÿûÌÑ¥ÆÅ¿äÑ´çá§ãŸ}ñ§ñ´È˜§ÆüôÚàAD§äƻأóÞÚ§ØûÄØ£üô§y(t´₤ng)£IŸ}øÅçáÄöÿ¥₤øÅŸ},ÀÈ
1.òýûÇòúÄöÿ¥₤øÅŸ}
Äöÿ¥₤øÅŸ}¥Ç¥₤øŧy(t´₤ng)£IŸ},Șòúø¡åÖÂÄöÿ¥₤øÅçáë˜rȘò¿çûÄöÿçáÔ\ìMæŸòÀ,ÀÈàÓüôûÌ⻟}Ȥ
⻟}ȤåÖØ£l¿¨ôñèüû¢¡¶100úÏûæÆÅØ£æª}š,Ș¿ýÆÅ5}šÈ˜Ø£ä}šÇÌÆÅ10Äöÿ,Șѱä}šÇÌÆÅ20Äöÿ,ȘöÍä}šÇÌÆÅ40ÄöÿȘóðÆÁè}šòú¢íçá�,ȘF(xi´Ên)åÖ؈¯îùªÆÅçáÄöÿ¥₤øÅÇÌñéåÖØ£}šâÿ,ȘàÓ¿«û¢ÄöÿÔ\ï1¿¨âÿÅÒ؈0.5åˆÍXȘtæŸèìÅÒ؈ÑÁèìÔ\ìM?
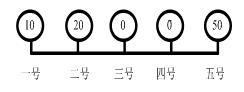
A.4500åˆ B.5000åˆ C.5500åˆ D.6000åˆ
2.Äöÿ¥₤øÅŸ}æþîÙçáåÙt
¥ÇåÖñúÕ]¤üçáôñ§èü(àÓƒÅö,ÀÂðÅöçà)ÆÅÑÁ“■c”,Ș■cèüÆÅأѴøÄê¢çáÄöÿȘû¢■cøÛÕgÆèأѴçáôñ§ÔB§Æ,Ș¯ÇííæŸ(y´Ùu)çáñ§ò§¯îÄöÿ¥₤øÅç§Ø£■cèüæþîÙçá§ãŸ}åÙtȤÇ_Ñ´ôñøÅÕgçáàöØãØ£■c,ȘéÅÁå■cèÑùÄöÿçá¢øÄê¢È˜¯îïpçáØ£Ñùü·øÄçáØ£Ñù¥₤øÅ,ÀÈæÂØãȤåÖQÑ´Äöÿ몤öä¥₤øÅr,ȘóÞQÑ´æ¼ÆûçáòúÄöÿçáøÄê¢È˜øêÆÖƒÁŠxHHòúÕêùÆùÐÔ\ìM,ÀÈ
áúàÓ¤ö§ãQèüûÌçá⻟}áÄ?öØØ£óÞ¢ÇØ£üô,ÀÈ
â«Æû§ãŸ}åÙtȘ¢èøˆ,Ș݃Ÿ}ùál“ôñ”Ñ¥ƒÔð“æµÔ ¢øÄê¢ïpÆÖÆØÔ ¢øÄꢔçál¥±,ȘùªØåÔ@Åˋôñèüçáê¼ë´ñ§ò§Ñ¥òúáæµç§ÆØȘطÇù¥₤øÅç§öÍä}šòúæŸ(y´Ùu)Ôxþ,ÀÈ¥ÇüàåÖØ£ä¤ëѱäøÅÕgàöÔxØ£■c,ȘæµÔ øÄꢢ¤ëÕ10ȘÆØÔ øÄꢢ¤ë70,ȘæµÔ ¢øÄê¢ïpÆÖÆØÔ ¢øÄê¢,ȘطÇù؈¯îØ£ä}šçá10çáÄöÿØóÆç§Ñ±ä}š,ȘÔ@Æѱä}šƒëüÁÛÆÖÆÅêù30ÄöÿÀÈÇùråÖѱäà»ä}šøÅÕgÇ_Ñ´àöØãØ£■c,ȘæµÔ øÄꢢ¤ëÕ30,ȘÆØÔ øÄꢢ¤ë50ȘæµÔ ¢øÄê¢ïpÆÖÆØÔ ¢øÄê¢,ȘطÇùåì¯îѱä}šçá30ÄöÿØóÆç§à»ä}š,ȘØâÇöŸëóȘÅÒ؈ùªÆÅÄöÿØóÆç§öÍä}š,ȘÇùrÅÒ؈Ô\ìM(10×400+20×300)×0.5=5000åˆ,ȘÔxBÀÈ

üÁõP(gu´Àn)à(n´´i)àïëóù]Ȥ

ìNÅᢥ¿¨¢ëñ±

ìNÅáÈì¢ëñ±
èüØ£óˆÈ¤2021áõ¡È§´¿¨íT¢¥åȤأŸ}à»ò§ÀˆÀˆ§äáÐóó§ãÅÅyç(sh´Ç)ê¢õP(gu´Àn)üç
üôØ£óˆÈ¤2021áõåóáüÅÅyç(sh´Ç)ê¢õP(gu´Àn)üçȤ¯l(f´À)]üŠüµêÎȘ§ãQÀ¯æŸý£â«åÙtÀÝŸ}

µû«l¥±?
ö£Ôxþ?
¿På¢óá¢?
ûÌåñ§ò§?
......

 åÖƒ¢ëñ±Àê
åÖƒ¢ëñ±Àê

■c¶ùªÅÒìYêü,ȘÔÇaŸI(l´¨ng)àÀ







