2022-03-02 13:07:57 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂí(lšąi)ÔŽŁș°Č»Ő·ÖÔș
ÎÄŐÂí(lšąi)ÔŽŁș°Č»Ő·ÖÔș

ó(bš€o)żŒ(wššn)î}œâ»óŁż
ÍŹW(xušŠ)ߎaŚÉÔ

ëx2022Äê°Č»ŐÊĄżŒßÓĐČ»”œ40Ìì,ŁŹÍŹW(xušŠ)”ÄäżŒ»ù±ŸÒŃœ(jš©ng)”œÁËČéȱŃa(bšł)©”Äh(hušąn)č(jišŠ),ŁŹŠ(dušŹ)ÓÚÄÇĐ©»ù”A(chšł)î}ĐÍ”ÄÓ(jšŹ)ËăŒŒÇÉșÍč«ÊœŁŹÏàĐĆŽóŒÒÒŃœ(jš©ng) ÊìÓÚĐŰÁË,ŁŹËùÒÔŹF(xiš€n)ÔÚŸÍĐèÒȘŠ(dušŹ)ÓÚÒ»Đ©ÔÚżŒÔÖĐłöŹF(xiš€n)îlÂÊ]ÓĐß@ĂŽŽó”ÄżŒüc(dišŁn)șÍŒŒÇÉßM(jšŹn)ĐĐÍŰŐčW(xušŠ)Á(xšȘ)ĄŁ
ĆŁłÔČĘ(wššn)î}Æä(shšȘ)À(yšąn)žńÒâÁxÉÏí(lšąi)Őf(shuš)Ș(yš©ng)ÔœĐŚöĆŁłÔČĘÄŁĐÍ,ŁŹÎÒÓĂÒ»·NÍšËŚÒŚ¶ź”ıÈÓśąÒ»Đ©É挰”œÔÊŒč̶šÁżÊÜ”œÉ(gšš)ÒòËŰ”ÄÓ°í”Ä»ù”A(chšł)Ș(yš©ng)ÓĂî}ȚD(zhušŁn)»ŻéŚ·Œ°(wššn)î}ĄŁÔÏëÒ»ÏÂ,ŁŹÎÒżÉÒÔ°ŃČĘ”ŰÉÏËùÓĐ”ÄČĘ°Îłöí(lšąi)ŁŹąÆäĆĆÁĐÔÚÒ»lÖ±ŸÉÏ,ŁŹÎÒœüËÆżÉÒÔżŽłÉÒ»l·,ŁŹĆŁÔړ·””ÄÒ»¶Ëé_ÊŒłÔČĘŁŹ¶űČĘéÁËČ»±»łÔčâÒÔÉúéL(zhšŁng)”Ä îB(tš€i)ÌÓëxĆŁ,ĄŁß@ÓŸÍŚłÉÁËŚ·Œ°(wššn)î},ĄŁ
ĆŁłÔČĘ(wššn)î}Ò»čȿɷÖéÈęîŁșč©Č»Ș(yš©ng)ÇóĄąč©ŽóÓÚÇóșÍč©ÇóÏà”È,ŁŹÏÂĂæÎÒí(lšąi)ÔŒ(xšŹ)Őf(shuš)Ò»ÏÂß@Èęîî}ĐÍÔÈçșÎœâŽđ,ĄŁ
č©Č»Ș(yš©ng)ÇóĄŁ
ÄÁö(chšŁng)ÉÏÓĐÒ»ÆŹòËÙÉúéL(zhšŁng)”ÄČĘ”Ű,ŁŹ·ĆNî^ĆŁÈ„łÔČĘÇÒĂżî^ĆŁĂżÌìłÔ”ÄČĘÁżÏàÍŹ,ĄŁĆŁłÔČĘÊčČĘÁżpÉÙŁŹČĘŚÔÉíÉúéL(zhšŁng)ÊčČĘÁżÔöŒÓ,ŁŹ(Ç°ÌáŁșĆŁłÔČĘ”ÄËٶȎóÓÚČĘŚÔÉíÉúéL(zhšŁng)”ÄËÙ¶È),ŁŹß@·NÇér·QÖźéč©Č»Ș(yš©ng)ÇóĄŁŒÙÔO(shšš)TÌìĆŁ°ŃČĘłÔÍê,ŁŹÍŹr(shšȘ)ŒÙÔO(shšš)ß@ÆŹČĘö(chšŁng)ÔÓĐÁżéy·Ę,ŁŹĂżî^ĆŁĂżÌìłÔ1·ĘČĘŁŹß@ÆŹČĘö(chšŁng)”ÄČĘĂżÌì”ÄÉúéL(zhšŁng)ËÙ¶Èéx·Ę,ĄŁtÔÓĐČĘÁż=(ĆŁĂżÌìłÔ”ô”ÄÁż-ČĘĂżÌìÉúéL(zhšŁng)”ÄÁż)×Ìì”(shšŽ),ŁŹŐûÀíżÉ”ĂŁșy=(N-x)×TĄŁ
ĄŸÀę1ĄżÄłÒßĂçœÓ·Nüc(dišŁn)ÊĐĂńŐęÔÚÓĐĐòĆĆê (dušŹ)”ÈșòœÓ·N,ĄŁŒÙÔO(shšš)ÖźșóÿХr(shšȘ)ĐÂÔöÇ°í(lšąi)œÓ·NÒßĂç”ÄÊĐĂńÈË”(shšŽ)ÏàÍŹ,ŁŹÇÒĂż(gšš)œÓ·NĆ_(tšąi)”ÄЧÂÊÏàÍŹŁŹœ(jš©ng)y(cšš)ËăŁșÈôé_8(gšš)œÓ·NĆ_(tšąi),ŁŹ6ĐĄr(shšȘ)șóČ»ÔÙÓĐÈËĆĆê (dušŹ);Èôé_12(gšš)œÓ·NĆ_(tšąi),ŁŹ3ĐĄr(shšȘ)șóČ»ÔÙÓĐÈËĆĆê (dušŹ)ĄŁÈçčûÿХr(shšȘ)ĐÂÔö”ÄÊĐĂńÈË”(shšŽ)±ÈŒÙÔO(shšš)”Ķà25%,ŁŹÄÇÎ鱣ŚC2ĐĄr(shšȘ)șóČ»ÔÙÓĐÈËĆĆê (dušŹ),ŁŹĐèé_œÓ·NĆ_(tšąi)”Ä”(shšŽ)ÁżÖÁÉÙéŁș
A.14(gšš)B.15(gšš)
C.16(gšš)D.17(gšš)
ĄŸœâî}ˌ·Ąż
žùț(jšŽ)ĆŁłÔČĘč«Êœy(tšŻng)=(N-x)TŁŹyŽú±íÔÓĐČĘÁż,ŁŹŒŽÔÓĐĆĆê (dušŹ)”ÄÊĐĂń”(shšŽ);NŽú±íĆŁ”Äî^”(shšŽ),ŁŹŒŽËùé_œÓ·NĆ_(tšąi)”(shšŽ)Áż;xéČĘÉúéL(zhšŁng)”ÄËÙ¶ÈŁŹŒŽĂżĐĄr(shšȘ)ĐÂÔöÊĐĂń”(shšŽ);TŽú±ír(shšȘ)ég,ĄŁŽúÈë”(shšŽ)ț(jšŽ),ŁŹy=(8-x)×6ŁŹy=(12-x)×3,ŁŹœâ”Ăx=4,ŁŹy=24,ŁŹĂżĐĄr(shšȘ)ĐÂÔöÊĐĂńÈË”(shšŽ)ÔöŒÓ25%ŁŹtxŚ?yšu)?×(1+25%)=5,ŁŹÔO(shšš)ÖÁÉÙĐèé_N(gšš)œÓ·NĆ_(tšąi)ÄܱŁŚC2ĐĄr(shšȘ)Č»ÔÙÓĐÈËĆĆê (dušŹ),ŁŹŽúÈëč«Êœ”ĂŁș24=(N-5)×2,ŁŹœâ”ĂN=17,ĄŁßxDĄŁ
č©ŽóÓÚÇó,ĄŁ
ÄÁö(chšŁng)ÉÏÓĐÒ»ÆŹòËÙÉúéL(zhšŁng)”ÄČĘ”Ű,ŁŹ·ĆNî^ĆŁÈ„łÔČĘÇÒĂżî^ĆŁĂżÌìłÔ”ÄČĘÁżÏàÍŹĄŁĆŁłÔČĘÊčČĘÁżpÉÙ,ŁŹČĘŚÔÉíÉúéL(zhšŁng)ÊčČĘÁżÔöŒÓ,ŁŹ(Ç°ÌáŁșĆŁłÔČĘ”ÄËÙ¶ÈĐĄÓÚČĘŚÔÉíÉúéL(zhšŁng)”ÄËÙ¶È)ŁŹß@·NÇér·QÖźéč©ŽóÓÚÇó,ĄŁŒÙÔO(shšš)TÌìÖźșó,ŁŹČʔ۔ÄĂæ·eÔöŒÓÁËyŁŹĂżî^ĆŁĂżÌìłÔ1·ĘČĘ,ŁŹß@ÆŹČĘö(chšŁng)”ÄČĘĂżÌì”ÄÉúéL(zhšŁng)ËÙ¶Èéx·Ę,ĄŁtČĘ”ŰÔöŒÓ”ÄĂæ·e=(ČĘĂżÌìÉúéL(zhšŁng)”ÄÁż-ĆŁĂżÌìłÔ”ô”ÄÁż)×Ìì”(shšŽ)ŁŹŐûÀíżÉ”ĂŁșy=(x-N)×T,ĄŁ
ĄŸÀę2ĄżŒÙÔO(shšš)Ò»ÆŹÄÁö(chšŁng)”ÄÇàČĘÒ»Ö±¶ŒÊÇ“òËÙ”ŚÔÈ»ÉúéL(zhšŁng)”ÄŁŹÔÄÁö(chšŁng)3ÔÂłő·ĆđB(yšŁng)ÓĐ1000Ö»Ńò,ŁŹ30ÌìșóÇàČʔĿÁżŚ?yšu)?ÔÂłő”Ä90%,ŁŹŽËr(shšȘ)ÄÁö(chšŁng)ÓÖÒ»ŽÎĐÔÔöŒÓÁË300Ö»ŃòĄŁ12ÌìșóÇàČʔĿÁżŚ?yšu)?ÔÂłő”Ä80%,ŁŹÈçčûÒȘŚÇàČĘÔÚœÓÏÂí(lšąi)4(gšš)ÔÂÈ(nšši)(ĂżÔ°Ž30ÌìÓ(jšŹ)Ëă)»Ű”œ3ÔÂłő”ÄżÁż,ŁŹtß@4(gšš)ÔÂégÔÄÁö(chšŁng)ÖÁ¶à·ĆÄÁ()Ö»ŃòĄŁ
A.800B.750
C.700D.600
ĄŸœâî}ˌ·Ąż
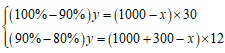
ÔO(shšš)ÄÁö(chšŁng)ÔÓĐČĘÁżéy,ŁŹČĘéL(zhšŁng)”ÄËÙ¶ÈéxĄŁÁĐ·œłÌœMŁș,ŁŹœâ”Ăx=800ŁŹy=60000,ĄŁ
ÔO(shšš)ÖÁ¶à·ĆÄÁNÖ»ŃòŁŹžùț(jšŽ)»Ű”œ3ÔÂłő”ÄżÁżÁĐ·œłÌŁș(100%-80%)y=(x-N)×120ŁŹŒŽ(100%-80%)×60000=(800-N)×120,ŁŹœâ”Ăn=700,ĄŁ
ÒòŽËŁŹßxńCßxí(xiš€ng),ĄŁ
Èę.č©ÇóÏà”È,ĄŁ
ß@·NÇér±ÈĘ^ș(jišŁn)ÎŁŹÖ»Đè°ŃÎŐŚĄÒ»(gšš)”ÈÁżêP(gušĄn)Ï”ŒŽN=xŒŽżÉ,ŁŹÔÚß@ÀïŸÍČ»ÔÙÙÊöÁË,ĄŁ
ÏàĐĆÍšß^(guš°)ß@ÆȘÎÄŐÂŁŹÍŹW(xušŠ)Š(dušŹ)ÓÚĆŁłÔČĘ(wššn)î}Ș(yš©ng)ÔÓĐÁËÒ»(gšš)Ę^éÇćÎú”ÄŐJ(rššn)ÖȘ,ŁŹœÓÏÂí(lšąi)Ö»ĐèÒȘÓĐáŠ(dušŹ)ĐÔ”ÄßM(jšŹn)ĐĐËąî}Ó(xšŽn)Ÿ,ŁŹŸÍÒ»¶šżÉÒÔÊìŸŐÆÎŐĄŁ
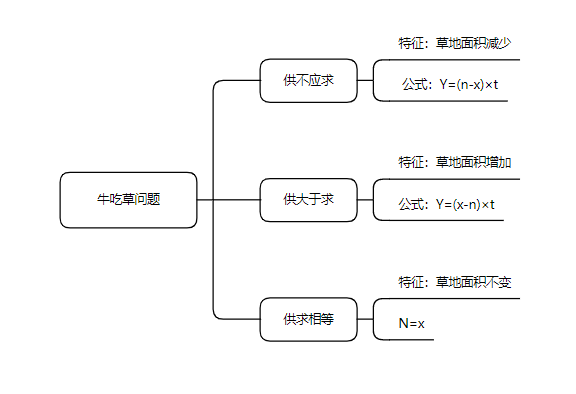

ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț
ÉÏÒ»ÆȘŁș2022ÊĄżŒĐĐy(cšš)ÙYÁÏ·ÖÎöÖĐ”ÄÔöéL(zhšŁng)ÂʱÈĘ^
ÏÂÒ»ÆȘŁș±Püc(dišŁn)2021ÄêÂ(lišąn)żŒÙYÁÏ·ÖÎö-ÔöéL(zhšŁng)ÂÊÏàêP(gušĄn)

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉż(jš©)ČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒ(wššn)Žđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé
”(shšŽ)ÁżêP(gušĄn)Ï”ŃÔŐZ(yšł)ÀíœâĆĐàÍÆÀíÙYÁÏ·ÖÎöłŁŚR(shšȘ)ĆĐàĐĐy(cšš)ŒŒÇÉ