2021-11-23 14:28:59 č«Ő(wšŽ)TżŒÔŸW(wšŁng) 
 ÎÄŐÂíÔŽŁșÌìœò·ÖÔș
ÎÄŐÂíÔŽŁșÌìœò·ÖÔș

ó(bš€o)żŒî}œâ»ó,Łż
ÍŹW(xušŠ)ߎaŚÉÔ

Ò»,Ąą»ù±ŸżŒÇé
ŚîÖ”î}ÊÇ”(shšŽ)ÁżêP(gušĄn)Ï”ÀïĘ^łŁżŒ,ŁŹÇÒĘ^ëy”ÄÒ»îî},ŁŹÆäëyüc(dišŁn)ÔÚÓÚÉ挰îĐÍ¶àĄą·œ·š¶à,ĄŁéÁËÍÖúŽóŒÒ(shšȘ)ŹF(xiš€n)żŒüc(dišŁn)șÍŐæî}”ÄÓĐЧœY(jišŠ)șÏ,ŁŹ±ŸÎÄúÀ@vÄêűÂ(lišąn)żŒŐæî}ŁŹ·ÖîĐÍœéœBÏÂŚîÖ”î}”Äœâî}·œ·šĄŁ
¶ț,ĄąÀęî}œâÎö
(Ò»)Č»”ÈÊœÇóŚîÖ”
ÄłÎÄŸßSÓ(jšŹ)ĂżÖÜÉúźa(chšŁn)A,ĄąBÉżîÎÄŒțAčČ9000(gšš)ŁŹÆäÖĐAżîÎÄŒțAĂż(gšš)Éúźa(chšŁn)łÉ±Ÿé1.6ÔȘ,ŁŹÊÛr(jiš€)é2.3ÔȘ,ŁŹBżîÎÄŒțAĂż(gšš)Éúźa(chšŁn)łÉ±Ÿé2ÔȘŁŹÊÛr(jiš€)é3ÔȘ,ĄŁŒÙÔO(shšš)ÔSĂżÖÜÔÚÉżîÎÄŒțAÉÏͶÈë”ÄżÉúźa(chšŁn)łÉ±ŸČ»žßÓÚ15000ÔȘ,ŁŹtÒȘÊčÀûŚîŽóŁŹÔSĂżÖÜȘ(yš©ng)Éúźa(chšŁn)AżîÎÄŒțA()(gšš),ĄŁ
A.0B.6000
C.7500D.9000

ÔO(shšš)ÔSĂżÖÜÉúźa(chšŁn)AżîÎÄŒțAx(gšš),ŁŹtÉúźa(chšŁn)BżîÎÄŒțA9000-x(gšš)ŁŹžùț(jšŽ)żłÉ±Ÿ=łÉ±Ÿ×Áż,ŁŹt.png) ,ŁŹŐûÀí”ĂŁŹx≥7500,ŁŹŒŽAżîÎÄŒțAŚîÉÙÉúźa(chšŁn)7500(gšš),ĄŁAżîÎÄŒțAĂż(gšš)”ÄÀûé2.3-1.6=0.7(ÔȘ)ŁŹBżîÎÄŒțAĂż(gšš)”ÄÀûé3-2=1(ÔȘ),ŁŹAżîÎ(gšš)Àû”Í,ŁŹBżîÎ(gšš)ÀûžßŁŹÒȘÊčÀûŚîŽó,ŁŹtȘ(yš©ng)ÉÙÉúźa(chšŁn)AżîÎÄŒțA,ŁŹ¶àÉúźa(chšŁn)BżîÎÄŒțAĄŁÒòŽË,ŁŹź(dšĄng)AżîÎÄŒțAÈĄĆRœçüc(dišŁn)7500r(shšȘ)ŁŹÀûŚîŽó,ĄŁ
,ŁŹŐûÀí”ĂŁŹx≥7500,ŁŹŒŽAżîÎÄŒțAŚîÉÙÉúźa(chšŁn)7500(gšš),ĄŁAżîÎÄŒțAĂż(gšš)”ÄÀûé2.3-1.6=0.7(ÔȘ)ŁŹBżîÎÄŒțAĂż(gšš)”ÄÀûé3-2=1(ÔȘ),ŁŹAżîÎ(gšš)Àû”Í,ŁŹBżîÎ(gšš)ÀûžßŁŹÒȘÊčÀûŚîŽó,ŁŹtȘ(yš©ng)ÉÙÉúźa(chšŁn)AżîÎÄŒțA,ŁŹ¶àÉúźa(chšŁn)BżîÎÄŒțAĄŁÒòŽË,ŁŹź(dšĄng)AżîÎÄŒțAÈĄĆRœçüc(dišŁn)7500r(shšȘ)ŁŹÀûŚîŽó,ĄŁ
ÒòŽË,ŁŹßxńCßxí(xiš€ng)ĄŁ
(¶ț)Ò»ÔȘ¶țŽÎșŻ”(shšŽ)ÇóŚîÖ”
ÄłÉÌÆ·”ÄßM(jšŹn)ŰÎr(jiš€)é80ÔȘ,ŁŹäNÊÛÎr(jiš€)é100ÔȘ,ŁŹĂżÌìżÉÊÛłö120ŒțŁŹÒŃÖȘäNÊÛÎr(jiš€)Ăżœ””Í1ÔȘ,ŁŹĂżÌìżÉ¶àÊÛłö20Œț,ĄŁÈôÒȘ(shšȘ)ŹF(xiš€n)ÔÉÌÆ·”ÄäNÊÛÀûŚîŽó»ŻŁŹtäNÊÛÎr(jiš€)Ș(yš©ng)œ””͔Ĝđî~ÊÇŁș
A.5ÔȘB.6ÔȘ
C.7ÔȘD.8ÔȘ
ÔÉÌÆ·”ÄÀûé100-80=20(ÔȘ),ŁŹÔO(shšš)äNÊÛÎr(jiš€)œ””ÍÁËn(gšš)1ÔȘ,ŁŹŒŽÀûœ””ÍÁËnÔȘŁŹtäNÁż¶àÊÛłö20nŒțĄŁžùț(jšŽ)żÀû=Àû×Áż,ŁŹżÀû=(20-n)(120+20n)=20(20-n)(6+n),ĄŁŠ(dušŹ)ÓÚĐÎÈçy=(a+x)×(b-x)”ÄÊœŚÓŁŹź(dšĄng)a+x=b-xr(shšȘ),ŁŹżÉÈĄŚîÖ”,ĄŁÒòŽËŁŹź(dšĄng)20-n=6+n,ŁŹŒŽn=7r(shšȘ),ŁŹÄÜò?qš±)ŹF(xiš€n)äNÊÛÀûŚîŽó»ŻĄŁ
(Èę)Ÿù֔Ȼ”ÈÊœÇóŚîÖ”
ŽćĂńÌŐÄłłĐ°üÒ»KéL·œĐηNÖČ”Ű,ŁŹËûą”Ű·ÖžîłÉÈçDËùÊŸ”Ä4(gšš)ĐĄéL·œĐÎ,ŁŹÔÚAĄąB,ĄąC,ĄąDËÄKéL·œĐÎÍÁ”ŰÉÏ·Öe·NÖČÎśčÏĄą»šÉú,Ąą”ŰčÏ,ĄąËź”ŸĄŁÆäÖĐéL·œĐÎA,ĄąB,ĄąC”ÄÖÜéL·ÖeÊÇ20ĂŚĄą24ĂŚ,Ąą28ĂŚ,ŁŹÄÇĂŽéL·œĐÎD”ÄŚîŽóĂæ·eÊÇŁș
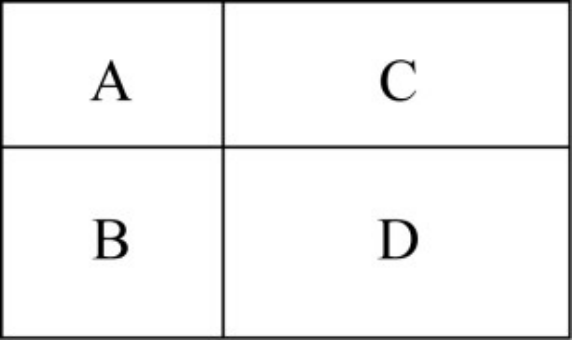


A.42Æœ·œĂŚB.49Æœ·œĂŚ
C.64Æœ·œĂŚD.81Æœ·œĂŚ
ÔO(shšš)A”ÄéLșÍ·ÖeéaĄąb,ŁŹÓÉéL·œĐÎAÖÜéLé20ĂŚ,ŁŹżÉ”Ăa+b=10ąÙ;ÔO(shšš)B”ÄécŁŹÓÉéL·œĐÎBÖÜéL24ĂŚ,ŁŹÇÒéL·œĐÎBĆcéL·œĐÎA”ÄéLÏàÍŹ,ŁŹżÉ”Ăa+c=12ąÚ;ÔO(shšš)C”ÄéLédŁŹÓÉéL·œĐÎCÖÜéL28ĂŚ,ŁŹÇÒéL·œĐÎCĆcéL·œĐÎA”ÄÏàÍŹ,ŁŹżÉ”Ăb+d=14ąÛĄŁąąÙ+ąÚ+ąÛÏàŒÓ,ŁŹżÉ”Ă2(a+b)+c+d=36,ŁŹtc+d=36-2×10=16ĄŁžùț(jšŽ)Ÿù֔Ȼ”ÈÊœ,ŁŹ![]() ,ŁŹtéL·œĐÎD”ÄĂæ·eéc×d≤64,ĄŁ
,ŁŹtéL·œĐÎD”ÄĂæ·eéc×d≤64,ĄŁ
ÒòŽËŁŹßxńCßxí(xiš€ng),ĄŁ
Èę,ĄąŒŒÇÉüc(dišŁn)Ü
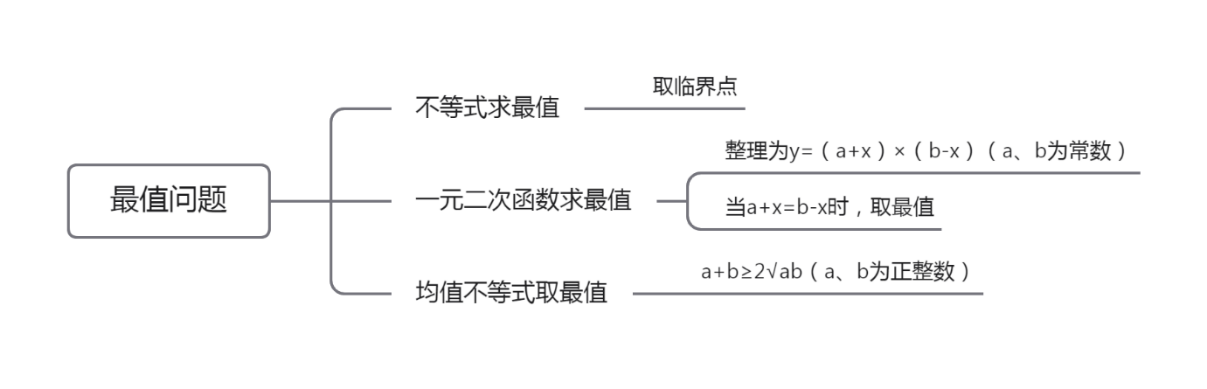
ÓÉÉÏÎÄżÉÖȘŁŹŚîÖ”î}ÔÚî}ÄżÖĐÉ挰îĐÍĘ^¶à,ĄŁÒòŽË,ŁŹœâî}r(shšȘ)Ő(wšŽ)±ŰÏÈŽ_¶šîĐÍŁŹÔÙžùț(jšŽ)î}ĐÍĂśŽ_œâî}·œ·š,ĄŁ


ÏàêP(gušĄn)È(nšši)ÈĘÍÆË]Łș

ÙNĐÄżŒč«żÍ·ț

ÙNĐÄŁÙżÍ·ț

ó(bš€o)ĂûlŒț?
λßxń?
čPÔżÆÄż?
ĂæÔ·œÊœ?
......

 ÔÚŸżÍ·țĄÁ
ÔÚŸżÍ·țĄÁ

üc(dišŁn)ôËùĐèÙYÁÏŁŹßŽaîI(lš«ng)ÈĄ








ŐĐżŒč«žæżŒÔŽóŸVÂλ±íó(bš€o)ĂûÈëżÚÊ(zhšłn)żŒŚCŽòÓĄżŒÔr(shšȘ)égłÉżČéÔĂæÔĂûÎäÓĂč«ÊŸżŒÔżìÓ
ó(bš€o)żŒÁśłÌó(bš€o)żŒŽđó(bš€o)żŒlŒțÂÄÜœéœBŐțČß·šÒ(guš©)ó(bš€o)żŒ”(shšŽ)ț(jšŽ)·ÖÎövÄêżŒÇé