2021-06-04 09:25:22 №«„Х(wЁҙ)ҶTҝјФҮҫW(wЁЈng) 
 ОДХВҒнФҙЈәәУұұ·ЦФә
ОДХВҒнФҙЈәәУұұ·ЦФә
ЎЎЎЎёЕВКҶ–о}ҺЧәхКЗҮшјТ№«„Х(wЁҙ)ҶTҝјФҮөДұШҝјо}ЎЈГжҢҰо}БҝҫЮҙуөДРРңyҝјФҮЈ¬•rйg·ЦЕдФЪҙро}Я^іМЦРЦБкP(guЁЎn)ЦШТӘ,Ј¬ТтҙЛҢҰУЪЯ@·NұШҝјо},Ј¬ҝјЙъӮғҝЙТФМбЗ°ңКӮдЈ¬ҙуБҝЛўо}·eАЫҪӣ(jЁ©ng)тһ,Ј¬ҝјФҮЯ^іМЦР,Ј¬ҪY(jiЁҰ)әПКЈУаҝјФҮ•rйgСёЛЩЕР”аКЗ·сЧчҙрТФј°Ччҙр•rІЙУГөДҪво}·Ҫ·ЁЎЈ
ЎЎЎЎёЕВКҶ–о}о}РНҙуЦВ·ЦһйғЙ·N,Ј¬Т»оҗКЗГиКцКВјюРН,Ј¬Т»оҗКЗТСЦӘёЕВКРНЈ¬Ждлy¶Иёч®җ,Ј¬ҝЙ…ўҝјПВБРҢ§ҲDЈә
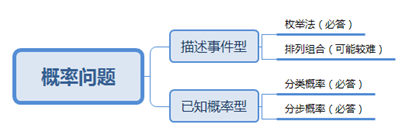
ЎЎЎЎТ»,ЎўГиКцКВјюРН
ЎЎЎЎГиКцКВјюРНөДёЕВКҶ–о}НЁіЈЦ»РиМЧУГ№«КҪЈ¬ёЕВК ,Ј¬Йжј°өҪ”ө(shЁҙ)”ө(shЁҙ)·Ҫ·ЁНЁіЈЙжј°өҪГ¶ЕeәНЕЕБРҪMәП,Ј¬ИзАэ1ЎЈ
,Ј¬Йжј°өҪ”ө(shЁҙ)”ө(shЁҙ)·Ҫ·ЁНЁіЈЙжј°өҪГ¶ЕeәНЕЕБРҪMәП,Ј¬ИзАэ1ЎЈ
ЎЎЎЎЎҫАэ1Ўҝ(2017Үшҝј)ДіҙОЦӘЧRёӮЩҗФҮҫн°ьАЁ3өАГҝо}10·ЦөДјЧоҗо},Ј¬2өАГҝо}20·ЦөДТТоҗо}ТФј°1өА30·ЦөДұыоҗо},ЎЈ…ўЩҗХЯЪwДілSҷCЯx“сЖдЦРөДІҝ·ЦФҮо}ЧчҙрІўИ«ІҝҙрҢҰЈ¬ЖдЧоҪKөГ·Цһй70·Ц,ЎЈҶ–ЪwДіОҙЯx“сұыоҗо}өДёЕВКһй¶аЙЩ?

ЎЎЎЎЎҫЛјВ·ТэҢ§ЎҝҙЛо}һйёЕВКҶ–о}ГиКцКВјюРН,Ј¬РиУГ№«КҪУӢЛгЈ¬ХТөҪҝӮөДКВјю”ө(shЁҙ)әНқMЧг—lјюөДКВјю”ө(shЁҙ),ЎЈЧоҪK·Ц”ө(shЁҙ)һй70·Ц,Ј¬УГГ¶Еe·ЁТ»Т»БРЕeҝЙДЬРФһйўЩ1өАұыоҗо}Ј¬2өАТТоҗо},Ј¬№І1·N·Ҫ·Ё;ўЪ1өАұыоҗо},Ј¬1өАТТоҗо}Ј¬2өАјЧоҗо},Ј¬№І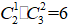 ·N·Ҫ·Ё;ўЫ2өАТТоҗо},Ј¬3өАјЧоҗо}Ј¬№І1·N·Ҫ·Ё,ЎЈТтҙЛҝӮөДКВјю”ө(shЁҙ)һй8·N,Ј¬қMЧг—lјюөДКВјю”ө(shЁҙ)ғH1·NЈ¬ҙъИ빫КҪp=
·N·Ҫ·Ё;ўЫ2өАТТоҗо},Ј¬3өАјЧоҗо}Ј¬№І1·N·Ҫ·Ё,ЎЈТтҙЛҝӮөДКВјю”ө(shЁҙ)һй8·N,Ј¬қMЧг—lјюөДКВјю”ө(shЁҙ)ғH1·NЈ¬ҙъИ빫КҪp= ,Ј¬Яx“сDЯxн—,ЎЈҙЛо}ғHУГГ¶Еe·ЁәНәҶҶОЕЕБРҪMәПөДЦӘЧRҫНДЬЗуҪвіцҒнЈ¬лy¶ИІ»ҙу,Ј¬”ө(shЁҙ)ұШҙро},ЎЈ
,Ј¬Яx“сDЯxн—,ЎЈҙЛо}ғHУГГ¶Еe·ЁәНәҶҶОЕЕБРҪMәПөДЦӘЧRҫНДЬЗуҪвіцҒнЈ¬лy¶ИІ»ҙу,Ј¬”ө(shЁҙ)ұШҙро},ЎЈ
ЎЎЎЎ¶ю,ЎўТСЦӘёЕВКРН
ЎЎЎЎТСЦӘёЕВКРНөДёЕВКҶ–о}НЁіЈЦұҪУҪoіц»тйgҪУЗуөГёЕВКЈ¬І»ұШУГ№«КҪУӢЛг,Ј¬ҝјІйөДКЗёЕВКЕcјУ·ЁФӯАнәНіЛ·ЁФӯАнөДҪY(jiЁҰ)әП,Ј¬јҙ·ЦоҗёЕВКәН·ЦІҪёЕВКЎЈИз№ыЛщЗуКВјюһйІўБРкP(guЁЎn)Пө,Ј¬„tҢўёчІҝ·ЦёЕВКјУФЪТ»Жр,Ј¬Из№ыЛщЗуКВјюһй·ЦІҪНкіЙЈ¬ГҝӮҖІҪуE¶јКЗұШІ»ҝЙЙЩөД,Ј¬„tҢўёчІҝ·ЦёЕВКіЛФЪТ»Жр,Ј¬ИзАэ2ЎЈ
ЎЎЎЎЎҫАэ2Ўҝ(2019Үшҝј)јЧәНТТЯMРР5ҫЦ3„ЩөДЖ№ЕТЗтұИЩҗ,Ј¬јЧГҝҫЦ«@„ЩөДёЕВККЗТТГҝҫЦ«@„ЩёЕВКөД1.5ұ¶,ЎЈҶ–ТФПВДД·NЗйӣr°l(fЁЎ)ЙъөДёЕВКЧоҙу?
ЎЎЎЎA. ұИЩҗФЪ3ҫЦғИ(nЁЁi)ҪY(jiЁҰ)Кш B. ТТЯB„Щ3ҫЦ«@„Щ
ЎЎЎЎC. јЧ«@„ЩЗТғЙИЛҫщҹoЯB„Щ D. ТТУГ4ҫЦ«@„Щ
ЎЎЎЎЎҫЛјВ·ТэҢ§ЎҝҙЛо}һйёЕВКҶ–о}ТСЦӘёЕВКРНЈ¬јЧТТ«@„ЩөДёЕВКЦ®әНһй1,Ј¬һйҝЙУЙ“јЧГҝҫЦ«@„ЩөДёЕВККЗТТГҝҫЦ«@„ЩёЕВКөД1.5ұ¶”ЗуіцјЧ«@„ЩёЕВКһй0.6,Ј¬ТТ«@„ЩёЕВКһй0.4ЎЈAЯxн—,Ј¬ұИЩҗФЪ3ҫЦғИ(nЁЁi)ҪY(jiЁҰ)Кш,Ј¬„tјЧЯB„ЩИэҫЦ»тТТЯB„ЩИэҫЦЈ¬јЧ„ЩТ»ҫЦёЕВКһй0.6,Ј¬ЯB„ЩИэҫЦ,Ј¬ГҝҫЦұШҙтЈ¬ёЕВКПаіЛ,Ј¬ТтҙЛһй0.6×0.6×0.6Ј¬Н¬Ан,Ј¬ТТЯB„ЩИэҫЦёЕВКһй0.4×0.4×0.4,Ј¬ғЙХЯһйІўБРкP(guЁЎn)ПөЈ¬ТтҙЛұИЩҗФЪ3ҫЦғИ(nЁЁi)ҪY(jiЁҰ)Кш,Ј¬ҢўғЙІҝ·ЦёЕВКјУФЪТ»Жр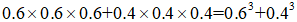 ;BЯxн—,Ј¬ТТЯB„Щ3ҫЦЈ¬ҝЙДЬКЗЗ°ИэҫЦТТИ«„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй0.4×0.4×0.4,Ј¬ҝЙДЬКЗөЪТ»ҫЦТТЭ”,Ј¬ФЩЯB„Щ3ҫЦЈ¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛ,Ј¬һй0.6×0.4×0.4×0.4,Ј¬ЯҖҝЙДЬЗ°ғЙҫЦТТЭ”Ј¬әуИэҫЦТТ„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй0.6×0.6×0.4×0.4×0.4,Ј¬Иэ·NҝЙДЬРФІўБРкP(guЁЎn)Пө,Ј¬јУФЪТ»Жрһй
;BЯxн—,Ј¬ТТЯB„Щ3ҫЦЈ¬ҝЙДЬКЗЗ°ИэҫЦТТИ«„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй0.4×0.4×0.4,Ј¬ҝЙДЬКЗөЪТ»ҫЦТТЭ”,Ј¬ФЩЯB„Щ3ҫЦЈ¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛ,Ј¬һй0.6×0.4×0.4×0.4,Ј¬ЯҖҝЙДЬЗ°ғЙҫЦТТЭ”Ј¬әуИэҫЦТТ„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй0.6×0.6×0.4×0.4×0.4,Ј¬Иэ·NҝЙДЬРФІўБРкP(guЁЎn)Пө,Ј¬јУФЪТ»Жрһй Ј¬РЎУЪAЯxн—,Ј¬;CЯxн—,Ј¬јЧ«@„ЩЗТғЙИЛҫщҹoЯB„ЩЈ¬Ц»ДЬКЗјЧ„ЩТТ„ЩјЧ„ЩТТ„ЩјЧ„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй
Ј¬РЎУЪAЯxн—,Ј¬;CЯxн—,Ј¬јЧ«@„ЩЗТғЙИЛҫщҹoЯB„ЩЈ¬Ц»ДЬКЗјЧ„ЩТТ„ЩјЧ„ЩТТ„ЩјЧ„Щ,Ј¬ГҝҫЦұШҙт,Ј¬ёЕВКПаіЛЈ¬һй ,Ј¬РЎУЪAЯxн—,Ј¬DЯxн—Ј¬ТТУГ4ҫЦ«@„Щ,Ј¬„tЗйӣrһйЗ°3ҫЦТТ„Щ2ҫЦ,Ј¬ЧоәуТ»ҫЦһйТТ„ЩЈ¬ГҝҫЦұШҙт,Ј¬ёЕВКһй
,Ј¬РЎУЪAЯxн—,Ј¬DЯxн—Ј¬ТТУГ4ҫЦ«@„Щ,Ј¬„tЗйӣrһйЗ°3ҫЦТТ„Щ2ҫЦ,Ј¬ЧоәуТ»ҫЦһйТТ„ЩЈ¬ГҝҫЦұШҙт,Ј¬ёЕВКһй ,Ј¬РЎУЪAЯxн—ЎЈТтҙЛҙр°ёһйAЯxн—,ЎЈҙЛо}ЦчТӘҝјІй·ЦоҗёЕВКәН·ЦІҪёЕВКөД‘ӘУГ,Ј¬ҝјФҮТ»¶ЁТӘ·ЦЗеКІГҙ•rәтУГјУ·ЁКІГҙ•rәтУГіЛ·ЁЎЈ
,Ј¬РЎУЪAЯxн—ЎЈТтҙЛҙр°ёһйAЯxн—,ЎЈҙЛо}ЦчТӘҝјІй·ЦоҗёЕВКәН·ЦІҪёЕВКөД‘ӘУГ,Ј¬ҝјФҮТ»¶ЁТӘ·ЦЗеКІГҙ•rәтУГјУ·ЁКІГҙ•rәтУГіЛ·ЁЎЈ
ЎЎЎЎҝӮЦ®,Ј¬ҢҰУЪёЕВКҶ–о},Ј¬КЧПИРиТӘОТӮғҪY(jiЁҰ)әПҝјФҮ•rйgҝмЛЩЕР”аКЗ·сЯMРРЧчҙрЈ¬ЯM¶шСёЛЩҙ_¶ЁҪво}·Ҫ·Ё,Ј¬ЦрІҪН»ЖЖ,ЎЈПаРЕёчО»ҝјЙъҪӣ(jЁ©ng)Я^ҙуБҝҫҡБ•Ј¬Я@оҗо}РНұШДЬКЦөҪЗЬҒн,ЎЈ

ПакP(guЁЎn)ғИ(nЁЁi)ИЭНЖЛ]Јә

ЩNРДҝј№«ҝН·ю

ЩNРДҢЈҢЩҝН·ю

ҲуГы—lјю?
ҚҸО»Яx“с?
№PФҮҝЖДҝ?
ГжФҮ·ҪКҪ?
......

 ФЪҫҖҝН·юЎБ
ФЪҫҖҝН·юЎБ

ьc“фЛщРиЩYБП,Ј¬’ЯҙaоI(lЁ«ng)ИЎ








ХРҝј№«ёжҝјФҮҙуҫVВҡО»ұнҲуГыИлҝЪңКҝјЧCҙтУЎҝјФҮ•rйgіЙҝғІйФғГжФҮГыҶОдӣУГ№«КҫҝјФҮҝмУҚ